
35.Сущность акф
Автокорреляционная функция - это характеристика сигнала, которая помогает находить повторяющиеся участки сигнала или определять несущую частотусигнала, скрытую из-за наложений шума и колебаний на других частотах. Автокорреляционная функция часто используется вобработке сигналови анализевременных рядов.
Автокорреляционная
функция сигнала с конечной энергией –
это значение интеграла от произведения
двух копий этого сигнала, сдвинутых
относительно друг друга на время τ,
рассматриваемое в функции этого
временного сдвига τ: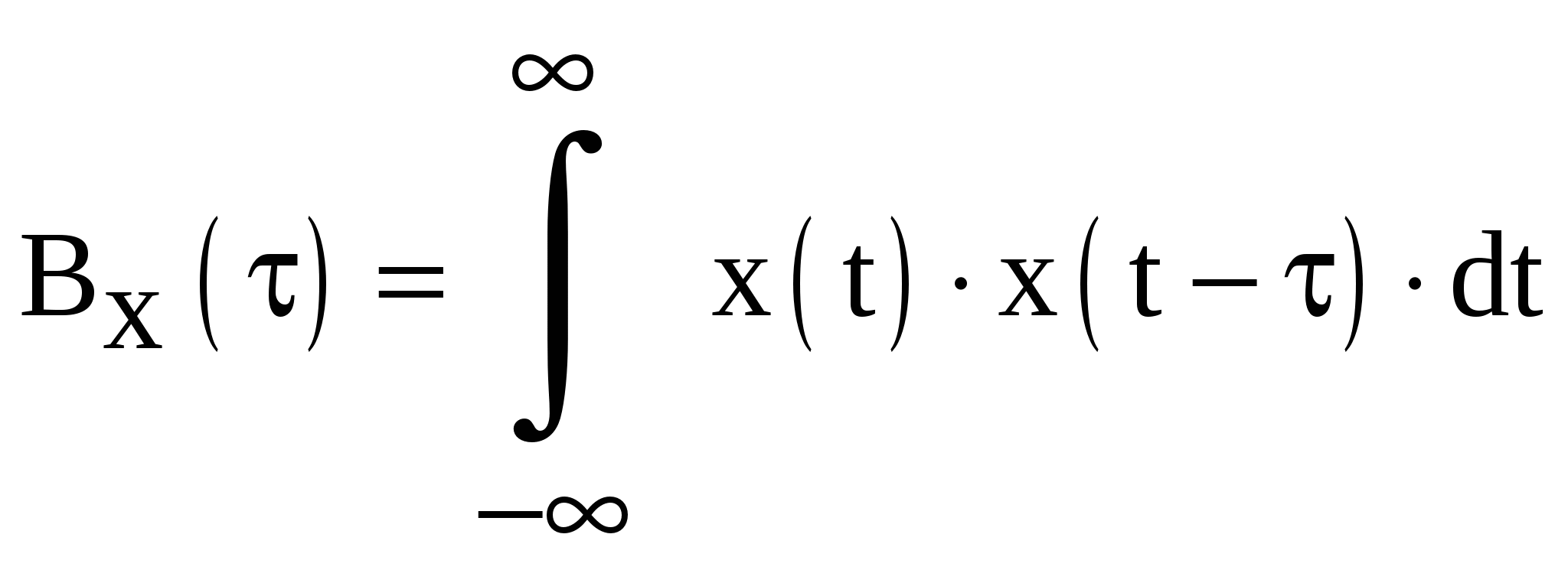
36.Периодичная функция с помощью ряда Котельникова
Аналитическое значение ряда Котельникова для сигнала S(t) записывается как:
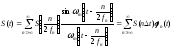
где n - номер выборки.
37. ВКФ и ее свойства


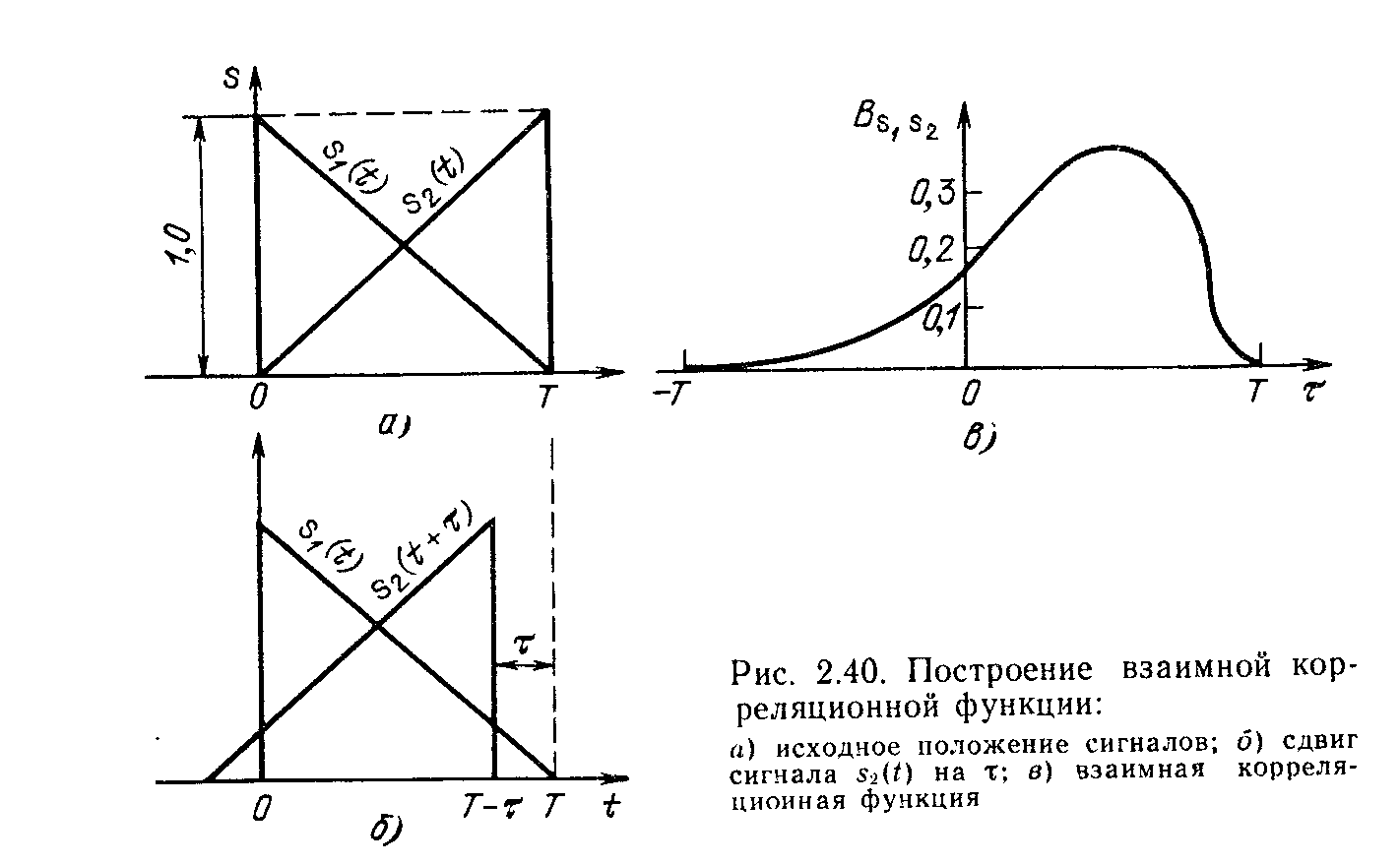
38. Спектр прямоугольного сигнала
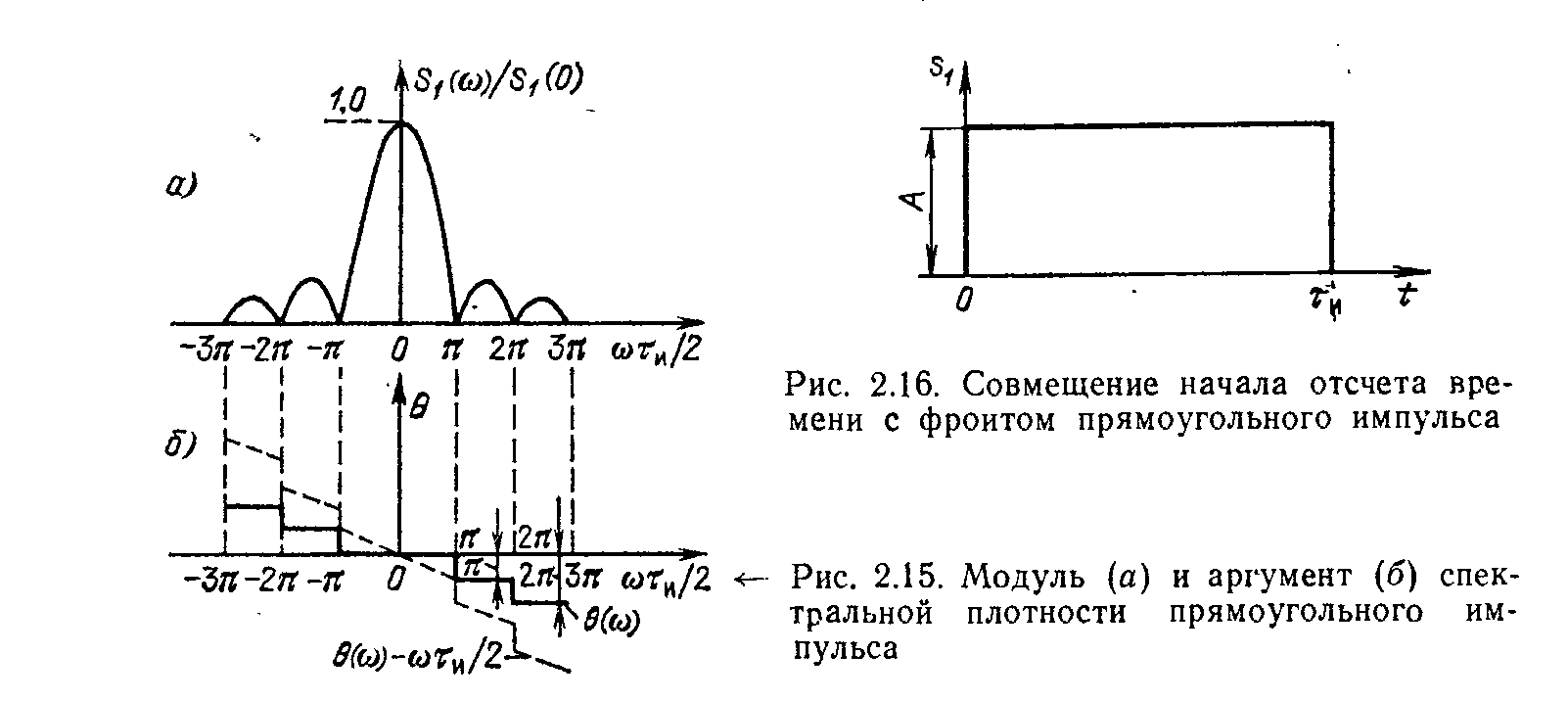
39. Выбор шага дискретизации


40. Формула спектральной плотности
![]()
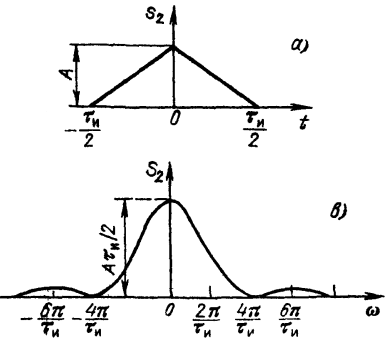
41. Спектр треугольного импульса
Импульс:
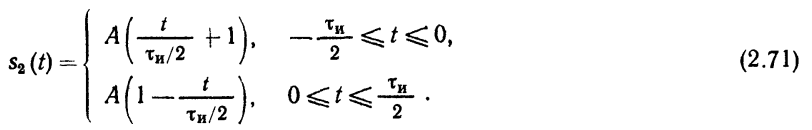
Спектральная плотность импульса:
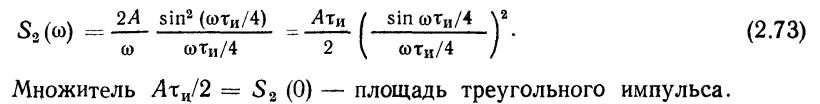
График импульса и спектральной плоскости:
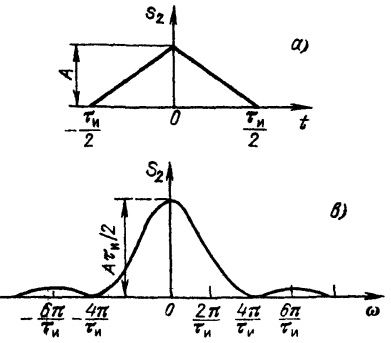
42. Спектр пачки импульсов

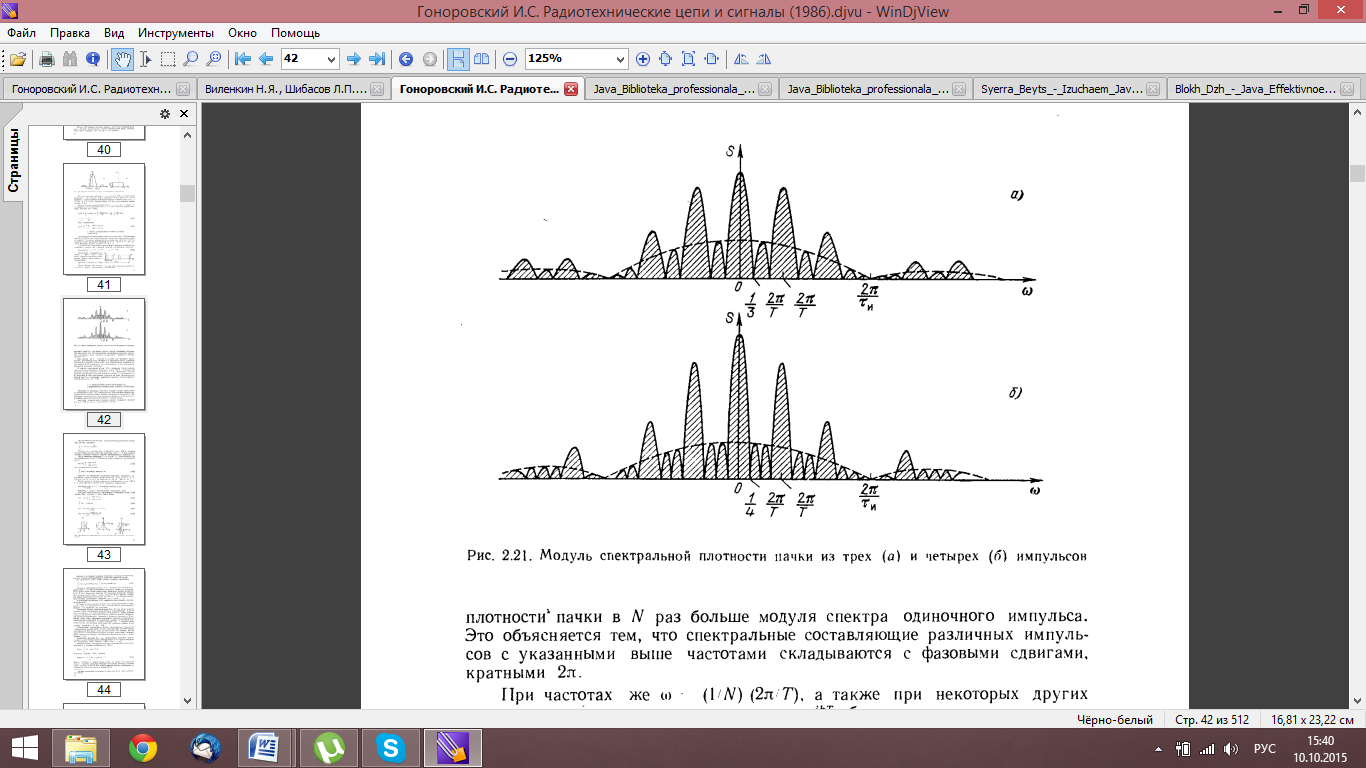
43. Представление дискретизируемого сигнала во временной и частотной области
Во временной:
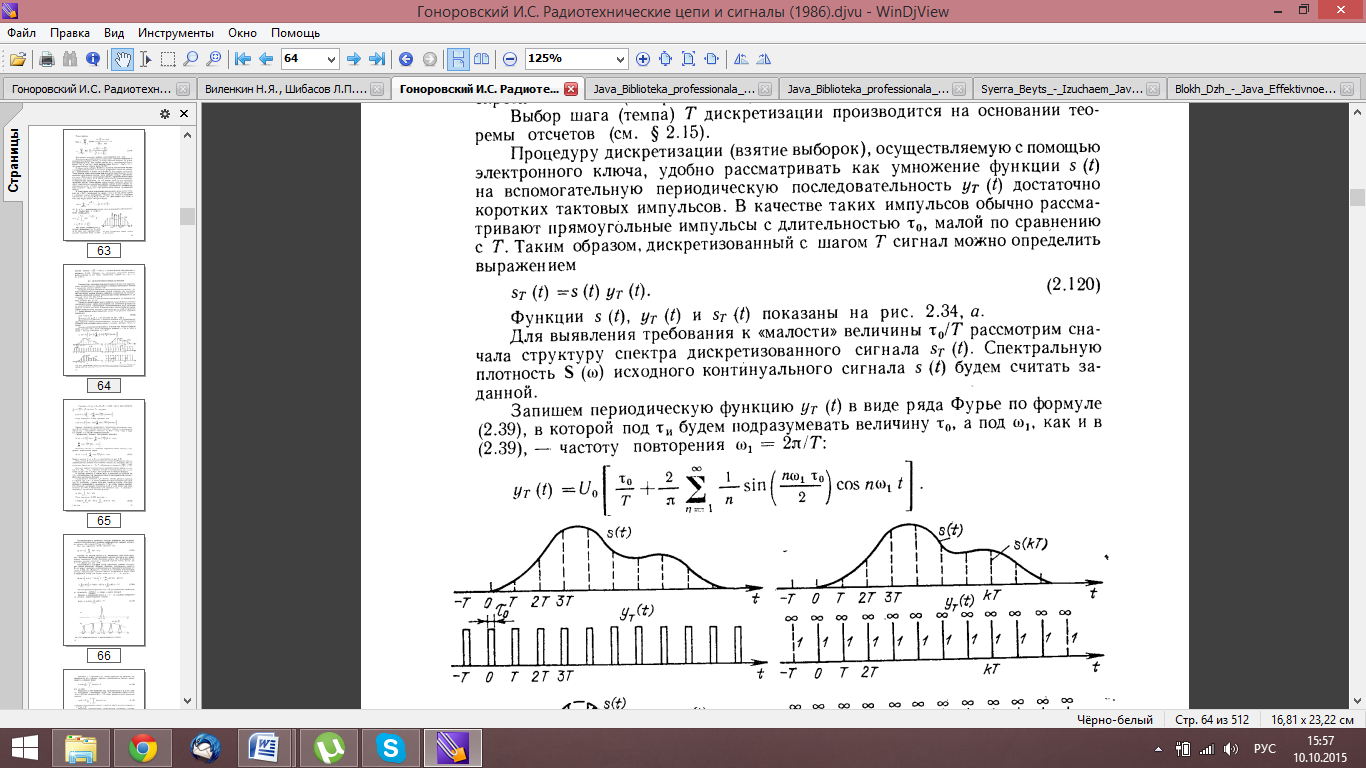
В частотной области:
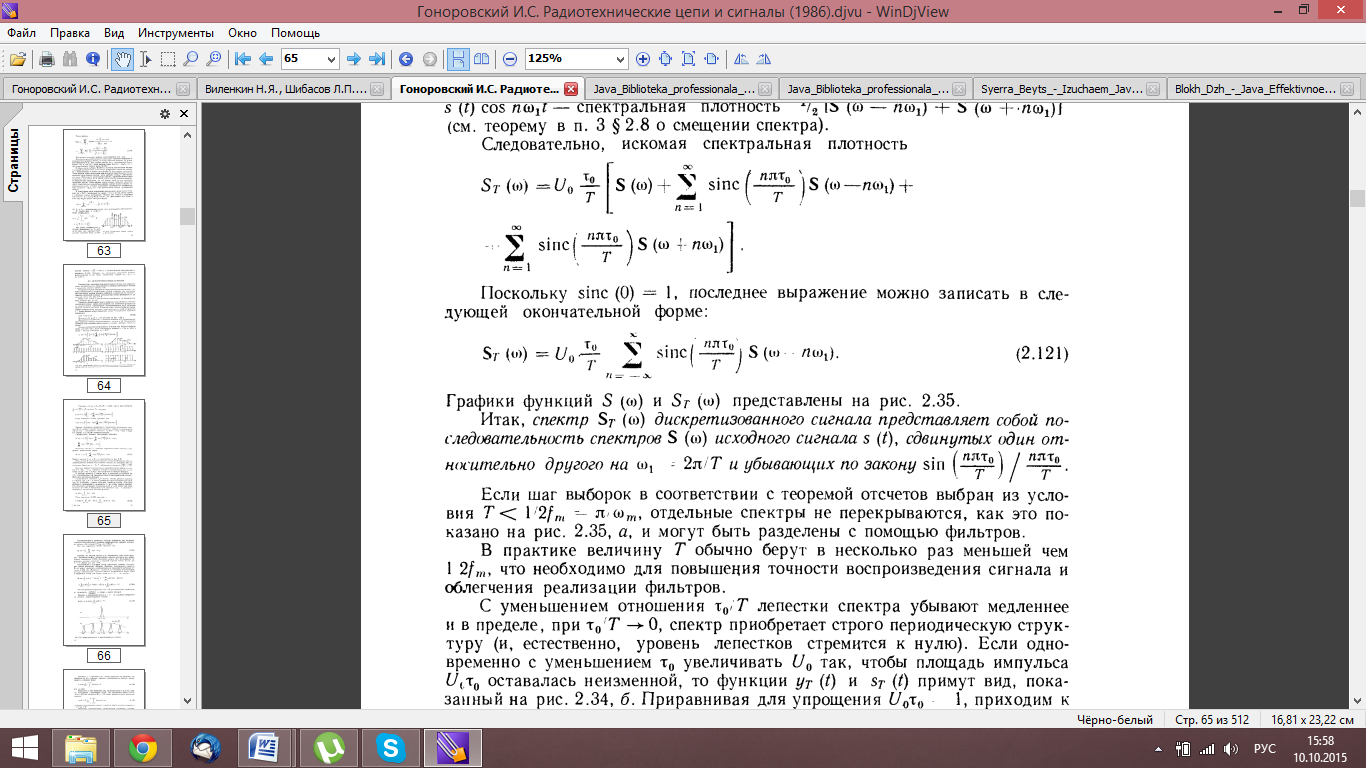
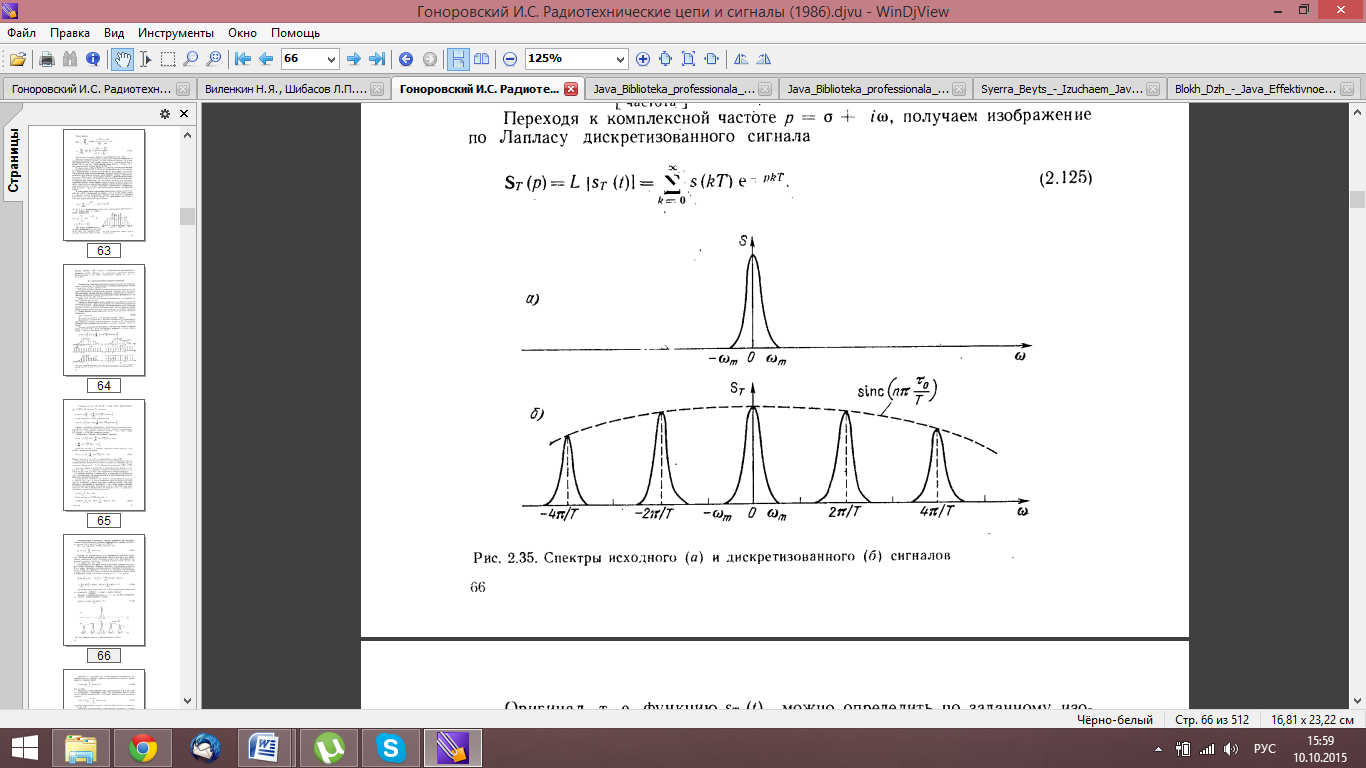
44. АКФ непериодического сигнала
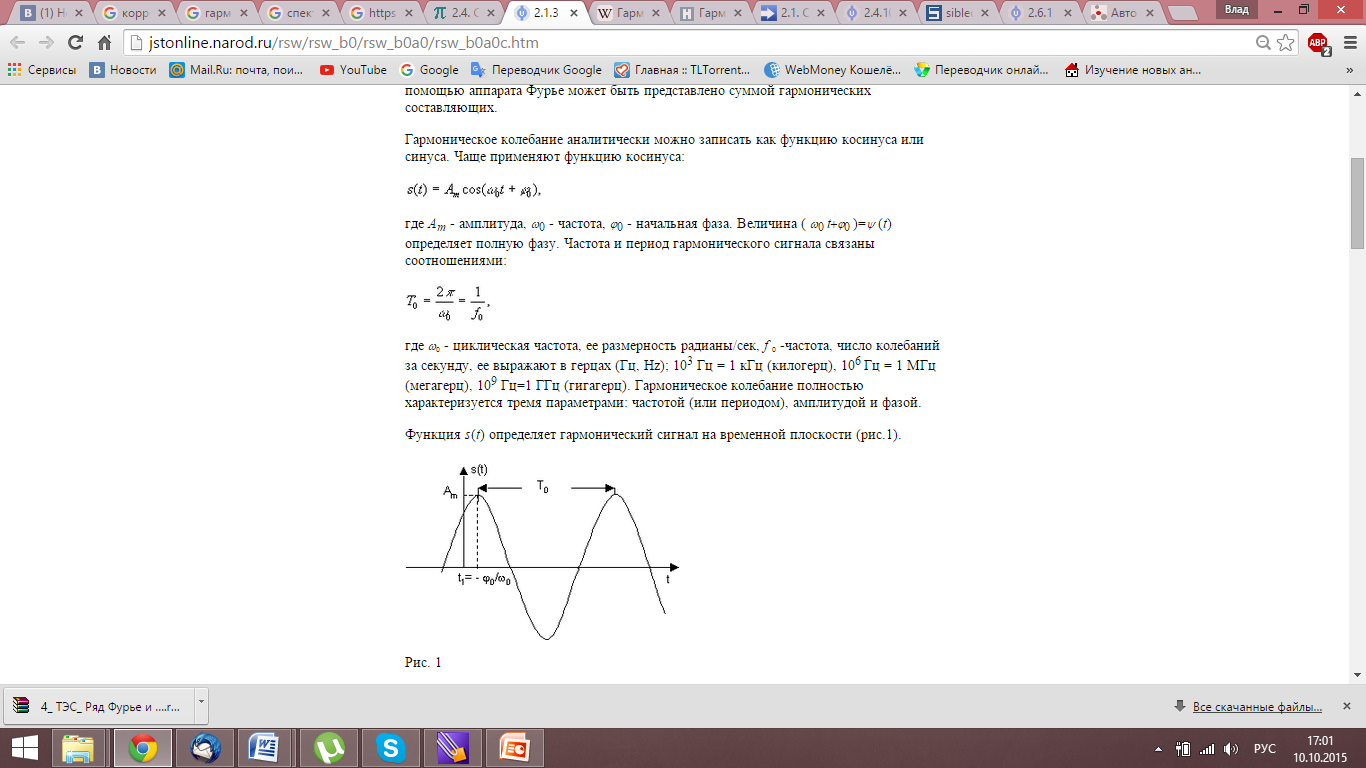
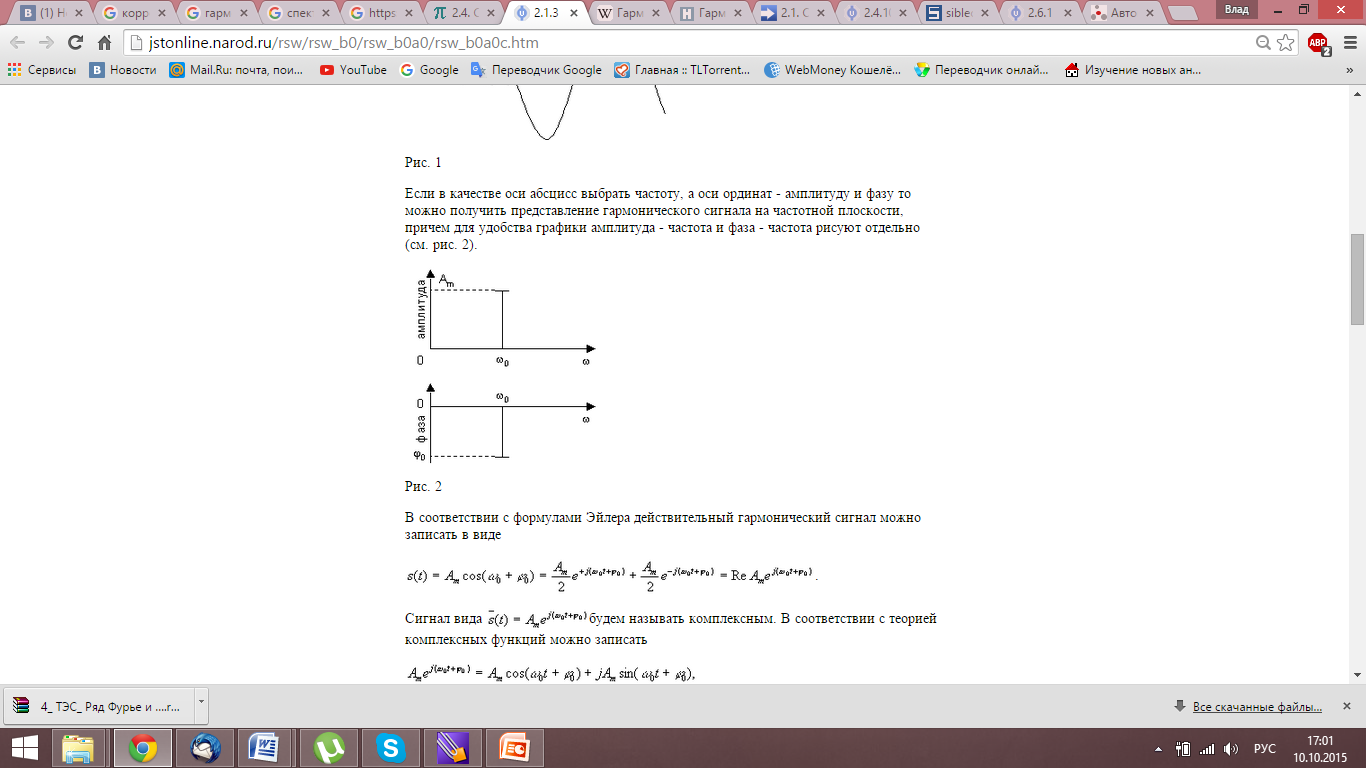
45. Спектральная плотность гармонического сигнала
46. АКФ периодического сигнала
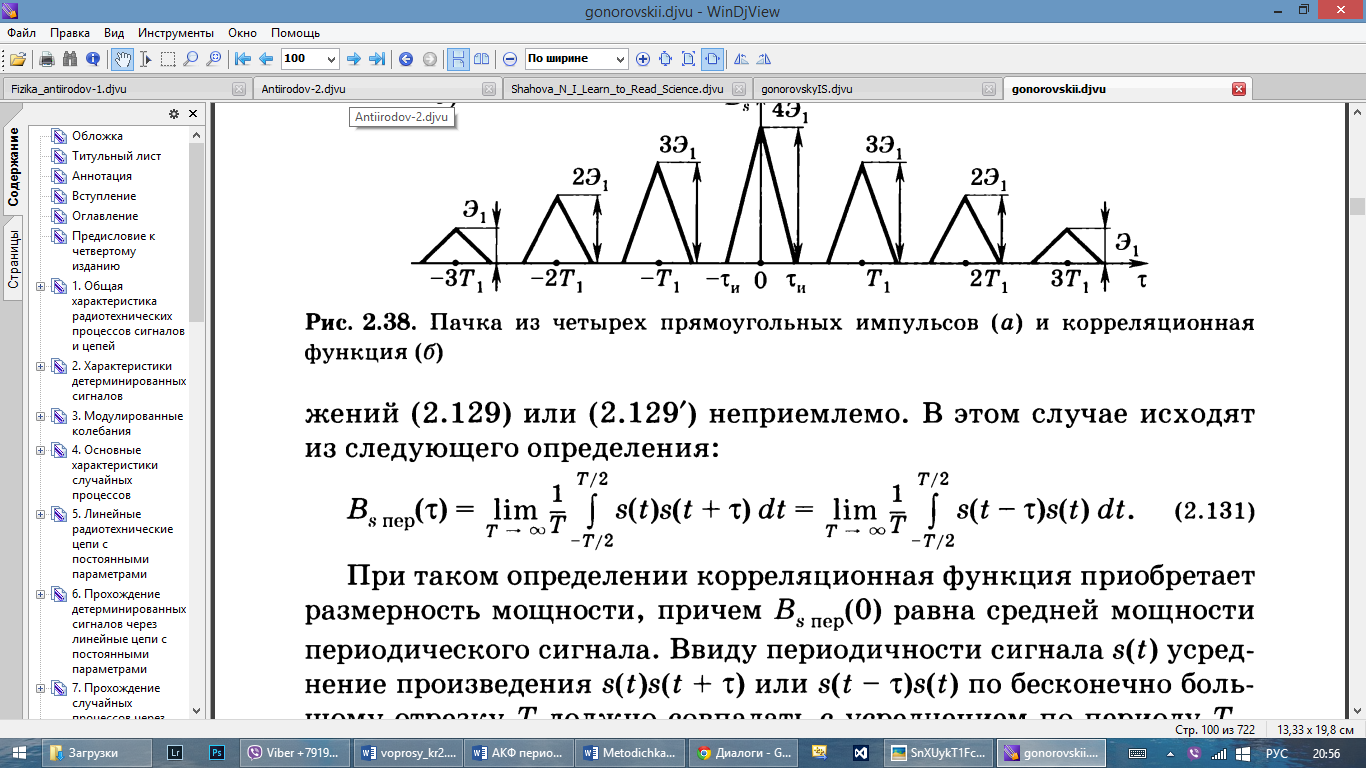
При
таком определении корреляционная ф-ия
приобретает размерность мощности,
причем при
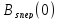 равна средней мощности периодического
сигнала.
равна средней мощности периодического
сигнала.
47. Единичный импульс и его спектр

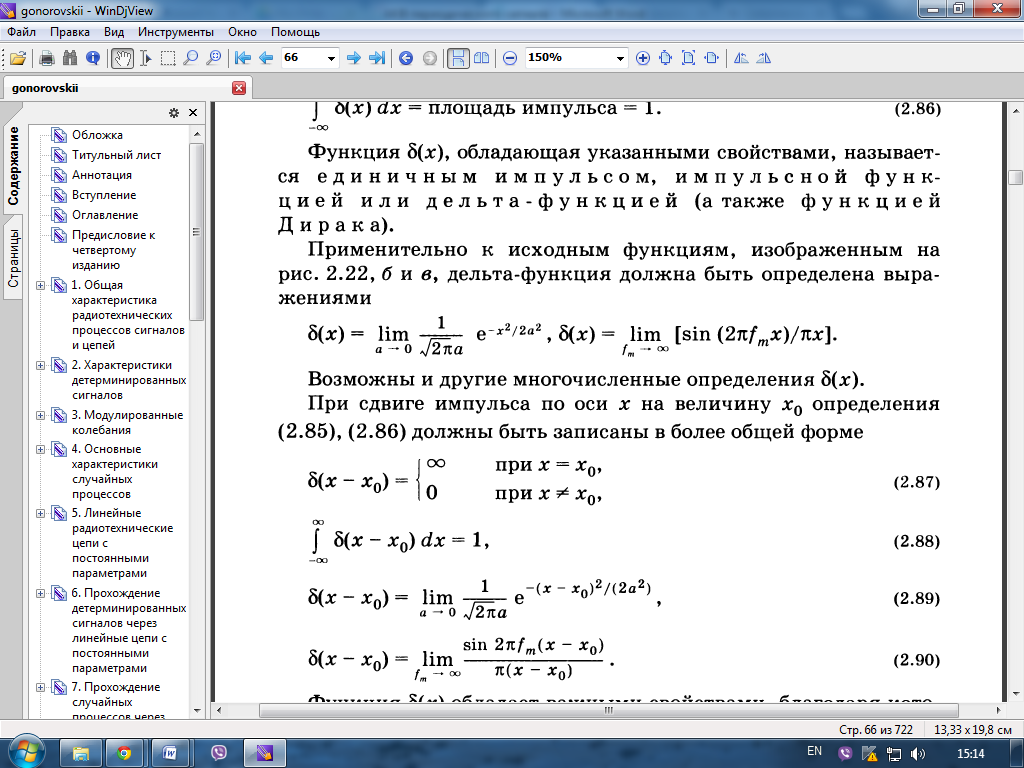
Фильтрующее
св-во:![]()
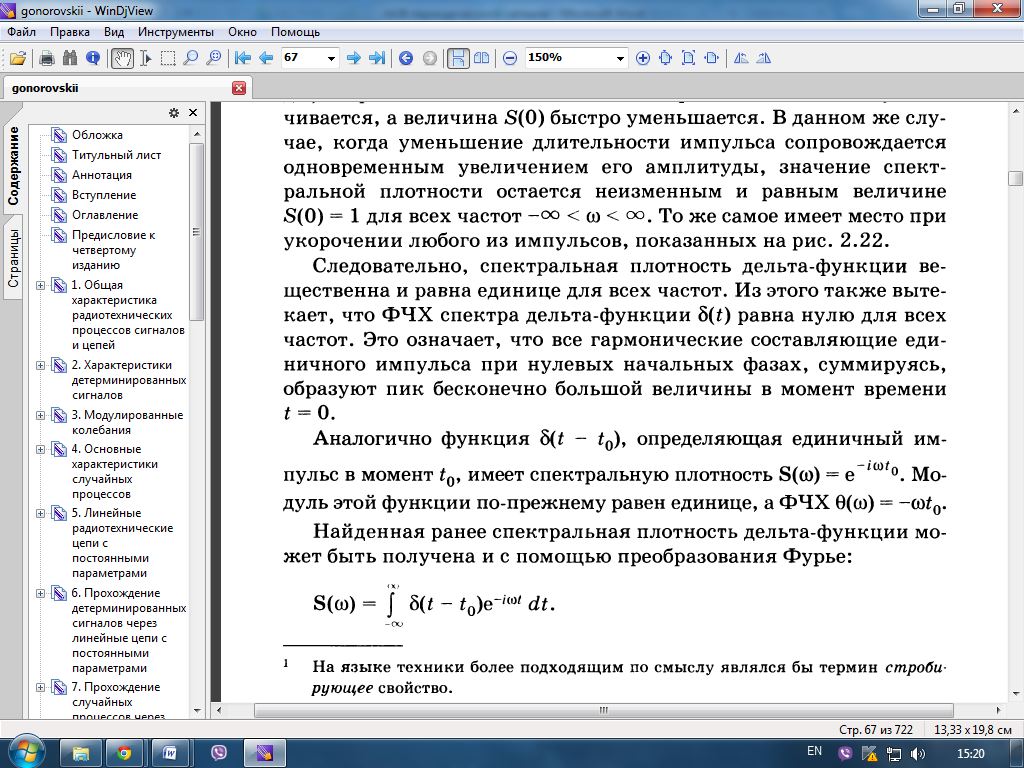
48. Прямое и обратное преобразование Лапласа


![]()
(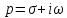 –комплексная частота; позволяет
устранить ограничения, вытекающие из
абсолютной интегрируемости сигнала)
–комплексная частота; позволяет
устранить ограничения, вытекающие из
абсолютной интегрируемости сигнала)
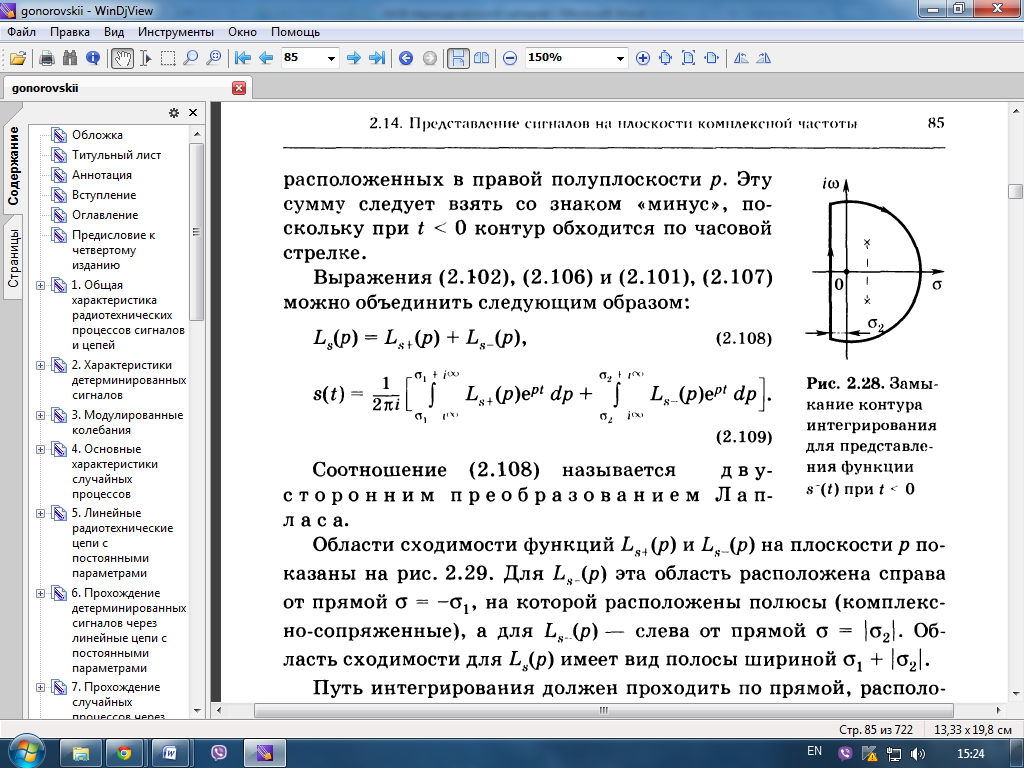
(По логике (2.109) наз. обратное (двустороннее) преобразование Лапласа)
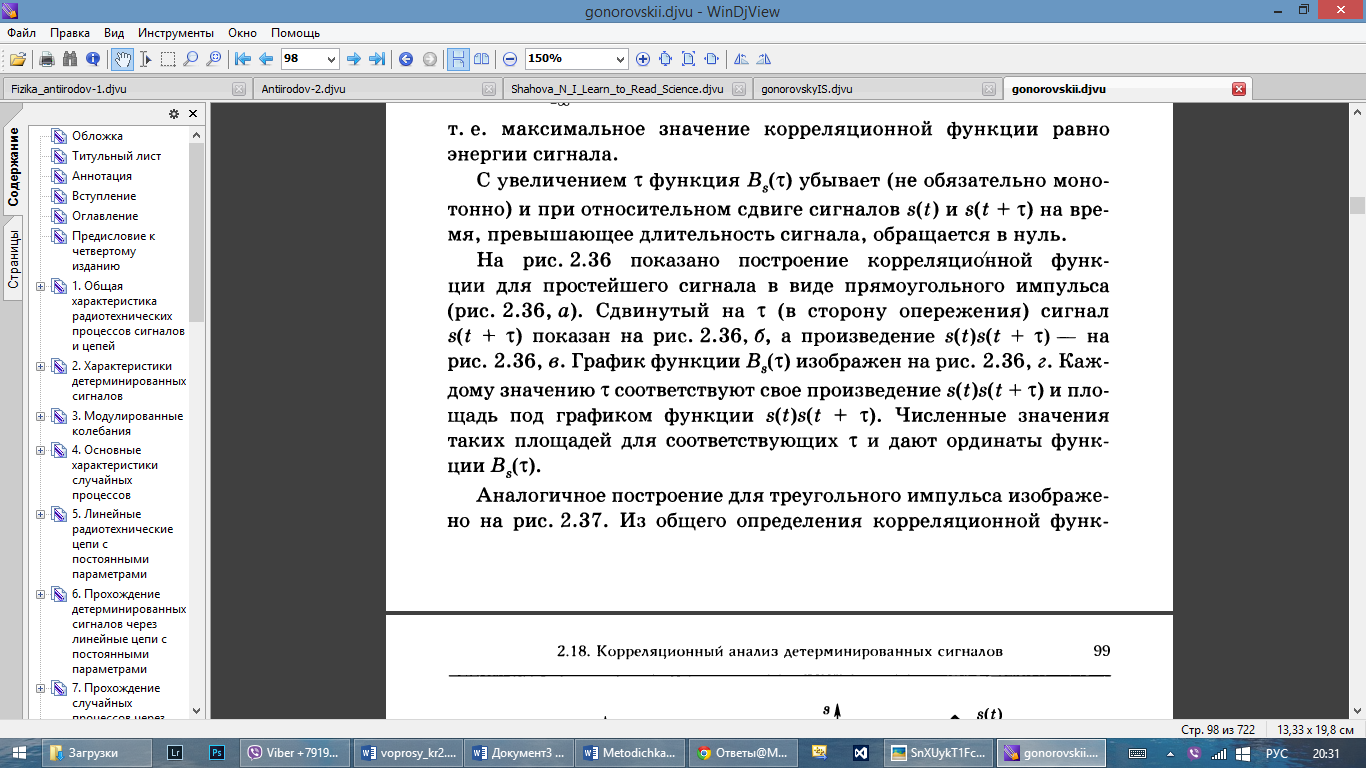
49. АКФ прямоугольного импульса

50. Определение число степеней свободы
Для
сигнала длительностью
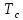 с полосой частот
с полосой частот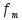 общее
число независимых параметром [т.e.Значений
общее
число независимых параметром [т.e.Значений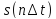 ],
которое необходимо для полного задания
сигнала, будет
],
которое необходимо для полного задания
сигнала, будет![]() При этом
При этом![]()
Число
Nназывают числом степеней
свободы(или базой) сигнала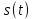 ,
так как даже при произвольном выборе
значений
,
так как даже при произвольном выборе
значений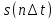 ]
предыдущая сумма определяет функцию,
удовлетворяющую условиям заданного
спектра и заданной длительности сигнала.
]
предыдущая сумма определяет функцию,
удовлетворяющую условиям заданного
спектра и заданной длительности сигнала.
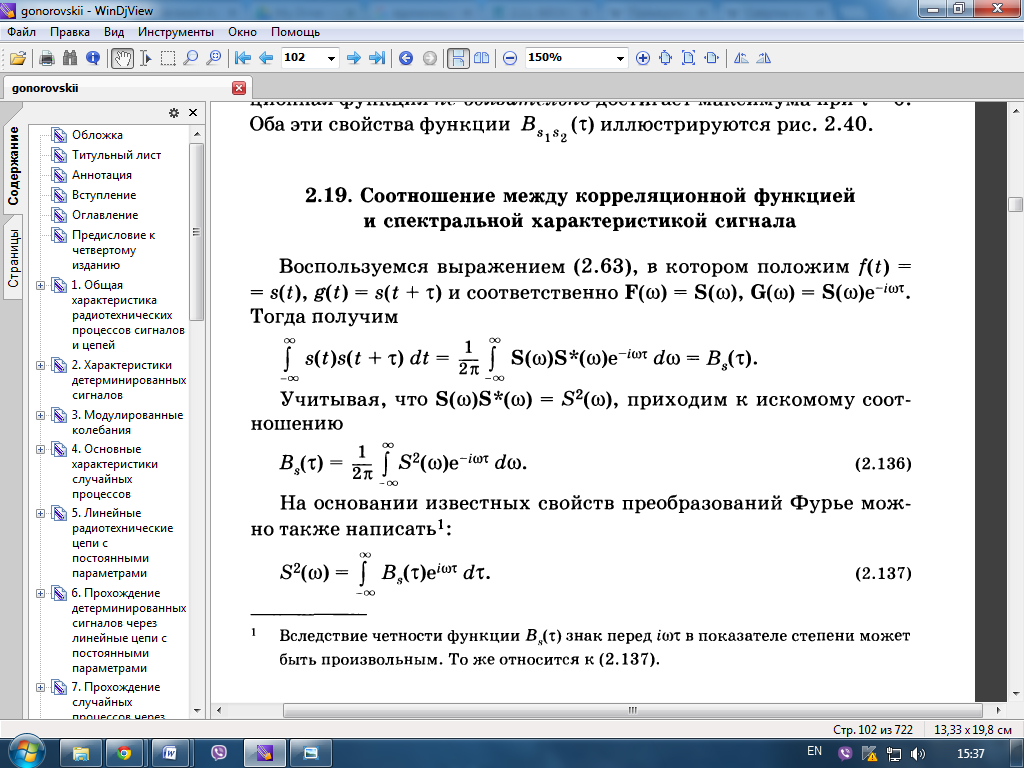
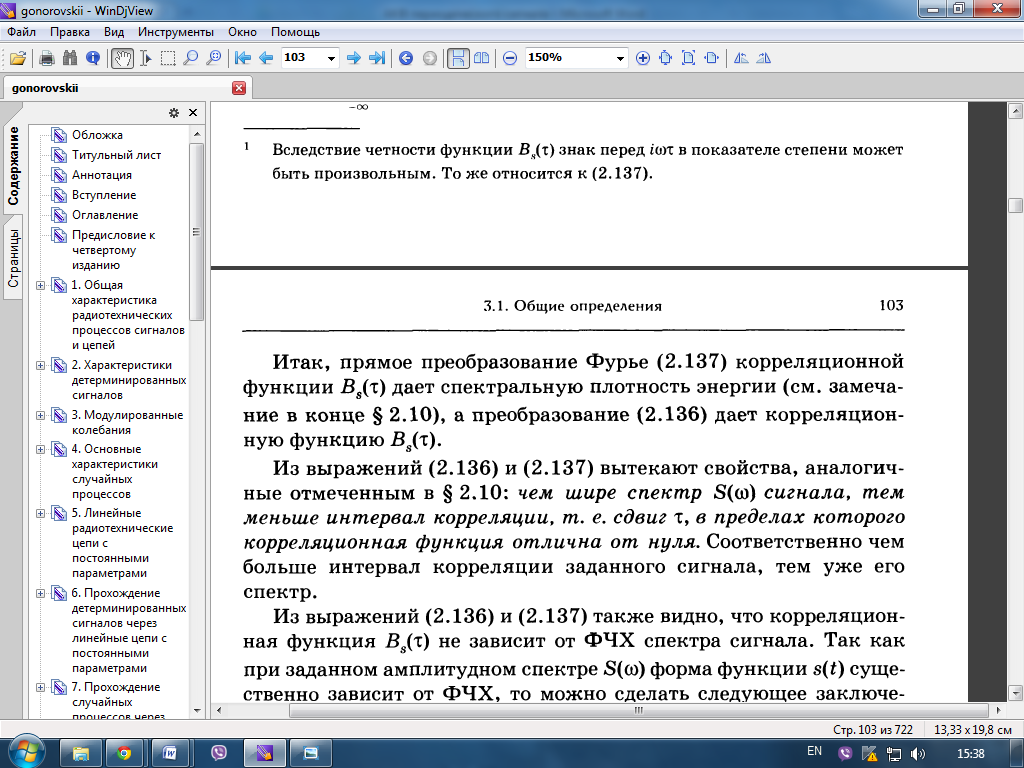
51. Соответствие между интервалом корреляции и шириной спектральной плотности
52.
Зависимость АЧХ от ФЧХ
53. Средняя мощность при разложении в ряд Котельникова

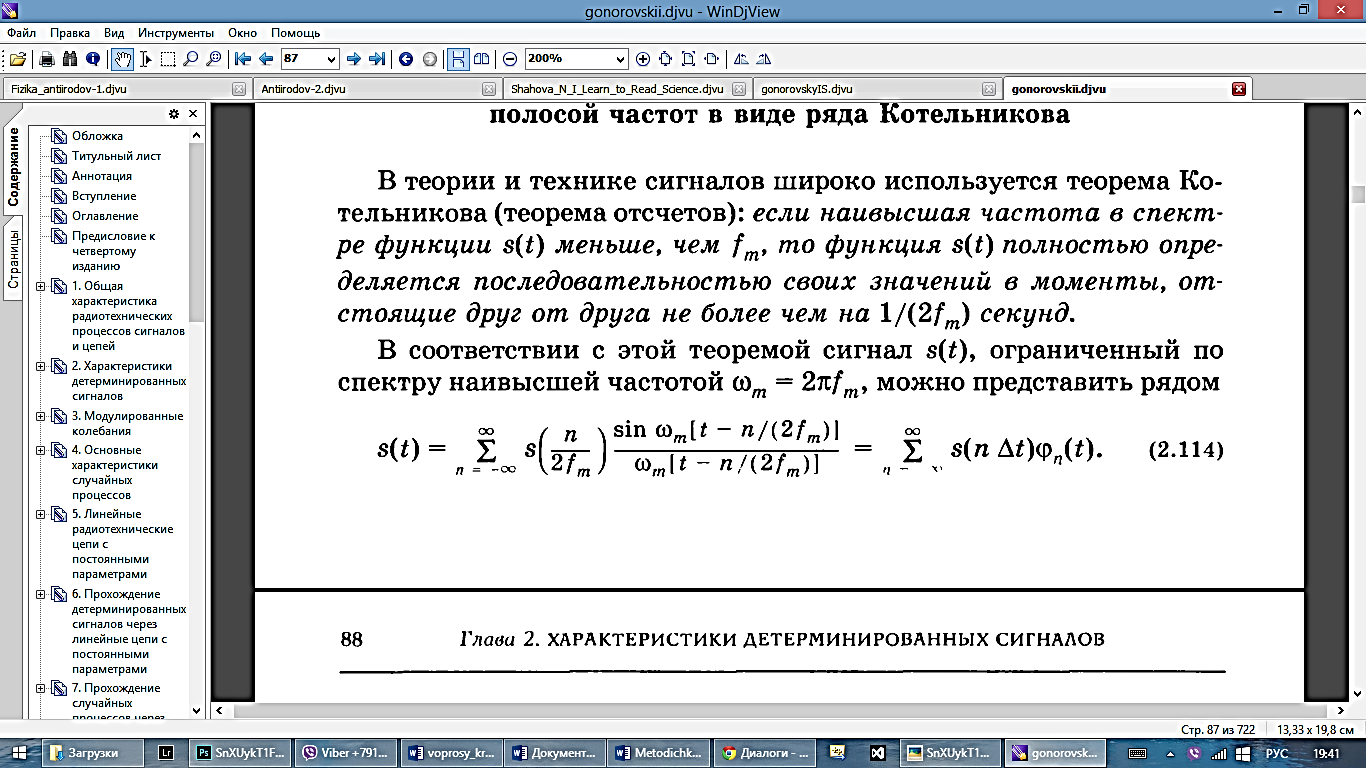
54. Теорема отсчетов
Теорема:если
наивысшая частота в спектре ф-ии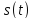 меньше,
чем
меньше,
чем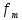 , то ф-ия
, то ф-ия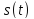 полностью определяется последовательностью
своих значений в моменты, отстоящие
друг от друга не более чем на
полностью определяется последовательностью
своих значений в моменты, отстоящие
друг от друга не более чем на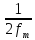 секунд.
секунд.
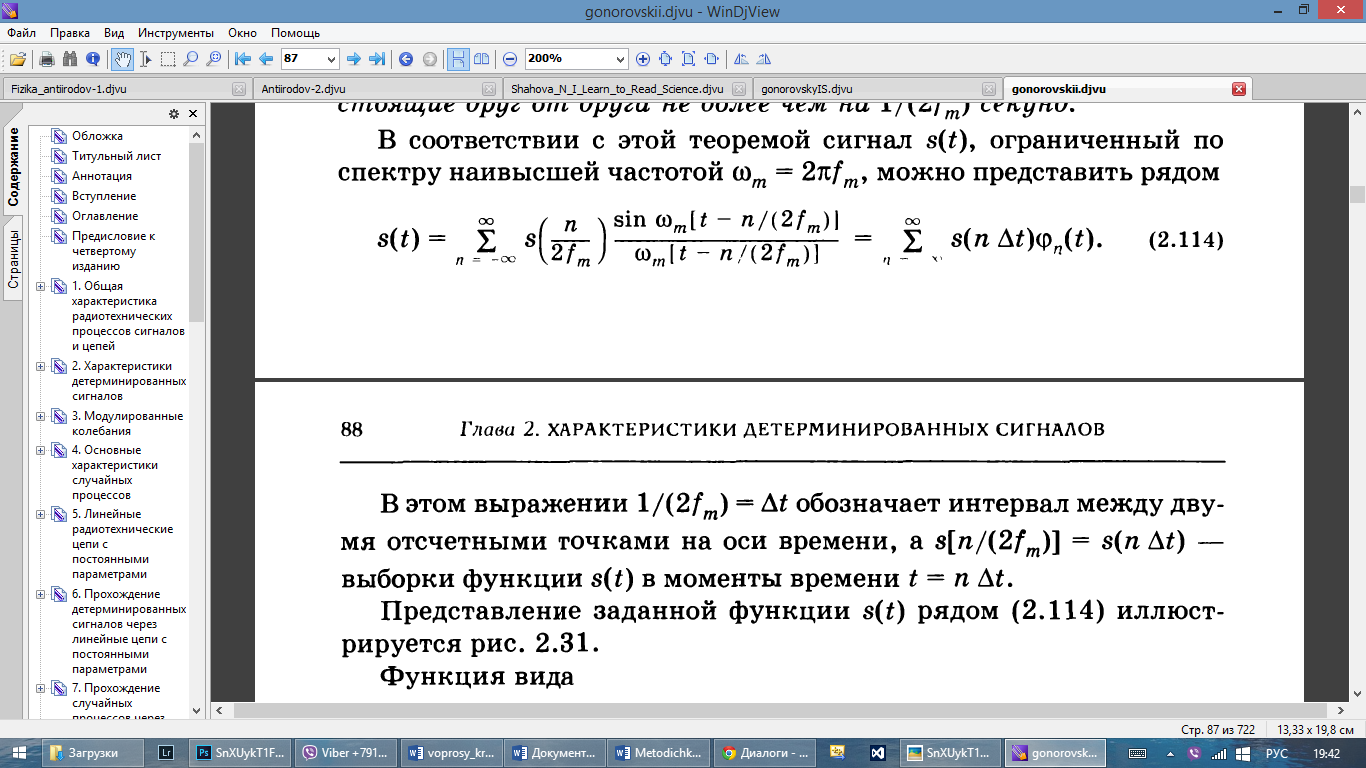
54. Теорема отсчетов в частотной области
Теорема:если
наивысшая частота в спектре ф-ии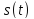 меньше,
чем
меньше,
чем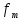 , то ф-ия
, то ф-ия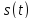 полностью определяется последовательностью
своих значений в моменты, отстоящие
друг от друга не более чем на
полностью определяется последовательностью
своих значений в моменты, отстоящие
друг от друга не более чем на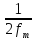 секунд.
секунд.

55. Набор шага дискретизации. ????????????? (Взято аналогично с вопроса №39)
Промежуток времени между соседними моментами взятия выборок (дискретизации) называется шагом дискретизации
![]()

56. Спектр треугольного импульса
Импульс:
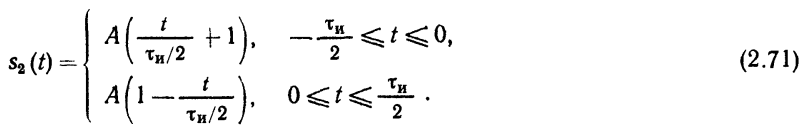
Спектральная плотность импульса:
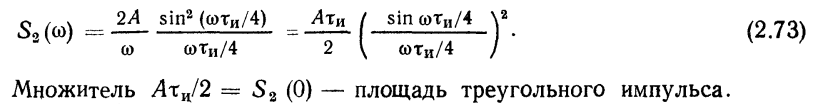
График импульса и спектральной плоскости:
57.
Вид дискретной функции
![]()
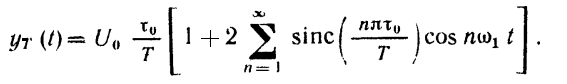
Где
![]() - длительность прямоугольного импульса
- длительность прямоугольного импульса
58. Представление во временной и спектральной плоскости дискретизованного сигнала
График
дискретизованного сигнала, как результат
умножения![]() :
:
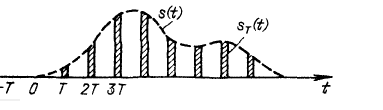
Спектр дискретизованного сигнала и его формула:
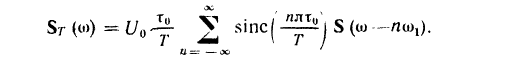
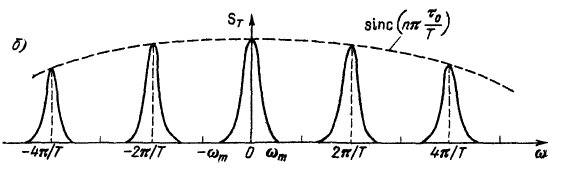
59. (???) Дельта-функция и её свойства

Фильтрующее свойство дельты функции:
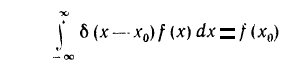
От t:
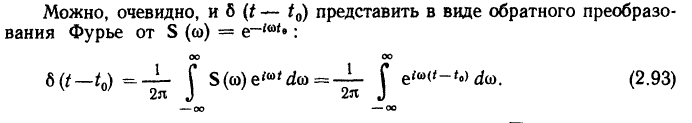
*Энергия единичного импульса бесконечно велика
От
омеги:

60. Изображение по Лапласу дискретизованного сигнала
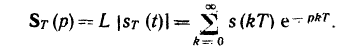
61. Ряд Котельникова
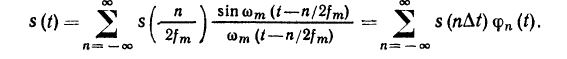
Где
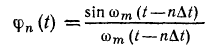
62. Связь между энергетическим спектром сигнала и его корреляционной функцией

