
Каким образом изменится спектр периодического сигнала, если период его повторения устремить в бесконечность?
В этом случае число гармонических составляющих, образующих ряд Фурье, будет бесконечно большим, расстояние между спектральными линиями становится бесконечно малым, а спектр сигнала – сплошным.
Какая связь существует между сплошным спектром непериодического сигнала и линейчатым спектром соответствующего периодического сигнала?
Выражение спектральной плотности сигнала S() отличается от выражения для коэффициентов Сnкомплексного ряда Фурье периодического сигнала только отсутствием множителя 1/T,
Запишите и прокомментируйте выражение для спектральной плотности непериодического сигнала.
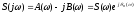
,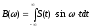
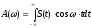
где
Соответственно
модуль спектральной плотности
характеризует амплитудно-частотную
характеристику (АЧХ) сплошного спектра
непериодического сигнала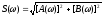
а
аргумент спектральной плотности
характеризует фазочастотную
характеристику (ФЧХ) сплошного спектра
непериодического сигнала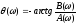
Как связаны между собой длительность импульса и ширина его спектра?
Изменение
масштаба времени, т.е. сжатие или
расширение сигнала во времени в nраз, когда , приводит, соответственно,
к расширению или сжатию во столько же
раз модуля его спектральной плотности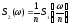
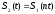
Каков спектр единичного скачка?
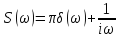
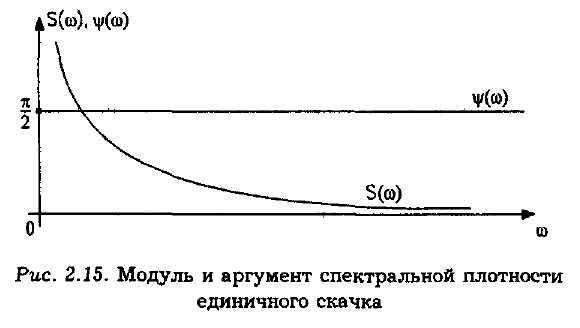
Каков спектр единичного импульса?
прямоугольный импульс
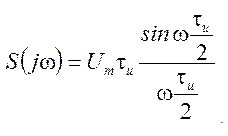 Um-амплитуда
Um-амплитуда
(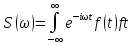 – для любого импульса ,заданного функциейf(t))
– для любого импульса ,заданного функциейf(t))
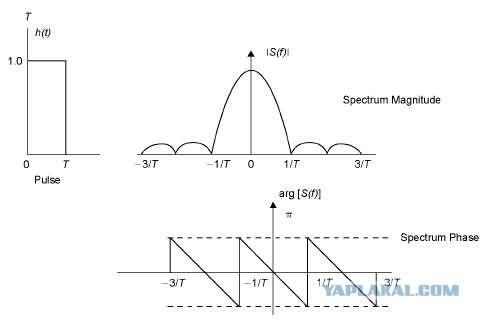
Каков спектр радиоимпульса?(2 варианта ответа)
1.
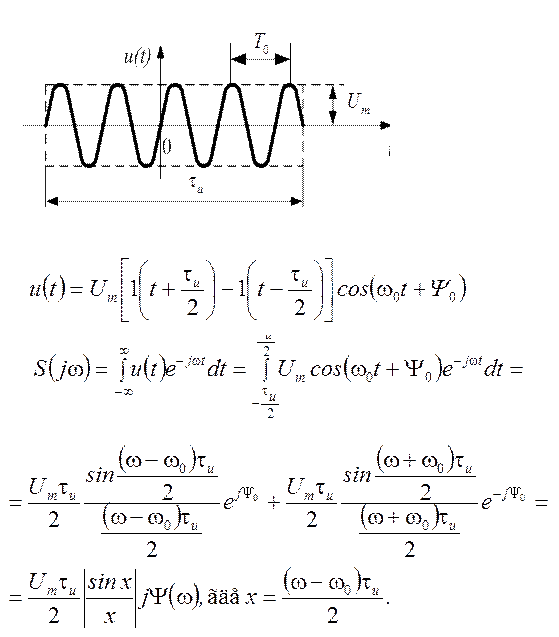
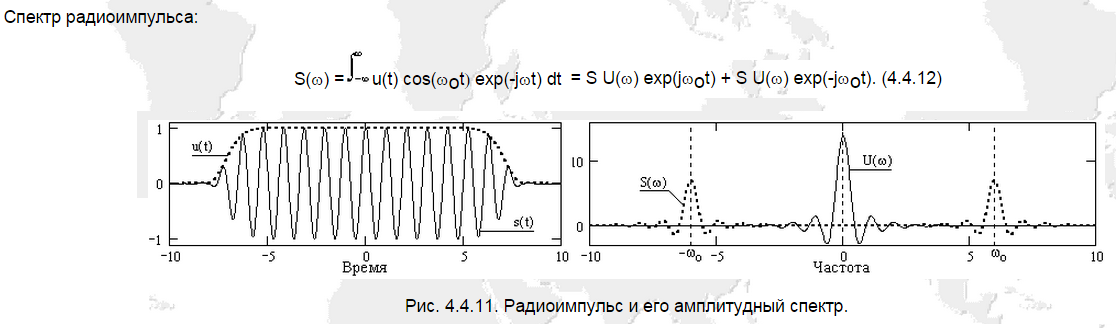
2.
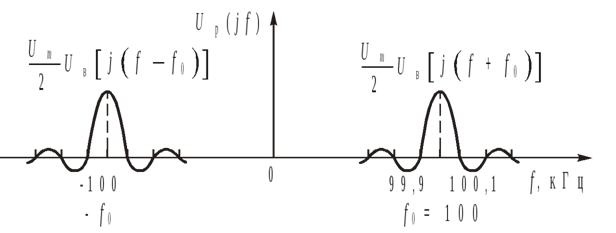
Как определить полосу частот, в которой заключена заданная часть энергии сигнала?
через равенство Парсеваля
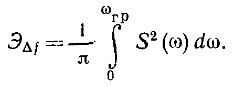
9. Сравнить спектры периодической последовательности видеоимпульсов и пачки из нескольких этих же им
В чем заключается сущность теоремы Котельникова?
Если
наивысшая частота в спектре функции
s(t)
меньше, чем fm,
то функция s(t)
полностью определяется последовательностью
своих значений в моменты, отстоящие
друг от друга не более чем на t=1/(2fm)
секунд.В соответствии с этой теоремой
сигнал s(t),
ограниченный по спектру наивысшей
частотой
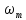 =2
=2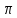 fm,
можно представить рядом
fm,
можно представить рядом
s(t)=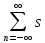 (n/2fm)((sin
(n/2fm)((sin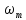 [t-n/(2fm)])/(
[t-n/(2fm)])/(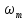 [t-n/(2fm)]))=
[t-n/(2fm)]))=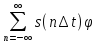 n(t)
n(t)
В чем заключается сущность теоремы отсчетов в частотной области?
Спектральную
плотность s(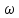 )
необходимо представить рядом, аналогичнымs(t)=
)
необходимо представить рядом, аналогичнымs(t)=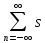 (n/2fm)((sin
(n/2fm)((sin [t-n/(2fm)])/(
[t-n/(2fm)])/(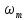 [t-n/(2fm)]))=
[t-n/(2fm)]))=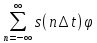 n(t)
для этого базисная функция
n(t)
для этого базисная функция
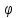 n(t)=(sin
n(t)=(sin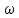 n(t-n
n(t-n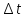 )/
)/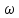 n(t-n
n(t-n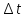 ))sin
c[
))sin
c[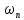 (t-n
(t-n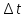 )]
должна быть заменена на
)]
должна быть заменена на
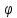 n(
n(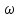 )=sin
c[
)=sin
c[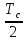 (
(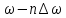 )]
Она получается путем заменыt
на
)]
Она получается путем заменыt
на
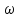 ,
а
,
а
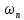 на
на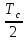
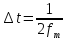

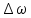 =
=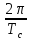
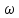 =
=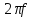 =
=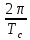 s(
s(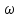 )=
)=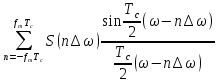
12. Спектр непериодических сигналов.
Спектр
непериодического сигнала непрерывен,
он содержит все частоты. Функция
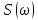 представляет собой спектральную
плотность комплексной амплитуды. Формула
для ее вычисления
представляет собой спектральную
плотность комплексной амплитуды. Формула
для ее вычисления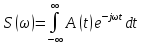 .
.
Спектр непериодического сигнала в отличие от спектра периодического сигнала является сплошным и представляет собой сумму бесконечного числа гармонических составляющих с бесконечно малыми амплитудами.
Обратное преобразование Фурье.
s(t)=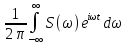 обратное преобразование Фурье
обратное преобразование Фурье
Энергия непериодического сигнала
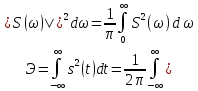
Это важное соотношение, устанавливающее связь между энергией сигнала и модулем его спектральной плотности, известно под названием равенство Парсеваля. Важно отметить, что энергия непериодического сигнала не зависит от фазировки спектральных составляющих. Это является, как и для периодического сигнала, результатом ортогональности спектральных составляющих. Различие заключается в интервалах ортогональности: период Т для периодического сигнала и бесконечно большой интервал для непериодического сигнала.
Из
выражения видно, что величину
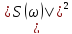 ,
имеющую смысл энергии, приходящейся на
1 Гц, можно рассматривать как спектральную
плотность энергии сигнала.
,
имеющую смысл энергии, приходящейся на
1 Гц, можно рассматривать как спектральную
плотность энергии сигнала.
Выражение корреляционной функции непериодического детерминированного сигнала.
Корреляционная функция сигнала это временная характеристика, которая давала бы представление о некоторых свойствах сигнала, в частности о скорости изменения во времени, а также о длительности сигнала без разложения его на гармонические составляющие.Для детерминированного сигнала s(t) конечной длительности корреляционная функция определяется следующим выражением:
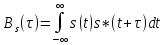 ,
где -временной сдвиг сигнала.
,
где -временной сдвиг сигнала.
Обозначение
комплексного сопряжения можно опустить: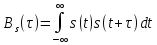
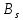 (
(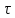 )
характеризует степень связи (корреляции)
сигналаs(t)
со своей копией, сдвинутой на величину
)
характеризует степень связи (корреляции)
сигналаs(t)
со своей копией, сдвинутой на величину
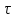 по оси времени. Ясно, что функция
по оси времени. Ясно, что функция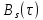 достигает максимума при
достигает максимума при
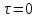 ,
так как любой сигнал полностью коррелирован
с самим собой. При этом
,
так как любой сигнал полностью коррелирован
с самим собой. При этом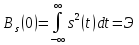 ,
т.е макс-ое значение корр-ой функции
равно энергии сигнала.
,
т.е макс-ое значение корр-ой функции
равно энергии сигнала.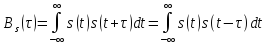 . Это равносильно утверждению, что
. Это равносильно утверждению, что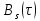 является четной функцией
является четной функцией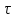 .
.
Выражение свертки
Произведению
двух спектров F(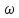 )
)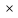 G(
G(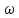 )=S(
)=S(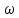 )
соответствует функция времениs(t),
являющаяся сверткой функций f(t)
и g(t):
s(t)=
)
соответствует функция времениs(t),
являющаяся сверткой функций f(t)
и g(t):
s(t)=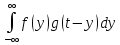 =
=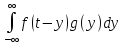 =
=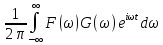
Выражение спектра произведения двух функций.
Пусть рассматриваемый сигнал s(t) является произведением двух функций времени f(t) и g(t).
Спектр сигнала s(t)
S(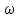 )=
)=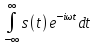 =
=
Каждую функцию f(t) и g(t) можно представить в виде интеграла Фурье:
f(t)=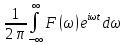 , g(t)=
, g(t)=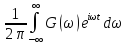
спектр
произведения двух функций f(t)
и g(t)
равен (с кф-ом
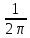 )
свертке их спектровF(
)
свертке их спектровF(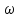 )
иG(
)
иG(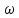 ).
).
В
частном случае
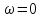 вытекает следующее равенство
вытекает следующее равенство
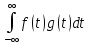 =
=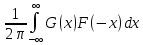
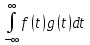 =
=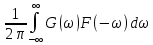 =
=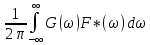 .
.
Спектр суммы сигналов.

