
- •Функция многих переменных: определение, геометрический смысл, область определения, область значений, линия уровня, поверхность уровня.
- •Частные приращения функции двух аргументов, частные производные первого порядка, частные производные высших порядков
- •Сложные функции и их дифференцирование.
- •Неявные функции и их дифференцирование.
- •Экстремум функции двух переменных, условный экстремум, наибольшее и наименьшее значение функции в замкнутой области.
- •Полное приращение и полный дифференциал функции двух аргументов первого порядка. Применение полного дифференциала к приближенным вычислениям.
- •Дифференциалы высших порядков от функции двух аргументов.
- •Касательная плоскость и нормаль к поверхности в заданной точке.
- •Скалярное поле, производная по направлению, градиент, их свойства.
- •Первообразная. Неопределенный интеграл: его свойства, геометрический смысл.
- •Интегрирование тригонометрических функций
- •Интегрирование дробно-рациональных функций.
- •Интегрирование некоторых трансцендентных функций.
- •Интегрирование простейших иррациональных алгебраических функций.
- •Интегрирование гиперболических функций
- •Интегральная сумма, определенный интеграл (определение, теорема существования, основные свойства, правила вычисления)
- •Геометрические приложения определенного интеграла: вычисление площади плоской фигуры, длины дуги плоской кривой, объема тела.
- •Физические приложения определенного интеграла: статические моменты и моменты инерции плоских дуг и фигур, нахождение координат центра тяжести, теоремы Гульдена, вычисление работы и давления
- •Несобственные интегралы: определение, признаки сравнения
- •Двойной интеграл: определение, геометрический смысл, свойства, правила вычисления, замена переменных
- •Геометрические приложения двойного интеграла: площадь плоской фигуры, объем тела, площадь поверхности
- •Физические приложения двойного интеграла: масса, статические моменты, координаты центра тяжести и моменты инерции пластины.
- •Тройной интеграл: определение, геометрический смысл, теорема существования, свойства, вычисление, теорема о среднем значении.
- •Приложения тройного интеграла: объем тела, масса, координаты центра тяжести, геометрические моменты инерции.
-
Физические приложения двойного интеграла: масса, статические моменты, координаты центра тяжести и моменты инерции пластины.
Масса и статические моменты пластины
Предположим,
что плоская пластина изготовлена из
неоднородного материала и занимает
область R в
плоскости Oxy.
Пусть плотность пластины в точке (x,
y) в
области R равна ![]() .
Тогда масса
пластинывыражается
через двойной интеграл в виде
.
Тогда масса
пластинывыражается
через двойной интеграл в виде
![]()
Статический момент пластины относительно оси Ox определяется формулой
![]()
Аналогично находится статический момент пластины относительно оси Oy :
![]()
Координаты центра
масс пластины,
занимающей область R в
плоскости Oxy с
плотностью, распределенной по закону ![]() ,
описываются формулами
,
описываются формулами

Для
однородной пластины с плотностью ![]() для
всех (x,
y) в
области R центр
масс определяется только формой области
и называется центроидом.
для
всех (x,
y) в
области R центр
масс определяется только формой области
и называется центроидом.
Моменты инерции пластины
Момент инерции пластины относительно оси Ox выражается формулой
![]()
Аналогично вычисляется момент инерции пластины относительно оси Oy :
![]()
Полярный момент инерции пластины равен
![]()
Заряд пластины
Предположим,
что электрический заряд распределен
по области R в
плоскости Oxy и
его плотность распределения задана
функцией ![]() .
Тогда полный заряд
пластины Q определяется
выражением
.
Тогда полный заряд
пластины Q определяется
выражением
![]()
-
Тройной интеграл: определение, геометрический смысл, теорема существования, свойства, вычисление, теорема о среднем значении.
Тройной интеграл от функции U=f(x,y,z), распространенным на область V, называется предел соответствующей трехкратной суммы.

Геометрический смысл двойного интеграла.
Рассмотрим тело V, ограниченное частью поверхности, задаваемой уравнением z = f(x, y), проекцией D этой поверхности на плоскость Оху и боковой цилиндрической поверхностью, полученной из вертикальных образующих, соединяющих точки границы поверхности с их проекциями.
Будем
искать объем этого тела как предел суммы
объемов цилиндров, основаниями которых
являются части ΔSi области D, а высотами
– отрезки длиной f(Pi), где точки Pi
принадлежат ΔSi. Переходя к пределу
при ![]() ,
получим, что
,
получим, что
![]() (7.12)
(7.12)
то есть двойной интеграл представляет собой объем так называемого цилиндроида, ограниченного сверху поверхностью z = f(x, y), а снизу – областью D.
Теорема существования тройного интеграла. Если подынтегральная функция непрерывна на области V, то она интегрируема по этой области.
Вычисление тройного интеграла сводится к последовательному вычислению обыкновенных (однократных) интегралов.
Пусть функции f (x,y,z) и g (x,y,z) интегрируемы в области U. Тогда справедливы следующие свойства:
-
 ,
где k -
константа;
,
где k -
константа;
-
Если
 в
любой точке области U,
то
в
любой точке области U,
то 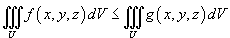 ;
;
-
Если область U является объединением двух непересекающихся областей U1 и U2, то
 ;
;
-
Пусть m - наименьшее и M - наибольшее значение непрерывной функции f (x,y,z) в области U. Тогда для тройного интеграла справедлива оценка:
![]()
где V - объем области интегрирования U.
-
Теорема о среднем значении тройного интеграла. Если функция f (x,y,z) непрерывна в области U, то существует точка M0
 U,
такая, что
U,
такая, что
![]()
где V - объем области U.
