
- •Функция многих переменных: определение, геометрический смысл, область определения, область значений, линия уровня, поверхность уровня.
- •Частные приращения функции двух аргументов, частные производные первого порядка, частные производные высших порядков
- •Сложные функции и их дифференцирование.
- •Неявные функции и их дифференцирование.
- •Экстремум функции двух переменных, условный экстремум, наибольшее и наименьшее значение функции в замкнутой области.
- •Полное приращение и полный дифференциал функции двух аргументов первого порядка. Применение полного дифференциала к приближенным вычислениям.
- •Дифференциалы высших порядков от функции двух аргументов.
- •Касательная плоскость и нормаль к поверхности в заданной точке.
- •Скалярное поле, производная по направлению, градиент, их свойства.
- •Первообразная. Неопределенный интеграл: его свойства, геометрический смысл.
- •Интегрирование тригонометрических функций
- •Интегрирование дробно-рациональных функций.
- •Интегрирование некоторых трансцендентных функций.
- •Интегрирование простейших иррациональных алгебраических функций.
- •Интегрирование гиперболических функций
- •Интегральная сумма, определенный интеграл (определение, теорема существования, основные свойства, правила вычисления)
- •Геометрические приложения определенного интеграла: вычисление площади плоской фигуры, длины дуги плоской кривой, объема тела.
- •Физические приложения определенного интеграла: статические моменты и моменты инерции плоских дуг и фигур, нахождение координат центра тяжести, теоремы Гульдена, вычисление работы и давления
- •Несобственные интегралы: определение, признаки сравнения
- •Двойной интеграл: определение, геометрический смысл, свойства, правила вычисления, замена переменных
- •Геометрические приложения двойного интеграла: площадь плоской фигуры, объем тела, площадь поверхности
- •Физические приложения двойного интеграла: масса, статические моменты, координаты центра тяжести и моменты инерции пластины.
- •Тройной интеграл: определение, геометрический смысл, теорема существования, свойства, вычисление, теорема о среднем значении.
- •Приложения тройного интеграла: объем тела, масса, координаты центра тяжести, геометрические моменты инерции.
-
Касательная плоскость и нормаль к поверхности в заданной точке.
Касательная плоскость к поверхности в её точке M0(точка касания) есть плоскость, проходящая через M0 и содержащая в себе все касательные, проведённые в точке M0 ко всевозможным кривым, проведённым на поверхности через точку M0.
Нормалью к поверхности в точке M0 называется прямая, проходящая через точку M0 и перпендикулярная к касательной плоскости, проведённой в этой точке.
Если уравнение поверхности имеет вид F(x, y, z)=0, то уравнение касательной плоскости в точке M0(x0,y0,z0), имеет вид:
![]()
Уравнение нормали к этой поверхности в точке M0 есть

В случае явного задания поверхности уравнением примут вид

-
Скалярное поле, производная по направлению, градиент, их свойства.
Скалярным полем называется часть пространства (или все пространство), каждой точке M которой соответствует численное значение некоторой скалярной величины u. Скалярная величина u не зависит от времени, а зависит только от положения точки M в пространстве, это значит, рассматривается как функция точки M : u = f(M ) . Эта функция называется функцией поля. Если в пространстве выбрана система координат Oxyz, то скалярная величина u является функцией координат x, y , z, т.е. u = f(M)= f(x, y,z)
Наоборот, каждая функция трех переменных u = f(x, y,z) задает некоторое скалярное поле.
Геометрическим изображением скалярного поля являются поверхности уровня.
Пусть
в некоторой области D задана
функция u=u(x,y,z) и
точка M(x,y,z) .
Проведем из точки M вектор ![]() ,
направляющие косинусы которого cos
α, cos
β, cos
γ .
На векторе
,
направляющие косинусы которого cos
α, cos
β, cos
γ .
На векторе ![]() ,
на расстоянии
,
на расстоянии ![]() от
его начала рассмотрим точку
от
его начала рассмотрим точку ![]() ,
т.е.
,
т.е. ![]() .
.

 .
Пусть
в каждой точке некоторой области D задана
функция u=u(x,y,z) .
Вектор,
проекциями которого на оси координат
являются значения частных производных
этой функции в соответствующей точке,
называется градиентом
функции u=u(x,y,z) и
обозначается grad
u или ⍢u :
.
Пусть
в каждой точке некоторой области D задана
функция u=u(x,y,z) .
Вектор,
проекциями которого на оси координат
являются значения частных производных
этой функции в соответствующей точке,
называется градиентом
функции u=u(x,y,z) и
обозначается grad
u или ⍢u : 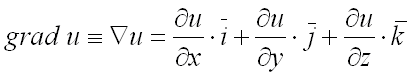 .
.
При этом говорят, что в области D определено векторное поле градиентов.
Для
нахождения градиента функции u=u(x,y,z) в
заданной точке M0(x0,y0,z0) используют
формулу:
 .
.

-
Первообразная. Неопределенный интеграл: его свойства, геометрический смысл.
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство F’(x)=f(x) для любого х из заданного промежутка.
Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство (F(x)+C)’=f(x) . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
Все
множество первообразных функции f(x) называется
неопределенным
интегралом
этой функции и обозначается ![]() .
.
Выражение f(x)dx называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
-
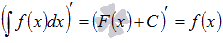 Производная
результата интегрирования равна
подынтегральной функции.
Производная
результата интегрирования равна
подынтегральной функции. -
 Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы. -
 ,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла. -
 Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для
доказательства третьего и четвертого
свойств достаточно найти производные
от правых частей равенств:

Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых линий y=F(x)+C. График каждой первообразной называется интегральной кривой.
-
Таблица основных интегралов.

-
Основные методы интегрирования: подведение функции под знак дифференциала, интегрирование методом разложения, интегрирование методом замены переменной (непосредственное, подстановкой), интегрирование по частям.
Метод
подведения под знак дифференциала
основан
на равенстве
![]() .
.
То есть, главной задачей является приведение подынтегральной функции к виду f(g(x))d(g(x)).
Пусть
требуется найти неопределенный
интеграл ∫f(x)dx
. Предположим, что существуют
дифференцируемые функции ![]() и
и ![]() такие,
что
такие,
что
![]()
Тогда
![]()
Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала.
Тогда,
если ∫f(x)dx=F(x)+c и ![]() ,
то имеет место следующее равенство:
∫f(u)du=F(u)+C
,
то имеет место следующее равенство:
∫f(u)du=F(u)+C
Рассмотрим функции u=u(x) и v=v(x), которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство: d(uv)=udv+vdu
Проинтегрировав левую и правую части последнего равенства, получим:
![]()
Полученное равенство перепишем в виде: ∫udv=uv-∫vdu
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл ∫udv можно свести к нахождению интеграла ∫vdu , который может быть более простым.
Замена переменной.
Пусть
требуется найти неопределенный интеграл
 .
Сделаем замену в подынтегральном
выражении, положив x=φ(t),
где φ(t) —
монотонная непрерывная функция, которая
имеет непрерывную производную. Тогда dx=
φ’(t)dt.
В этом случае имеет следующее равенство:
.
Сделаем замену в подынтегральном
выражении, положив x=φ(t),
где φ(t) —
монотонная непрерывная функция, которая
имеет непрерывную производную. Тогда dx=
φ’(t)dt.
В этом случае имеет следующее равенство:

