Численность населения на одного врача в Кемеровской области

2000	2001	2002	2003	2004	2005
221,6	219,9	217,8	215,8	212,6	212,8
2006	2007	2008	2009	2010	2011
209,5	207	207,7	207,4	209,5	206,8

Необходимо проверить наличие тенденции в данном ряде динамики методом сравнения средних уровней ряда динамики.

Решение.Разобьем исходный ряд динамики на 2 равные части:

– в первую войдут значения показателя с 2000 по 2005 гг.,

– во вторую — с 2006 по 2011 гг.

Рассчитаем выборочные характеристики:

.

Если в ряду динамики существует тенденция средней, то средние, вычисленные для двух совокупностей, должны значимо различаться между собой.

Выдвигаем гипотезу , проверяем ее на основе t-критерия Стьюдента:

.

.

, следовательно гипотеза о равенстве средних двух совокупностей отвергается с вероятностью ошибки 0,05, средние существенно различаются между собой, в ряду динамики численности населения на одного врача Кемеровской области существует тенденция средней и, следовательно, в ряду динамики существует тренд.

Проверим гипотезу H0 о равенстве дисперсий двух нормально распределенных совокупностей на основе F-критерия Фишера — Снедекора.

, ,.

Так как Fp > Fкр, то гипотеза H0 о равенстве дисперсий двух нормально распределенных совокупностей отвергается с вероятностью ошибки 0,05, следовательно, расхождение между дисперсиями существенно, в ряду динамики численности населения на одного врача Кемеровской области существует тенденция дисперсий, следовательно, в ряду динамики существует тренд.

Метод Фостера-Стюарта основан на двух простых характеристиках S и d.

,

где: .

Суммирование производится по всем членам ряда. Значения иопределяются путем последовательного сравнения уровней.

Если значение уровня ряда превышает по своей величине каждый из предыдущих уровней, то величине присваивается значение 1, в остальных случаях она равна 0. Таким образом:

Наоборот, если значение уровня ряда меньше всех предыдущих, то присваивается значение 1.

Таким образом:

Показатели S и d асимптотически нормальные и имеют независимые распределения, но на них влияет порядок расположения уровней во времени. Показатель S применяется для обнаружения тенденции изменения в дисперсиях, d — для обнаружения тенденций в средней. После того, как для исследуемого ряда найдены фактические значения d и S, проверяется гипотеза о том, можно ли считать случайными разности d — 0 и S — μ.

Гипотезы можно проверять, применяя t-критерий Стьюдента, то есть:

где: μ — математическое ожидание величины S, определенное для случайного расположения уровней во времени;

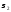, — средние квадратические ошибки величин S и d.

Значения μ, 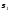,табулированы.

Если , то гипотеза об отсутствии тенденции в средней отвергается, следовательно в исходном временном ряду существует тренд.

Если , то гипотеза об отсутствии тенденции в дисперсиях отвергается, следовательно существует тенденция дисперсии и существует тренд.

Пример 2.3. Проверим наличие тенденции в ряду динамики численности населения на одного врача в Кемеровской области методом Фостера-Стюарта.

Решение.Отразим в таблице 2.3.,,,.

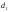Таблица 2.3.