
- •А.С. Березина анализ данных
- •Предисловие
- •Лекция 1. Априорный анализ компонент временного ряда
- •1.1. Понятие временного ряда. Виды временных рядов
- •Производство молока в Кемеровской области
- •Численность работников здравоохранения, перед которыми организация имеет просроченную задолженность по заработной плате работников в Российской Федерации в 2013 году
- •Индекс потребительских цен в Кемеровской области (декабрь к декабрю предыдущего года; в процентах)
- •Потребление сахара (кг) на душу населения в Кемеровской области
- •1.2. Методы оценки однородности исходных данных
- •1.3. Методика выявления и анализа аномальных наблюдений
- •Краткосрочные экономические показатели рф
- •Расчётная таблица примера 1.1.
- •1.4. Абсолютные, относительные и средние показатели в анализе временных рядов
- •ЛЕкция 2. Моделирование тенденции
- •2.1. Проверка гипотезы о существовании тренда
- •Промежуточные расчетные значения кумулятивного т-критерия
- •2.2. Методы выявления тенденции
- •Численность населения на одного врача в Кемеровской области
- •Расчетная таблица метода Фостера-Стюарта
- •2.3. Выбор формы тренда
- •Критерии выбора класса, выравнивающих кривых
- •Лекция 3. Моделирование периодической компоненты
- •3.1. Аддитивные и мультипликативные тренд-сезонные модели Алгоритм построения модели временного ряда, содержащего сезонные колебания:
- •Поквартальные данные по розничному товарообороту компании
- •Расчет коэффициента автокорреляции
- •Коррелограмма временного ряда товарооборота
- •Расчет оценок сезонной компоненты в аддитивной модели
- •Расчет значений сезонной компоненты в аддитивной модели
- •Расчет значений t и ошибок e в аддитивной модели.
- •Расчет оценок сезонной компоненты в мультипликативной модели
- •Расчет значений сезонной компоненты в мультипликативной модели
- •Расчет значений t и ошибок e в мультипликативной модели
- •Лекция 4. Простейшие методы прогнозирования
- •4.1. Метод среднего уровня ряда
- •4.2. Метод среднего абсолютного прироста
- •Расчетная таблица для определения прогнозных значений методом среднего абсолютного прироста
- •4.3. Метод среднего темпа роста
- •4.4. Оценка точности и надежности прогнозов
- •Лекция 5. Методы выбора трендовой модели прогноза
- •5.1. Прогнозирование на основе кривых роста
- •5.2. Прогнозирование на основе экстраполяции тренда
- •Лекция 6. Адаптивные модели прогнозирования
- •6.1. Сущность адаптивных методов
- •6.2. Экспоненциальное сглаживание
- •Индекс потребительских цен Кемеровской области
- •Экспоненциальные средние
- •6.3. Метод гармонических весов
- •Параметры уравнений отдельных фаз движения текущего тренда
- •Лекция 7. Прогнозирование динамических рядов, не имеющих тенденции.
- •Распределение знаков отклонений
- •Расчетная таблица для определения знаков отклонений
- •Распределение знаков отклонений
- •8. Метод экспертных оценок
- •8.1. Методы и модели экспертных оценок
- •Матрица опроса
- •Матрица преобразованных рангов
- •Оценки вкусовых качеств продукта
- •Оценки вкусовых качеств продукта
- •Матрица преобразованных рангов
- •8.2. Методы и модели выбора альтернатив
- •Частные критерии трех операторов
- •Нормализованные критерии
- •Лекция 9. Статистические методы обработки результатов экспертизы
- •9.1. Оценка согласованности мнений экспертов
- •9.2. Обобщение мнений экспертов
- •Список литературы
- •Содержание
- •Анализ данных
- •650992, Г. Кемерово, пр. Кузнецкий, 39
Индекс потребительских цен Кемеровской области
|
t |
|
t |
|
t |
|
t |
|
|
1 |
102,1 |
10 |
100,7 |
19 |
101,3 |
28 |
100,6 |
|
2 |
100,7 |
11 |
100,5 |
20 |
100,6 |
29 |
100,4 |
|
3 |
100,8 |
12 |
100,6 |
21 |
100,8 |
30 |
100,2 |
|
4 |
100,3 |
13 |
100,3 |
22 |
100,7 |
31 |
100,4 |
|
5 |
100,6 |
14 |
100,3 |
23 |
100,6 |
32 |
100,3 |
|
6 |
99,9 |
15 |
100,6 |
24 |
100,5 |
33 |
100,1 |
|
7 |
100,3 |
16 |
100,3 |
25 |
101 |
34 |
101,2 |
|
8 |
99,9 |
17 |
100,4 |
26 |
100,8 | ||
|
9 |
100,1 |
18 |
100,8 |
27 |
100,5 | ||
Решение. Определим
 .
.
Найдем значения экспоненциальной средней при α = 0,1.
 ,
,
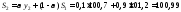
и т.д.
Результаты расчетов представлены в таблице 6.2.
Проведем аналогичные расчеты для α = 0,5.
 ,
,

и т.д.
Результаты расчетов представлены в таблице 6.2.
На рисунке 6.1 наглядно представлено влияние значения параметра адаптации α на характер сглаженного ряда.
При α = 0,1 экспоненциальная средняя носит более гладкий характер, т. к. в этом случае в наибольшей степени поглощаются случайные колебания временного ряда.
Таблица 6.2.
Экспоненциальные средние
|
t |
Экспоненциальная средняя |
t |
Экспоненциальная средняя | ||||
|
|
|
|
| ||||
|
1 |
101,02 |
101,50 |
18 |
100,54 |
100,60 | ||
|
2 |
100,99 |
101,10 |
19 |
100,61 |
100,95 | ||
|
3 |
100,97 |
100,95 |
20 |
100,61 |
100,77 | ||
|
4 |
100,90 |
100,63 |
21 |
100,63 |
100,79 | ||
|
5 |
100,87 |
100,61 |
22 |
100,64 |
100,74 | ||
|
6 |
100,77 |
100,26 |
23 |
100,63 |
100,67 | ||
|
7 |
100,73 |
100,28 |
24 |
100,62 |
100,59 | ||
|
8 |
100,64 |
100,09 |
25 |
100,66 |
100,79 | ||
|
9 |
100,59 |
100,09 |
26 |
100,67 |
100,80 | ||
|
10 |
100,60 |
100,40 |
27 |
100,65 |
100,65 | ||
|
11 |
100,59 |
100,45 |
28 |
100,65 |
100,62 | ||
|
12 |
100,59 |
100,52 |
29 |
100,62 |
100,51 | ||
|
13 |
100,56 |
100,41 |
30 |
100,58 |
100,36 | ||
|
14 |
100,54 |
100,36 |
31 |
100,56 |
100,38 | ||
|
15 |
100,54 |
100,48 |
32 |
100,54 |
100,34 | ||
|
16 |
100,52 |
100,39 |
33 |
100,49 |
100,22 | ||
|
17 |
100,51 |
100,39 |
34 |
100,56 |
100,71 | ||

Рис. 6.1. Экспоненциальное сглаживание временного ряда индекса потребительских цен Кемеровской области
6.3. Метод гармонических весов
Метод гармонических весов, близок к методу простого экспоненциального сглаживания и использует тот же принцип.
В его основе лежит взвешивание скользящего показателя, но вместо скользящей средней используется идея скользящего тренда. Экстраполяция проводится по скользящему тренду, отдельные точки ломаной линии взвешиваются с помощью гармонических весов, что позволяет более поздним наблюдениям придавать большой вес.
Метод гармонических весов базируется на следующих предпосылках:
1. Период времени, за который изучается экономический процесс, должен быть достаточно длительным, чтобы можно было определить его закономерности.
2. Исходный ряд динамики не должен иметь скачкообразных изменений.
3. Прогнозируемое социально-экономическое явление должно обладать инерционностью, то есть для наступления большого изменения в характеристиках процесса необходимо, чтобы прошло значительное время.
4. Отклонения от скользящего тренда (εt) имеют случайный характер.
5. Автокорреляционная функция, рассчитанная на основе последовательных разностей, должна уменьшаться с увеличением уровней временного ряда, то есть влияние более поздней информации должно отражаться на прогнозируемой величине сильнее, чем ранней информации.
Для получения точного прогноза по методу гармонических весов необходимо выполнение всех вышеуказанных предпосылок для исходного ряда динамики.
Для осуществления прогноза данным методом исходный временной ряд разбивается на фазы (к). Число фаз должно быть меньше числа членов ряда (n), то есть к < n. Обычно фаза равна 3-5 уровням. Для каждой фазы рассчитывается линейный тренд, то есть:
 ,
,
при этом: для i = 1, t = 1, 2, 3, … , k; для i= 2,t= 2, 3, … ,k+ 1;
для i = n-k+1 t= n - k + 1, n - k + 2, … , n.
Для
оценки параметров используется способ
наименьших квадратов. С помощью полученных
(n - k + 1) уравнений определяются значения
скользящего тренда
 ,
из которых находится среднее значение
,
из которых находится среднее значение .
.
После этого необходимо проверить гипотезу о том, что отклонения от скользящего тренда представляют собой стационарный процесс. С этой целью рассчитывается автокорреляционная функция. Если значения автокорреляционной функции уменьшаются от периода к периоду, то пятая предпосылка данного метода выполняется.
Далее рассчитываем приросты по формуле:
 .
.
Средняя
приростов вычисляется по формуле:
 ,
,
где:
 - гармонические коэффициенты,
удовлетворяющие следующим условиям:
- гармонические коэффициенты,
удовлетворяющие следующим условиям: ,
, .
.
Данное
выражение позволяет более поздней
информации придавать большие веса, так
как приросты весов обратно пропорциональны
времени, которое отделяет раннюю
информацию от поздней для момента t = n.
Если самая ранняя информация имеет вес
 ,
то вес информации, относящейся к
следующему моменту времени, равен:
,
то вес информации, относящейся к
следующему моменту времени, равен: .
.
В
общем виде ряд гармонических весов
определяют по формуле:
 .
.
Гармонические
коэффициенты
 находятся по формуле :
находятся по формуле : .
.
Далее
прогнозирование сводится, так же как и
при простых методах прогноза, путем
прибавления к последнему значению ряда
динамики среднего прироста, то есть:
 ,
при начальном условии
,
при начальном условии .
.
Пример 6.2. По приведенным данным о плотности автомобильных дорог общего пользования с твердым покрытием в Кемеровской области произвести прогноз на 2012-2013 гг. на основе метода гармонических весов.
Решение. Рассчитаем параметры уравнений отдельных фаз движения текущего тренда методом наименьших квадратов при условии, что интервал сглаживанияk=3 (таблица 6.3).
Таблица 6.3.








