Тема 4. Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)

Закон Ампера. На элемент проводника с током I , помещённый в магнитное поле с индукцией действует сила (–сила Ампера): .

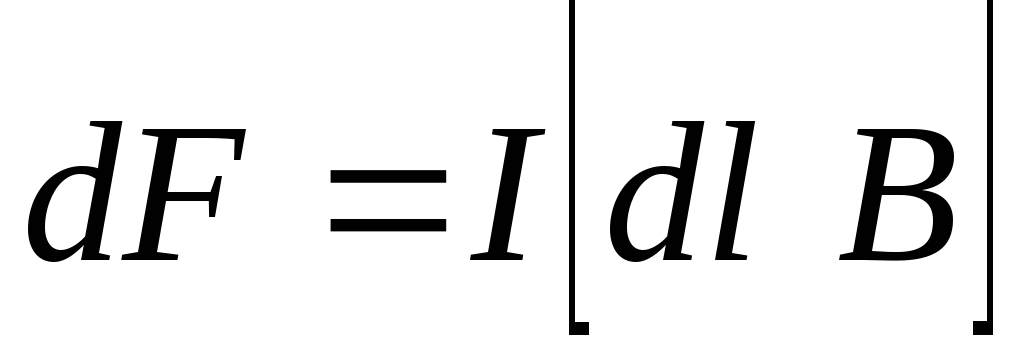Модуль вектора: ,

где – угол между векторами и .

Направление вектора можно определить поправилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление силы Ампера (рис. 13, сила перпендикулярна плоскости рисунка).

Сила Лоренца. На заряд q , движущийся со скоростью в магнитном поле с индукцией , действует сила( –сила Лоренца ): .

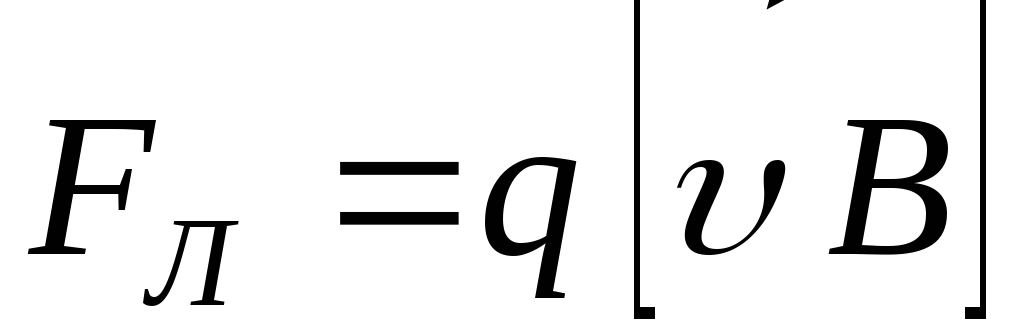Модуль вектора :,

где α – угол между векторами и .

Н

Рис. 14

аправление вектораможет быть определено поправилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов: если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис.14, сила перпендикулярна плоскости рисунка).

Тема. 5. Магнитный поток. Теорема Гаусса для магнитного поля

Поток вектора магнитной индукции (или магнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S. Если площадка S расположена перпендикулярно силовым линиям магнитного поля (рис. 15), то поток Ф_B

вектора индукции через данную площадкуS : .

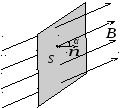
Рис. 15 Рис. 16

Если площадка S расположена неперпендикулярно силовым линиям магнитного поля (рис. 16), то поток Ф_B вектора индукции через данную площадкуS :

,

где α – угол между векторами и нормалик площадкеS.

Д

Рис. 17

ля того, чтобы найти потокФ_B вектора магнитной индукции через произвольную поверхностьS, необходимо разбить эту поверхность на элементарные площадки dS (рис. 17) и определить элементарный поток векторачерез каждую площадкуdS по формуле: ,

где α – угол между векторами и нормалик данной площадкеdS;

–вектор, равный по величине площади площадки dS и направленный по вектору нормали к данной площадке dS .

Тогда поток вектора через произвольную поверхностьS равен алгебраической сумме элементарных потоков через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:

.

Теорема Гаусса для магнитного поля

Для произвольной замкнутой поверхностиS (рис. 18) поток вектора индукции магнитного поля через эту поверхностьS можно рассчитать по формуле:

.

С другой стороны, число линий магнитной индукции, входящих внутрь объема, ограниченного этой замкнутой поверхностью, равно числу линий, выходящих из этого объема (рис. 18). Поэтому, с учетом того, что поток вектора индукции магнитного поля считается положитель­ным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток Ф_B вектора индукции через произвольную замкнутую поверхность S равен нулю, то есть:

,

что составляет формулировку теоремы Гаусса для магнитного поля.