metodichka

В формулах (16) и (17) значение площади следует брать по модулю. Рассмотренный метод дает самые точные результаты, однако его

применение требует проведения непосредственных измерений на местности.

Графический метод определения площади. Метод заключается в том,

что данные для вычисления площадей простейших фигур берутся с картографического материала (с учетом его масштаба). Если фигура представляет собой многоугольник, то его разбивают на простые фигуры, обычно треугольники. При этом, для повышения точности, разбивку выполняют два-три раза на разные треугольники и за окончательное значение принимают среднюю площадь из нескольких измерений. При разбивке сложных многоугольников следует стремиться, чтобы они, по возможности, не были остроугольными, а ближе были к равносторонним

преимуществом этого способа перед рассмотренными выше является то, что он позволяет определять площади участков земной поверхности практически любой формы (фигур, имеющих криволинейные контуры). Для этого используются различные палетки, ротометры, механические и электронные планиметры.

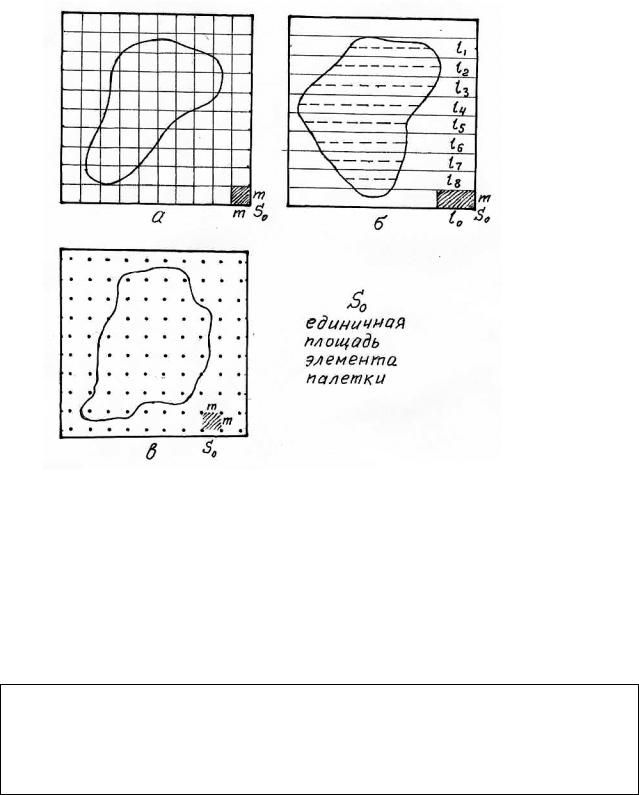
Определение площадей с помощью палеток. Принцип определения площади с помощью палетки пояснен на рис. 34. Палетка представляет собой прозрачную основу, на которой нанесены сетка квадратов с известной стороной (квадратная палетка – рис. 34 а), серия параллельных линий с известным расстоянием между ними (линейная палетка – рис. 34 б), упорядоченная группа точек с известными расстояниями между ними (точечная палетка – рис. 34 в).

При использовании квадратной палетки для данного картографического материала определяют площадь элементарной ячейки (квадрата). Например, сторона квадрата равна 5 мм, масштаб карты 1:10000. В этом случае сторона квадрата на местности будет равна 50 м, а площадь – 2500 м2. Палетку накладывают произвольно на фигуру и определяют число полных квадратов (N) и число всех неполных квадратов (n). Площадь определяют по формуле

S0 = 2500 м2).

Похожий принцип реализуется и при использовании линейной палетки. Только в качестве единичной площади здесь выступает элементарная полоса длиной lo , например, 1 см при известном расстоянии а между линиями. В пределах контура фигуры измеряют длины линий посредине между нанесенными на палетку параллельными линиями, суммируют их и переводят через значение S0 в площадь. Например, S0 (1 см) = 5000 м2,

52

суммарное значение измеренных отрезков L = 28,4 см, S = 28,4 х 5000 = =142000 м2.

Рис. 34. Виды палеток

а – квадратная; б – линейная; в – точечная

При использовании точечной палетки определяют площадь зоны влияния каждой точки, которая, вообще говоря, равна площади квадрата, как и в квадратной палетке. В контуре подсчитывают число точек (N) и умножают его на значение элементарной площади. При этом рекомендуется не принимать во внимание точки, совпадающие с контуром измеряемой площади. Например, S0 = 2500 м2, N = 57, S = 57 х 2500 = 142500 м2 (с учетом площади треугольника внизу фигуры).

Для повышения точности площадь определяют несколько раз (5 – 6 раз) с произвольной перестановкой используемой палетки в любое положение в том числе и с поворотом относительно ее первоначального положения. За окончательное значение площади принимают среднее арифметическое из результатов измерений.

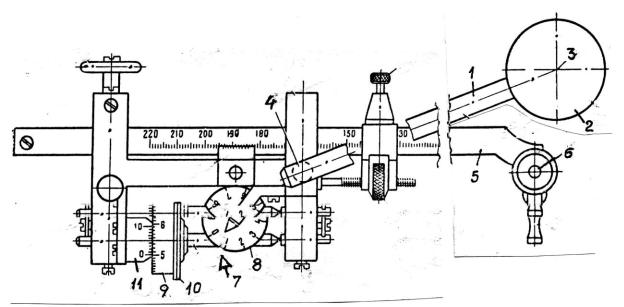
Определение площадей с помощью планиметра. Планиметр (рис. 35) –

это механический прибор, состоящий из полюсного рычага 1 с грузиком 2. Грузик содержит в центре иглу 3 для закрепления его в устойчивом

положении на столе. На другом конце полюсного рычага имеется сферическая шарнирная головка, которая свободно вставляется в гнездо 4 обводного рычага 5. На обводном рычаге имеется обводной штырь 6

53

(обводная марка) и счетный механизм 7. Счетный механизм имеет дисковую шкалу 8 счета оборотов, счетное колесо 9, один оборот которого соответствует одному делению дисковой шкалы. Внешний ободок 10 счетного колеса скользит по бумаге и за счет трения проворачивается и приводит в движение через червячную передачу дисковую шкалу. Со шкалой счетного колеса сопряжена шкала нониуса 11, по которой берут отсчет дробной части наименьшего деления шкалы счетного колеса.

Рис. 35. Планиметр

1- полюсный рычаг; 2 – грузик; 3 – игла; 4 – гнездо; 5 – обводной рычаг; 6 – обводной штырь (обводная марка); 7 – счетный механизм; 8 – дисковая шкала; 9 – счетное колесо; 10 – ободок счетного колеса; 11 – нониус.

Полный отсчет содержит четыре значащих цифры: 1-я – отсчет по шкале диска (5); 2-я – подписанное число на дисковой шкале до нулевого индекса нониуса (7); 3-я – число полных наименьших делений от ближайшей по возрастанию подписанной цифры счетного колеса до нулевого индекса нониуса (3); 4-я – ближайшее от нулевого индекса нониуса деление, совпадающее с делением шкалы счетного колеса (4); таким образом, отсчет равен 5734.

Измерение площади фигуры выполняется в следующей последовательности.

1.Установить планиметр на карте таким образом, чтобы при обводе фигуры угол между полюсным и обводным рычагом не был меньше 30о и больше 150о. При этом колесо счетного механизма обязательно должно перемещаться по поверхности бумаги. Если фигура большая, т.е. не обеспечивается поставленное выше условие, то ее следует измерять по частям. После подбора установки планиметра закрепить полюс нажатием на грузик и в дальнейшем при измерениях не смещать.

2.Установить обводную иглу в точку фигуры с известной площадью (примерно в том же месте, что и измеряемая площадь; такой фигурой может

54

быть квадратная сетка системы прямоугольных координат карты) и взять начальный отсчет Ао по шкалам счетного устройства (например, Ао = 5783).

3.Аккуратно обвести фигуру с известной площадью с возвращением в

Со = 5783 – 5648 = 135; С = 4277 – 4203 = 74.

Вычислить площадь фигуры. Предположим, что известная площадь Sо (Sо = 4 км2), тогда S = (Sо С) : Со.

В приведенном примере: S = (4 км2 * 74) : 135 = 2,193 км2.

Отношение Sо / Со = μ – называется ценой деления планиметра. Таким образом, S = μС.

Для повышения точности измерений площадь определяют несколько раз по схеме, приведенной выше. Целесообразно обвод площадей (известной и неизвестной) выполнять по часовой и против часовой стрелки, т.е. один полный прием измерения площади будет заключаться в двойном измерении. Обычно достаточно двух полных приемов. Окончательное значение площади находят как среднее арифметическое из результатов полных приемов измерений.

Если планиметр содержит два отсчетных устройства, то достаточно выполнить один полный прием, но при использовании во всех случаях двух отсчетных устройств, т.е. по каждой из точек брать по два отсчета, например, Ао1, Ао2, Во1, Во2, А1, А2 и т.д.

11. Основные принципы и методы топографической съемки местности

Как было сказано выше, картографической информацией является только та информация, которая, помимо своего содержания, несет и сведения о пространственных координатах точек определенного объекта или явления. Например, получены размеры строения, которое в заданном масштабе определяется положениями его углов. Для картографического изображения, кроме того, необходимы сведения о координатах данных углов строения. Только в этом случае указанный объект может быть отображен на карте или плане, только в этом случае можно говорить о взаимосвязи этого объекта с другими, составляющими картографическое изображение. То же самое относится и к фиксированным точкам какого-либо явления. Предположим, что на местности были взяты пробы грунта на содержание химически опасного вещества. Для построения картографического изображения зоны загрязнения необходимо знание результатов исследования проб, а также мест их взятия, определяемых координатами в принятой системе координат. В этом случае указанные точки могут быть нанесены на карту (план), и на

55

основе этого полученное картографическое изображение явления может быть проанализировано со всех позиций, определяющих решение поставленной задачи.

11.1. Государственная геодезическая сеть. Сети сгущения. Съемочные сети

Для получения плановых координат и высот точек объектов и явлений , происходящих на физической поверхности Земли и в ее недрах используется Государственная геодезическая сеть (ГГС). ГГС – это система точек,

определенным образом закрепленных на поверхности Земли, для которых с высокой степенью точности известны плановые координаты и абсолютные высоты. ГГС подразделяется на четыре класса точности: I, II, III и IV. Самый точный из них – I-й класс. В необходимых случаях производят сгущение сети прокладкой на местности сетей сгущения 1-го и 2-го разрядов (по точности). Привязку (определение координат точек сетей сгущения) выполняют к пунктам ГГС.

Для привязки точек объектов и явлений на местности прокладывают системы теодолитных ходов, виды и форма которых определяется конкретными задачами съемки. Теодолитный ход – это система закрепленных на поверхности Земли точек (долговременного или кратковременного использования), координаты которых определяют в процессе привязки к пунктам ГГС, либо к пунктам сетей сгущения.

Теодолитные ходы бывают нескольких видов : разомкнутый, замкнутый, диагональный, висячий, свободный.

Разомкнутый теодолитный ход. На рис. 36 а представлена схема разомкнутого теодолитного хода, опирающегося на два исходных направления: AВ и СD, определяемых положениями пунктов А, В, С и D.

Для азимутальной привязки (определения дирекционных углов) линий теодолитного хода, определения координат и высот его точек измеряют:

примычные углы 1, 2,; горизонтальные углы 1, 2 , . . . в вершинах теодолитного хода; наклонные расстояния S и углы наклона ( по принятому направлению хода, например, (В - 1 - 2 - . . . - С ).

Обратите внимание на то, что в принятом направлении хода горизонтальные углы в его вершинах, как это отмечено на рисунке, являются правыми по ходу (при движении в принятом направлении правые горизонтальные углы остаются с правой руки, левые – с левой).

Разомкнутые теодолитные ходы используются при топографической съемке сравнительно узких полос местности, например, при трассировании дорог, линий связи и др. При съемке больших площадей прокладывают несколько разомкнутых теодолитных ходов с узловыми точками в сочетании с замкнутыми, диагональными, висячими теодолитными ходами.

Замкнутый теодолитный ход удобно использовать при съемке небольших площадей примерно округлой формы.

56

Рис. 36. Виды теодолитных ходов

а – разомкнутый; б,в – замкнутые; г – диагональный и висячий; д – свободный замкнутый; е – свободный разомкнутый; А, В, ... – пункты Государственной геодезической сети; 1, 2, 3, ... – вершины теодолитных ходов.

-- - - - - принятое направление хода

Привязка замкнутого теодолитного хода может быть выполнена по двум исходным направлениям с непосредственным включением в вершину многоугольника пункта В Государственной геодезической сети (рис. 36 б) или точки с известными прямоугольными координатами, либо прокладкой дополнительного (подходного) хода от исходных точек (группы пунктов ГГС) - рис. 36 в . В первом случае (рис. 36 б) дирекционный угол передается на сторону 1-2 с помощью двух примычных углов 1 и 2, во втором (рис. 36 в) - с помощью нескольких, например, трех 1, 2, 3, как это следует из схемы теодолитного хода.

При выбранном направлении хода могут быть измерены правые или левые по ходу горизонтальные углы. На схемах - правые углы являются внутренними углами многоугольника, левые – примычные углы в принятом

57

направлении хода. S (i-1)i и (i-1)i - соответственно наклонные расстояния и углы наклона линий теодолитных ходов (в том числе и ходов, являющихся подходными ).

Диагональный ход (рис. 36 в) используют в тех случаях, когда с основного, обычно замкнутого теодолитного хода, невозможно произвести съемку всей территории. Диагональный ход (2 – 7 - 5) опирается на линии теодолитного хода, и его привязка осуществляется с помощью измеренных горизонтальных углов, например, 1 и 2. Для надежного контроля выполняют измерение и других примычных углов ( 3 и 4 ), что фактически приводит к схеме разомкнутого теодолитного хода. При этом требования к точности диагонального хода несколько ниже, чем к точности основного.

Висячий теодолитный ход (2-8-9-10: рис. 36 в) прокладывают в труднодоступных местах. Обычно его используют на застроенной территории при съемках в глухих дворах, для съемки закрытых от основного хода точек.

Следует обратить внимание на то, что висячий теодолитный ход, в отличие от рассмотренных выше (разомкнутого, замкнутого и диагонального ходов), не обеспечивает полного контроля результатов измерений и вычислений, В связи с этим необходимо быть весьма внимательным при производстве работ и при вычислениях, особенно в тех случаях, когда углы , например, в точках 8 и 9 близки к 1800.

Свободный теодолитный ход. Преимущественно рекомендуется использовать замкнутый свободный теодолитный ход (рис. 36 д) , поскольку в нем обеспечивается сравнительно надежный контроль измерений и вычислений и надежная оценка точности по сумме измеренных внутренних или внешних углов, суммам приращений координат и т.п. Разомкнутый cвободный теодолитный ход (рис. 36 г) полностью не обеспечивает контроля измерений и вычислений.

Вычисление координат и высот точек свободных теодолитных ходов выполняют в условной системе, часто с привязкой по магнитному меридиану.

Используют свободные ходы в тех случаях, когда не имеется необходимости в получении координат в принятой системе. Например, при использовании полученного плана для решения локальной задачи составления проекта вертикальной планировки, проекта реконструкции какого-либо инженерного сооружения и т.п. В этих случаях достаточно только ориентирования плана по магнитному азимуту.

11.2. Прямая и обратная геодезические задачи

Прямая и обратная геодезические задачи используются при азимутальной привязке теодолитных ходов и при определении координат их точек.

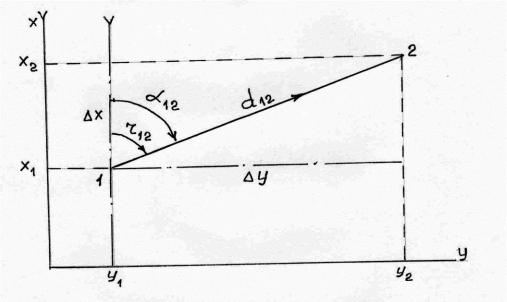
Прямая геодезическая задача имеет следующее содержание: известны прямоугольные координаты точки 1 (рис. 37), дирекционный угол

58

направления 1-2 и расстояние (горизонтальное проложение) между точками 1 и 2; следует определить прямоугольные координаты точки 2.

Рис. 37. Прямая и обратная геодезические задачи

Очевидно, что в зависимости от величины дирекционного угла значения приращений координат будут иметь разные знаки, т.е. координаты точки 2 могут оказаться меньше или больше координат точки 1 при вычислениях их по формулам

Практически решение прямой геодезической задачи сводится к определению приращений координат Х и У:

где d12 – горизонтальное проложение линии 1-2; 12 – дирекционный угол линии 1-2.

Пример

Решение прямой геодезической задачи Известны координаты точки 1: Х1 = 3456,826 м; У1 = 5620,227 м. Известен

дирекционный угол направления 1-2 : 12 = 255º 34,7'. Горизонтальное проложение линии 1-2 d12= 185,347 м. Определить координаты точки 2.

Х= 185,347 cos 255º 34,7' = - 46,162 м

У= 185,347 sin 255º 34,7' = - 179,507 м Х2 = 3456,826 + (- 46,162) = 3410,664 м

У2 = 5620,227 + (- 179,507) = 5440,720 м

Обратная геодезическая задача. Содержание задачи: известны прямоугольные координаты X и Y точек 1 и 2 (рис. 37); необходимо найти дирекционный угол направления 1-2 и горизонтальное проложение между точками 1 и 2.

Принцип решения обратной геодезической задачи заключается в следующем.

59

Для определения дирекционного угла направления 1-2 следует вычислить

и румбовое значение данного направления.

Румб линии – это острый угол (см. раздел 9), заключенный между направлением линии и ближайшим направлением меридиана; румбы имеют название по основным сторонам света: северо-восточный (СВ), северозападный (СЗ), юго-восточный (ЮВ), юго-западный (ЮЗ). На рис. 19 показана взаимосвязь между значениями румбов и дирекционных углов

знака).

Переход от значения румба к дирекционному углу производится с использованием табл. 2 по полученным в формулах (23) и (24) знакам приращений координат.

Горизонтальное проложение из решения обратной геодезической задачи находят по формуле (по теореме Пифагора, см. рис. 37):

П р и м е р

Решение обратной геодезической задачи

Дано: Х = 5937,426 м; У = 4842,039 м; Х = 3142,426 м; У = 6012,483 м.

Определить дирекционный угол направления АВ (и обратный ему дирекционный угол направления ВА) и расстояние между точками А и В.

60

11.3. Взаимосвязь дирекционных углов с горизонтальными углами, измеренными на местности

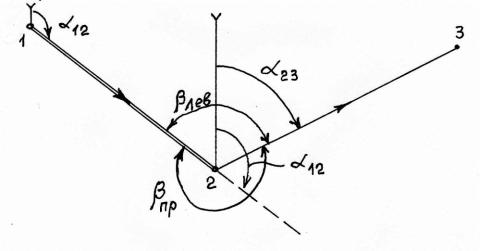
Для передачи дирекционного угла с линии на линию на местности в точке поворота измеряют правый или левый по ходу горизонтальный угол (см. рис. 38).

Рис. 38. Взаимосвязь дирекционных углов с горизонтальными углами, измеренными на местности

Если измерен правый по ходу дирекционный угол (βпр), то дирекционный угол последующей стороны (линии) вычисляют по формуле

В формулах (27) и (28) значения дирекционных углов могут получиться отрицательными, в пределах 0о – 360о или больше 360о. В этом случае к отрицательному значению дирекционного угла следует прибавить 360о, из углов, больших 360о следует вычесть 360о, т. е. В любом случае дирекционный угол необходимо привести к значению в пределах 0о – 360о.

11.4. Определение прямоугольных координат точек теодолитного хода

Для решения поставленной задачи необходимо знать (прямые или обратные) дирекционные углы исходных направлений. При этом достаточно определить дирекционный угол только прямого или только обратного направления, поскольку

ОБР = ПРЯМ

Дирекционные углы исходных направлений находят из решения

обратной геодезической задачи.