
metodichka
.pdf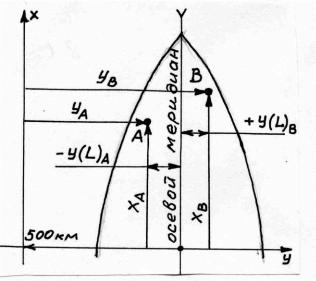
31
8.2. Зональная система прямоугольных координат Гаусса
Поскольку каждая из проекций Гаусса-Крюгера передает на плоскость только фрагмент поверхности Земли, ограниченный меридианами через 6° долготы, то всего на поверхность Земли должно быть составлено 60 проекций (60 зон). Счет зон ведется от Гринвичского меридиана на восток: 1, 2, 3, … и т. д. Каждая зона совпадает по своему положению с границами колонны, номер которой определяет номенклатуру карты с учетом пояса, имеющего буквенное обозначение (см. раздел 10.1 Разграфка и номенклатура топографических карт). Чтобы получить номер зоны,
необходимо из номера колонны вычесть 30, если номер колонны больше 30, и прибавить 30, если номер колонны меньше 30. В каждой из 60 проекций образуется отдельная система прямоугольных координат.
Рис. 19. Зональная система прямоугольных координат Гаусса
Осью Х зональной системы координат Гаусса является осевой меридиан зоны, отнесенный на запад на 500 км (рис. 19). Осью У является проекция экватора, перпендикулярная оси Х. В самой зоне точка может находиться на восток или запад от осевого меридиана на расстоянии L. Для восточной части зоны значения L положительные, для западной –
отрицательные. Связь между координатой У и значением L следующая: |
|
У = 500 км + L |
(3) |
Для указания принадлежности точки определенной зоне впереди координаты У приписывают номер соответствующей зоны.
Например, точка А расположена на расстоянии 5257 км от экватора и на расстоянии L = 82 км к западу от осевого меридиана 15-й зоны. В этом случае координаты точки А будут следующие: ХА = 5257 км, УА = 15418 км (418 = 500 – 82; запись читается так: 418 км в 15-й зоне). Для определения номера зоны по координате У необходимо влево отложить три позиции
полных километров. Оставшееся впереди значение |
укажет номер зоны. |
Например, У = 16627, 544 км – 16-я зона 627,544 км; |
У = 5381625 м – 5-я |
32
зона 381625 м (381,625 км). Первая цифра в координате У после номера зоны не может быть нулем и девяткой.
8.2.1. Вычисление плоских прямоугольных координат Гаусса по географическим координатам
Плоские прямоугольные координаты Гаусса Х и У весьма сложно связаны с географическими координатами λ и φ точек земной поверхности.
Предположим, что некоторая точка А имеет географические координаты λ и φ. Поскольку разность долгот граничных меридианов зоны равна 6°, то соответственно для каждой из зон можно получить долготы крайних меридианов: 1-я зона (0° – 6°), 2-я зона (6° – 12°), 3-я зона (12° – 18°) и т.д. Таким образом, по географической долготе точки А можно определить номер зоны, в которой эта точка находится. При этом долгота λ оn осевого меридиана зоны определится по формуле λ оn = (6°n – 3°), в которой n – номер зоны.
Для определения плоских прямоугольных координат Х и У по географическим координатам λ и φ воспользуемся формулами, выведенными для территории России для референц-эллипсоида Красовского (референцэллипсоид – фигура, максимально приближенная к фигуре Земли в той ее части, на которой находится данное государство, либо группа государств):
Х 6367558,4969( рад) {ao [0,5 (a4 a6l 2 )l 2 ]l 2 N}sin cos |
(4) |
У (L) [1 (a3 a5l 2 )l 2 ]lN cos |
(5) |
В формулах (4) и (5) приняты следующие обозначения: У(L) – расстояние от точки до осевого меридиана зоны;
l = (λ - λo) / (разность долгот определяемой точки и осевого меридиана зоны в радианной мере; = 206264,8062 - число секунд в одном радиане);
φ рад = φ / (широта точки, выраженная в радианной мере);
N = 6399698,902 - 21562,267 – (108,973 – 0,612 cos2 φ) cos2 φ cos2 φ; ао = 32140,404 - 135,3302 – (0,7092 – 0,0040 cos2 φ) cos2 φ cos2 φ;
а3 = (0,3333333 + 0,001123 cos2 φ) cos2 φ – 0,1666667; а4 = (0,25 + 0,00252 cos2 φ ) cos2 φ – 0,04166;
а5 = 0,0083 - 0,1667 - (0,1968 + 0,0040 cos2 φ) cos2 φ cos2 φ; а6 = (0,166 cos2 φ – 0,084) cos2 φ.
Значения широт и долгот по указанным формулам вычисляют до 0,0001 , а значения координат Х и У - до 0,001 м.
По формуле (5) значение координаты У(L) получают относительно осевого меридиана зоны, т.е. оно может получиться со знаками «плюс» для восточной части зоны или «минус» – для западной части зоны. Для записи координаты У в зональной системе координат необходимо вычислить расстояние до точки от осевого меридиана зоны, отнесенного на запад на 500 км, а впереди полученного значения приписать номер зоны. Например, получено значение У(L) = - 303678,774 м в 47 зоне. Тогда
У = 47 (500000,000 – 303678,774) = 47196321,226 м.
33
Пример вычисления плоских прямоугольных координат по геодезическим координатам приведен в разделе 8.2.2.
8.2.2. Вычисление географических координат по плоским прямоугольным координатам Гаусса
Для решения данной задачи также используются формулы пересчета, полученные для референц-эллипсоида Красовского.
Предположим, что нам необходимо вычислить географические координаты φ и λ точки А по ее плоским прямоугольным координатам Х и У, заданным в зональной системе координат. При этом значение координаты У записано с указанием номера зоны и с учетом переноса осевого меридиана зоны на запад на 500 км.
Предварительно по значению У находят номер зоны, в которой расположена определяемая точка, по номеру зоны определяют долготу λ o осевого меридиана и по расстоянию от точки до отнесенного на запад осевого меридиана находят расстояние У(L) от точки до осевого меридиана зоны (последнее может быть со знаком плюс или минус).
Значения географических координат φ и λ по плоским прямоугольным
координатам х и у находят по формулам: |
|
φ = φ х - 1 - ( b4 – 0,12 z2) z2 z2 b2 |
(6) |
λ = λ o + l |
(7) |
l = 1 – ( b3 - b5 z2) z2 z |
(8) |
Вформулах (6) и (8) :
φx = + 50221746 + 293622 + (2350 + 22cos2 )cos2 cos2 10-10sin cos ;
= ( Х / 6367558,4969) ; z = У(L) / ( Nx сos φ x );
Nx = 6399698,902 - 21562,267 – (108,973 – 0,612 cos2 φ x) cos2 φ x cos2 φ x; b2 = (0,5 + 0,003369 cos2 φ x ) sin φ x cos φ x ;
b3 = 0,333333 – ( 0,166667 – 0,001123 cos2 φ x ) cos2 φ x ; b4 = 0,25 + (0,16161 + 0,00562 сos2 φ x) cos2 φ x ;
b5 = 0,2 – (0,1667 – 0,0088 сos2 φ x) cos2 φ x .
Пример вычисления плоских прямоугольных координат Гаусса по географическим координатам и географических координат по плоским прямоугольным координатам Гаусса приведен в таблице 1. При определении координат обязательно выполняется расчет по обратному определению географических координат с целью подтверждения правильности выполненных расчетов. Т.е., если определяются прямоугольные координаты по географическим, то, используя полученные значения прямоугольных координат, необходимо вычислить географические координаты. Они должны совпасть с первоначальными. И наоборот, при вычислении географических координат по прямоугольным следует обратным расчетом проверить значения прямоугольных координат.

34
Пример
Вычислить прямоугольные координаты точки (с обратным контрольным расчетом), имеющей географические координаты λ = 65о01'38,2456" и φ = 47о02'15,0543" и находящейся в 11-й зоне (табл. 1).
Таблица 1 Вычисление плоских прямоугольных координат Х и У по географическим
координатам φ и λ (с обратным перерасчетом)
№№ |
|
Вычисление Х и У |
|
Вычисление φ и λ по |
п/п |
Параметр |
по φ и λ |
Параметр |
Х и У |
|
|
(значение |
|
(значение |
|
|
параметра) |
|
параметра) |
1 |
φ° |
47о02'15,0543" |
βРАД |
0,818760380 |
|
|
|
|
|
2 |
φ" |
169335,0543" |
β" |
168881,4511" |
|
|
|
|
|
3 |
φ"/ρ" |
0,820959510 |
β° |
46о54'41,4512" |
|
|
|
|
|
4 |
Sin φ |
0,731800091 |
Sin β |
0,730299573 |
|
|
|
|
|
5 |
Cos φ |
0,681519352 |
Cos β |
0,683127026 |
|
|
|
|
|
6 |
Cos2 φ |
0,464468627 |
Cos2 β |
0,466662533 |
|
|
|
|
|
7 |
lo |
+2о01'38,2456" |
φ х РАД |
0,821272741 |
8 |
l"/ ρ" |
+0,035382893 |
φ х" |
169399,6627" |
9 |
N |
6389707,353 м |
φ х° |
47о03'19,6628" |
10 |
ао |
32077,69996 |
Sin φ х |
0,732013528 |
11 |
а4 |
0,075000799 |
Cos φ х |
0,681290096 |
12 |
а6 |
-0,003204001 |
Cos2 φ х |
0,464156195 |
13 |
а3 |
-0,011601574 |
Nx |
6389714,058 м |
14 |
а5 |
-0,026270237 |
Nx Cos φ х |
4353248,903 м |
15 |
l2 |
0,001251949 |
z |
+0,035394247 |
|
|
|
|
|
16 |
N l2 |
7999,587730 м |
z2 |
0,001252753 |
|
|
|
|
|
17 |
Х |
5213504,617 м |
φ |
47о02'15,0541" |
|
|
|
|
|
18 |
У(L) |
+154079,966 м |
lо |
+2о01'38,2456" |
|
|
|
|
|
19 |
У |
11654079,966 м |
λ |
65о01'38,2456" |
Примечания:
1. Во второй части таблицы не приведены значения коэффициентов b.
2.Расхождения в значениях φ, равное 0,0002" можно считать допустимым, поскольку ошибка в определении координаты Х в этом случае составляет примерно 7 мм (1" дуги примерно соответствует 33 м).
8.3. Система высот
Высота точки является третьей координатой точки на поверхности Земли и в ее недрах. Рассмотренные ранее системы координат (географических и прямоугольных) относятся к плановым системам, которые
35
не определяют полностью положение точки на физической поверхности Земли.
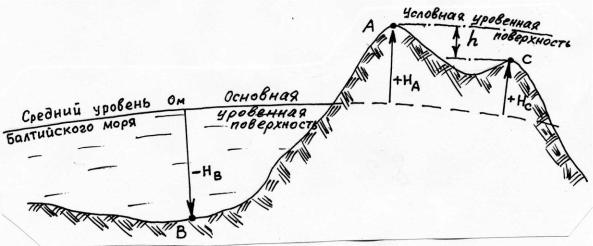
В России принята Балтийская система высот. За нулевую высоту принят средний уровень Балтийского моря. Условно уровень моря продолжен под материками, и для определения высоты точки на суше или на морском дне необходимо определить расстояние по отвесной линии в данной точке до уровня Балтийского моря. Эти расстояния называют абсолютными высотами (рис. 20). Абсолютная высота Н считается положительной, если точка находится дальше от центра Земли, чем уровень Балтийского моря, и отрицательной, если точка находится по отношению к уровню моря со стороны центра Земли.
Рис. 20. Система высот. Абсолютные и относительные высоты
Часто определяют высоты точек не в абсолютной, а относительной форме, по отношению к какой-либо другой точке с известной или неизвестной высотой. Такие высоты называют относительными высотами или превышениями. Превышения обозначают буквой h.
Превышение – это разность абсолютных (или условных) высот двух точек: hС = НС – НА. Оно может быть положительным или отрицательным (а также и равным нулю). Так, в соответствии с рис. 20, превышение точки С над точкой А – отрицательное, а превышение точки А над точкой С – положительное.
Условная высота может быть назначена для какой-либо точки на поверхности Земли, и высоты всех других точек в этом случае определяются относительно нее. Для перевода в Балтийскую систему высот необходимо определить высоту исходной точки в этой системе и перевычислить высоты всех других точек введением соответствующей одинаковой поправки.
8.4. Системы полярных координат
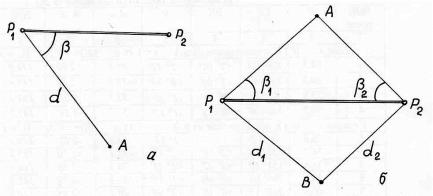
Для полярной системы координат характерно наличие полюса Р1, полярной оси Р1 Р2, полярного угла β между направлением полярной оси и направлением на определяемую точку, расстояния d (горизонтального
36
проложения – проекции линии местности на горизонтальную плоскость) – рис. 21 а.
Полярные углы обычно отсчитывают от полярной оси по направлению движения часовой стрелки.
В биполярной системе координат (рис. 21 б) имеется два полюса (Р1 и Р2), а положение точки однозначно определяется значениями двух горизонтальных углов β1 и β2, измеренных в точках полюсов (угловая засечка), либо значениями двух измеренных горизонтальных проложений d1 и d2 (линейная засечка). В том и другом случаях положение полюсов известно, т.е. известно и расстояние между ними.
Рис. 21. Полярные системы координат
Указанные системы координат часто используют для получения координат точек местности при производстве топографической съемки. Засечка точек производится с известных на местности базисов, для концов которых отдельно определяют координаты, а также определяют дирекционный угол направления базиса.
9. Ориентирование направлений
Ориентировать линию – это значит определить ее направление относительно исходного, заданного или известного направления.
В качестве исходных направлений используют направления истинного (географического) меридиана, направление осевого меридиана зоны и направление магнитного меридиана.
Магнитный меридиан – это линия пересечения с поверхностью Земли плоскости, образованной осью магнитной стрелки компаса и направлением линии силы тяжести в данной точке.
Ориентирующим углом в общем случае называется горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления исходного меридиана до направления ориентируемой линии.
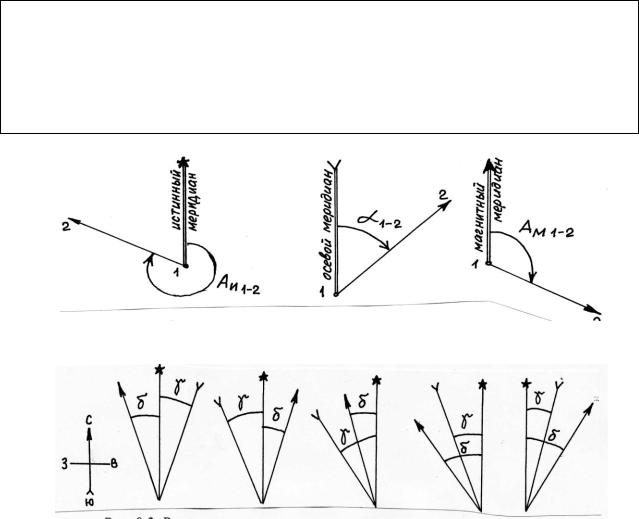
Ориентирующий угол, отсчитываемый от северного направления истинного меридиана, называется истинным (географическим) азимутом (АИ), см. рис. 22.
Дирекционный угол (α) отсчитывают от северного направления осевого меридиана (оси Х прямоугольной системы координат Гаусса).
37
Магнитный азимут отсчитывают от северного направления магнитного меридиана (АМ).
Ориентирующие углы изменяются от 0° до 360°. В расчетах могут получиться отрицательные значения ориентирующих углов, либо значения, большие 360°. Всегда необходимо стремиться к тому, чтобы ориентирующий угол принимал значение в пределах от 0° до 360°. Для этого к отрицательным значениям ориентирующих углов необходимо прибавить 360°, а из значений ориентирующих углов, больших 360°, необходимо вычесть 360°.
Рис. 22. Ориентирующие углы
Рис. 23. Взаимосвязь ориентирующих углов
Если полученный ориентирующий угол назвать прямым, то обратный ориентирующий угол будет отличаться от прямого на 180° (и наоборот), т.е.,
АОБР = АПР |
+ |
180° |
(9) |
АПР = АОБР |
+ |
180° |
(10) |
Вформулах (9) и (10) перед 180° всегда можно оставлять знак «плюс».
Вобщем случае в каждой точке на физической поверхности Земли существуют три исходных ориентирующих направления (некоторые возможные варианты представлены на рис. 23).
Формулы взаимосвязи следующие:
АИ = α + γ |
(11) |
АИ = АМ + δ , |
(12) |
где γ – сближение меридианов; δ – магнитное склонение.
Сближение меридианов и магнитное склонение могут быть восточными - положительными и западными – отрицательными.
Если осевой меридиан отклонен на восток от истинного, то сближение меридианов – положительное, т.е. точка находится в восточной части зоны. И
38
наоборот, если он отклонен на запад, то точка находится в западной части зоны и сближение меридианов для нее будет отрицательным.
Если магнитный меридиан отклонен от истинного на восток, то магнитное склонение будет восточным, если на запад, то западным.
Сближение меридианов можно с достаточно высокой точностью (до 0,1
угловых минуты) определить по формуле: |
|
γ = Δλ Sin φ , |
(13) |
где Δλ = λi – λо ; λi – долгота точки, λо – долгота осевого меридиана зоны; φ – географическая широта точки. Значение Δλ удобно при расчетах превратить в минуты, а затем полученную величину γ выразить в градусах и минутах.
В связи с тем, что магнитные полюсы Земли находятся в постоянном движении, в расчетах при решении задач по ориентированию используют величину годового изменения магнитного склонения Δδ, которое используют для перевычисления магнитного склонения, известного на год t1, к году t2 :
δt2 = δt1 + Δδ (t2 – t1) |
(14) |
Годовое изменение магнитного склонения также может быть восточным и западным (соответственно положительным и отрицательным).
Решим общую задачу на ориентирование линий в аналитическом и графическом (рис. 18) виде.
Исходным ориентирующим углом в задаче является дирекционный угол, что обычно и имеет место при работе с топографическими картами, поскольку измерить на карте легче именно его без дополнительных построений.
Пример
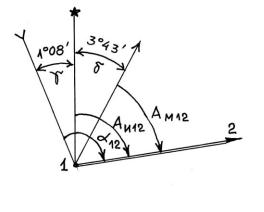
Задача на ориентирование линий Исходные данные. Известен дирекционный угол направления 1-2 α1-2 = 36°48', долгота
точки 1 восточная λ1 = 19°39', широта точки 1 северная φ1 = 57°04', магнитное склонение на 1991 г. δ91 = 4°16' (восточное), годовое изменение магнитного склонения Δδ = 0°03' (западное).
Определить истинный азимут направления 1-2 (АИ 1-2) и магнитный азимут направления
1-2 на 2002 г. (АМ 1-2).
Рис. 24. К примеру : ориентирование линий
Решение. 1. Определяем значение сближения меридианов для точки 1. По значению долготы для точки 1 находим, что она расположена в 4-й зоне , долгота осевого меридиана которой равна 21°. Следовательно, γ1 = Δλ1 Sin φ1 = (λ1 - λо) Sin φ1 = (19°39' -21°00')
39
Sin 57°04' = ( - 1°21') Sin 57°04' = (- 81' ) 0,839304 = - 67,98' = - 68' = - 1°08' (или 1°08' –
западное).
2. Вычисляем магнитное склонение на 2002 г.: δ2002 = δ1991 + Δδ (2002 – 1991) = =+ 4°16' + (-0°03') 11 = +4°16' - 0°33' = + 3°43' (или 3°43' – восточное).
3. |
Вычисляем истинный азимут: АИ 1-2 = α1-2 + γ1 = 36°48' + ( - 1°08') = 35°40'. |
4. |
Вычисляем магнитный азимут на 2002 г.: АМ = АИ - δ = 35°40' - (+3°43') = |
= 31°57'.
Эта же задача легко решается и графически. Предварительно выполняются вычисления по пп. 1 и 2, а затем строится сетка меридианов (рис. 24) с определяемым направлением 1-2: относительно истинного меридиана осевой меридиан отклонен на запад на 1°08', а магнитный меридиан в 2002 г. отклонен относительно истинного на восток на 3°43'. По схеме легко находятся определяемые величины, соответствующие полученным в пп. 3 и 4.
Кроме рассмотренной выше круговой системы ориентирования
используется четвертная система ориентирования, в которой указывается направление в соответствии со сторонами света (рис. 25).
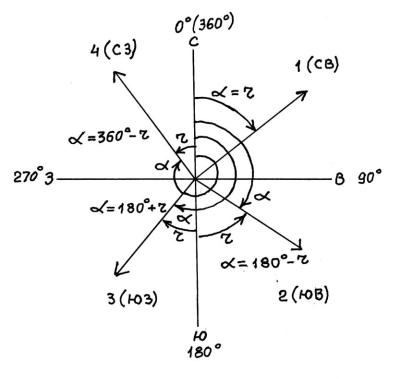
Рис. 25. Четвертная (румбовая) система ориентирования
Величина угла (румб линии – r) определяется острым углом между направлением линии и ближайшим направлением меридиана. Значение румба может находиться в пределах от 0о до 90о. Для обозначения четверти впереди значения румба приписывают название четверти: СВ, ЮВ, ЮЗ, СЗ.
Взаимосвязь между румбами дирекционных углов и самими дирекционными углами показана на рис. 25. Аналогичная взаимосвязь существует и для соответствующих румбов истинного и магнитного азимутов. Пересчет же румбов различных ориентирующих углов может быть выполнен через сами ориентирующие углы, либо напрямую с учетом сближения меридианов и магнитного склонения.

40
В качестве иллюстрации взаимосвязи румбов с дирекционными углами рассмотрим несколько примеров.
1. Предположим, что дирекционный угол какого-либо направления равен α = 123о35,4'. По рис. 25 определяем, что движение по указанному направлению производится во второй четверти, следовательно,
r= ЮВ: (180о00,0' – 123о35,4') = ЮВ:56о24,6'.
2.Румб линии r = СЗ:65о58'. Это соответствует четвертой четверти, т.е.
α= 360о00' - 65о58' = 294о02'.
3.Найти меньший угол между направлениями, имеющими румбы СВ:60о и ЮЗ:15о. Дирекционный угол 1-го направления равен значению румба (1-я четверть), дирекционный угол второго направления равен 180о + 15о = 195о. Для этого случая меньший угол между направлениями будет равен 195о – 60о = 135о.
10. Топографические карты
Топографические карты отражают современное с их изучением состояние местности с той полнотой и детальностью, которая определяется масштабом карты. Они являются основным материалом для построения других карт различного назначения, поскольку являются картографическим изображением с максимальным подробным отображением всей имеющейся на поверхности Земли ситуации в зависимости от масштаба карты.
Топографические карты строят только в проекции Гаусса-Крюгера.
Топографические карты можно разделить на два вида: топографические карты суши и топографические карты шельфа и внутренних водоемов. Первые из них являются основными.
По своему содержанию топографические карты суши являются общегеографическими. По назначению они являются универсальными и могут быть использованы во всех областях народного хозяйства, а также в интересах обороны государства. Для их создания используется единая система координат, единый масштабный ряд, единые требования к полноте содержания и характеру оформления.
Для топографических карт принят стандартный ряд масштабов (масштаб карты – степень уменьшения изображения местности):
1 |
: 1 000 000 |
Т о п о г р а ф и ч е с к и е |
к а р т ы |
1 |
: 500 000 |
Карта – уменьшенное изображение значительных по размеру |
|
1 |
: 200 000 |
участков земной поверхности, построенное с учетом кривизны |
|
1 |
: 100 000 |
Земли |
|
1 |
: 50 000 |
|
|
1 |
: 25 000 |
|
|
1 |
: 10 000 |
|
|
1 |
: 5000 |
Т о п о г р а ф и ч е с к и е |
п л а н ы |
1 |
: 2000 |
План – уменьшенное, подобное изображение небольших |
|
1 |
: 1000 |
участков поверхности Земли, построенное в ортогональной |
|
1 |
: 500 |
проекции |
|
