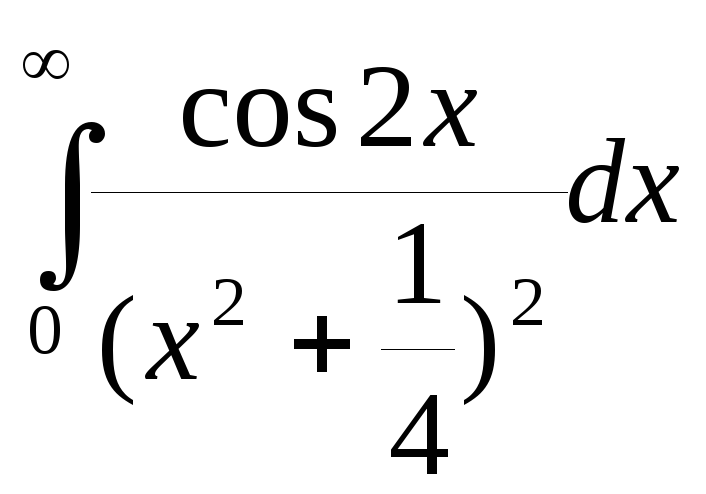Вариант №16

Задание 1.

а) Найти модуль и аргумент чисел =и=. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: ,,.

Задание 2. Вычислить значение функциив точке, ответ представить в алгебраической форме комплексного числа:

а) ,;

б) ,.

Задание 3. Указать область дифференцируемости функциии вычислить производную. Выделить действительную и мнимую часть полученной производной.

Задание 4.Определить вид кривой.

Задание 5.Построить область плоскости, определяемую данными неравенствами.

а) ;

б)

Задание 6. Проверить, может ли функциябыть мнимой частью некоторой аналитической функции, если да – восстановить ее, при условии.

Задание 7.Найти область плоскости, в которую отображается с помощью функцииобласть:плоскости.

Задание 8.Найти все лорановские разложения данной функциипо степеням. Указать главную и правильную части ряда.

а) =,;

б) =,

Задание 9.Функцию=разложить в ряд Лорана в окрестности точки.

Задание 10.Для функциинайти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

а) =;

б) =.

Задание 11. Вычислить интеграл от функции комплексного переменного:

Задание 12.Вычислить интегралы, используя теорему Коши о вычетах.

а) ;

б) .

Задание 13.Вычислить интегралы с помощью вычетов.

1. 

2. 

3. 

4. 

Вариант №17

Задание 1.

а) Найти модуль и аргумент чисел =и=. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: ,,.

Задание 2. Вычислить значение функциив точке, ответ представить в алгебраической форме комплексного числа:

а) ;

б) ,.

Задание 3. Указать область дифференцируемости функциии вычислить производную. Выделить действительную и мнимую часть полученной производной.

Задание 4.Определить вид кривой.

Задание 5.Построить область плоскости, определяемую данными неравенствами.

а) ;

б)

Задание 6. Проверить, может ли функциябыть мнимой частью некоторой аналитической функции, если да – восстановить ее, при условии.

Задание 7.Найти область плоскости, в которую отображается с помощью функцииобласть:плоскости.

Задание 8.Найти все лорановские разложения данной функциипо степеням. Указать главную и правильную части ряда.

а) =,;

б) =,.

Задание 9.Функцию=разложить в ряд Лорана в окрестности точки.

Задание 10.Для функциинайти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

а) =;

б) =.

Задание 11. Вычислить интеграл от функции комплексного переменного:

Задание 12.Вычислить интегралы, используя теорему Коши о вычетах.

а) ;

б) .

Задание 13.Вычислить интегралы с помощью вычетов.

1. 

2. 

3. 

4. 

Вариант №18

Задание 1.

а) Найти модуль и аргумент чисел =и=. Изобразить числа на комплексной плоскости. Представить числа в тригонометрической и показательной форме.

б) Найти: ,,.

Задание 2. Вычислить значение функциив точке, ответ представить в алгебраической форме комплексного числа:

а) ,;

б) ,.

Задание 3. Указать область дифференцируемости функциии вычислить производную. Выделить действительную и мнимую часть полученной производной.

Задание 4.Определить вид кривой.

Задание 5.Построить область плоскости, определяемую данными неравенствами.

а) ;

б)

Задание 6. Проверить, может ли функциябыть действительной частью некоторой аналитической функции, если да – восстановить ее, при условии.

Задание 7.Найти область плоскости, в которую отображается с помощью функцииобласть:плоскости.

Задание 8.Найти все лорановские разложения данной функциипо степеням. Указать главную и правильную части ряда.

а) =,;

б) =,.

Задание 9.Функцию=разложить в ряд Лорана в окрестности точки.

Задание 10.Для функциинайти изолированные особые точки, провести их классификацию, вычислить вычеты относительно найденных точек.

а) =;

б) =.

Задание 11. Вычислить интеграл от функции комплексного переменного:

; АВС – ломаная

Задание 12.Вычислить интегралы, используя теорему Коши о вычетах.

а) ;

б) .

Задание 13.Вычислить интегралы с помощью вычетов.

1. 

2. 

3. 

4.