Рассмотрим уравнение кривой второго порядка общего вида

.(9)

Инвариантом уравнения (9) называют алгебраическое выражение, составленное из коэффициентов при старших членах уравнения (9), которое не изменяется при любом преобразовании координат.

С помощью инварианта определяют принадлежность кривой к определенному типу : 1) если, то уравнение определяет кривую эллиптического типа ; 2) если, то гиперболического типа ; 3) если, то параболического типа.

Так как в уравнении (9) , то оси симметрии кривой не параллельны осям координат. Повернем оси координат так, чтобы они стали параллельны осям симметрии кривой, для этого воспользуемся формулами поворота осей координат (3) :,. Подставим выражения дляв уравнение (9), имеем

.

Раскроем скобки и приведем подобные члены, в новых координатах получаем уравнение

,(10)

где ,

,

,

, .

Выберем угол так, чтобы в новой системе координат оси симметрии были параллельны осям координат, т.е. положим, или

.

Так как , поэтому. После поворота осей координат на этот угол в уравнении (10) исчезнет произведение переменных.

В задании 3 дано уравнение

.

Так как ,, то уравнение определяет кривую гиперболического типа. Приведем его к каноническому виду. Для этого вначале выполним поворот системы координатна угол, для которого; по формулам тригонометрии

, ,находим

, ,и записываем по формулам поворота осей координат (3)

,

.

Подставим выражения ив данное уравнение, получим

.

Раскроем скобки, приведем подобные члены, получим

.

Выполнив параллельный перенос системы координат, приведем это уравнение к каноническому уравнению гиперболы. Для этого сгруппируем слагаемые с одноименными переменными

,

выделим полные квадраты относительно ,

, или

, или

.

Поместим начало новой системы координат в точку, воспользуемся формулами параллельного переноса (2)

, , или, учитывая координаты нового начала,

, , окончательно получим

.(11)

Построим все три системы координат ,,, учитывая, что угол поворота системы

,

а точка в системе координатимеет координаты. В систему координатпоместим кривую (гиперболу), определяемую уравнением (11).

Рис. 6

К заданию 4.

Как известно, пара чисел на плоскости определяет точку, а уравнение, связывающееи, – линию на плоскости. Помимо декартовых, на плоскости можно построить большое число других систем координат. Каждая из систем употребляется там, где это удобнее (и декартова – чаще всех бывает удобной), но при исследовании вращательных движений самой эффективной является полярная система координат.

Рис. 7

Полярная система координат определяется заданием некоторой точки (полюса), исходящего из этой точки луча (полярной оси) и указанием единицы масштаба. Рассмотрим произвольную точку плоскости; обозначим расстояние точкиот полюсачерез, угол, на который нужно повернуть лучдля совмещения его с, черезφ . Угол φ будем понимать так, как это принято в тригонометрии (т.е. углы, получаемые при вращении полярной оси вокруг полюса против часовой стрелки, положительны ; при вращении полярной оси по часовой стрелке – отрицательны). Числа (полярный радиус) иφ (полярный угол) называют полярными координатами точки и записывают. Для того чтобы соответствие между точками плоскости и парами чиселбыло взаимно однозначным, обычно считают, чтои(или.

Запишем формулы, устанавливающие связь декартовых координат с полярными. Из получим

, (12)

а также .

Решение задания 4 а).

Построим линию, заданную уравнением

, где .

Для построения указанной линии составим таблицу значений и(придаваязначения, равные,).

Ввиду четности значениядляодинаковы.

На плоскости построим точки, соответствующие имеющимся в таблице парам чисел и, в выбранной нами полярной системе координат. Соединяя последовательно эти точки, получим линию, называемую кардиоидой (Рис.8).

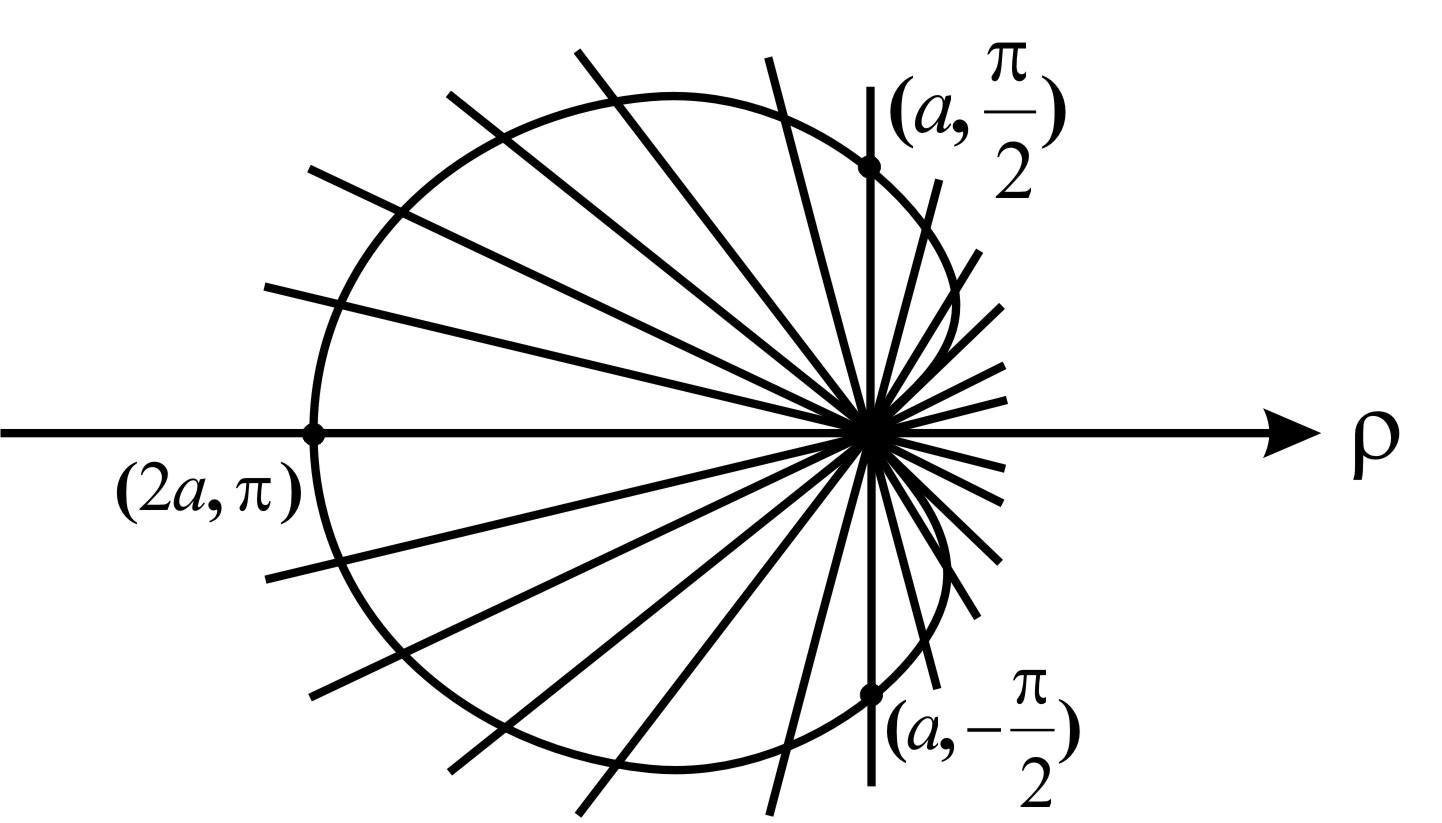
Рис. 8

Решение задания 4 б).