Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Операционное исчисление

Индивидуальные задания

Пособие разработано доцентом Цыловой Е. Г., доцентом Кротовой Е. Л.. Одобрено методической комиссией кафедры «Высшая математика» © 2007, каф. «Высшая математика» ПГТУ

Пермь 2007

Контрольная работа по операционному исчислению

Список литературы.

1. Араманович И.Г., Лунц Г.А., Эльсгольц Л.Э. Функции комплексного переменного. Операционное исчисление. Теория устойчивости.-М.,1965, ч.2,гл.7 - 287 с.

2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. пособие: в 2-х т.- Изд. стер. –М.: Интеграл – Пресс. Т.1. -2001.- 415 с. Т.2.- 2002.- 544 с.

Решение типового варианта.

Контрольная работа

Вариант 0.

Задача 1.Является ли оригиналом функция?

Решение: Данная функция не является оригиналом, так как неравенствоне может выполняться ни при какихsдля всехt>0, так как. , что для любогоsвыполнено неравенство, начиная с некоторого значенияt.

Задача 2. Найти изображения оригинала:

Решение:По таблице изображений найдем:

.

Задача 3. Найти оригиналы, соответствующие изображению:

Решение: Преобразуемтаким образом, чтобы можно было воспользоваться таблицей изображений:

; прежде чем преобразовывать второе слагаемое выделим полный квадрат в знаменателе для того, чтобы воспользоваться свойством линейности преобразования Лапласа:

при построении оригинала, соответствующего третьему слагаемому сначала найдем оригинал для функции , а затем применим теорему запаздывания для оригинала:

Задача 4. Не вычисляя интегралы, найти изображение

Решение: Воспользуемся теоремой об интегрировании оригинала:. И, значит,

Задача 5. Вычислить интеграл

Решение:Интегралпредставляет собой свертку функцийи. Ее изображением согласно теореме о свертке будет функция. Мы привели дробь, представляющую изображения в виде алгебраической суммы дробей таким образом, чтобы для каждой части существовал оригинал в таблице. Тогда убедимся, что оригиналом этого изображения служит следующая функция. И, значит,=.

Задача 6. Найти решение задачи Коши

Решение: Пусть функцияимеет изображение. Тогда по теореме о дифференцировании оригинала получим. Применим преобразование Лапласа к обеим частям уравнения. Выпишем получившееся операторное уравнение. Откуда получим. Таким образом.

Задача 7. Решить систему уравнений

Решение:Пустьи.Учтя, что, получим операторную систему линейных уравнений

Решая систему, получим =. Воспользовавшись таблицей изображений, найдеми.

Задача 8. Решить интегральное уравнение

Решение:Интеграл представляет собой свертку функцийи. Пусть. Тогда по теореме о свертке выпишем изображение интеграла. Составим теперь операторное уравнение, откуда. И, значит,.

Задание 9.Найти изображение функции, заданной следующим графиком:

Решение. Согласно графику функции (обозначим ее через), имеем:

Поэтому ее изображение можно найти, используя формулу преобразования Лапласа:

.

Ответ..

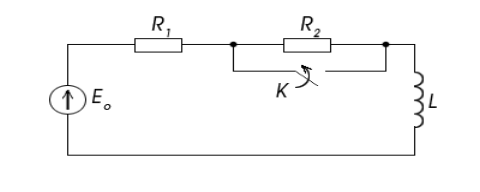
Задание 10. Контур подключен к постоянной э.д.с.(см. рис.) При установившемся режиме включается рубильники накоротко замыкает сопротивление. Найти выражение переходного тока..

Решение. Дифференциальное уравнение Кирхгофа до включения рубильникав данном случае имеет вид:

Согласно постановке задачи . Решим это уравнение операционным методом, предполагая, что.

.

Найдем оригинал получившегося изображения, разложив дроби на простые слагаемые методом неопределенных коэффициентов:

Таким образом, .

Установившийся ток в контуре до включения рубильника есть. Дифференциальное уравнение Кирхгофа после замыкания рубильникаимеет вид:

.

Решим это уравнение операционным методом.

.

Как и в предыдущем случае воспользуемся методом неопределенных коэффициентов для разложения изображения на слагаемые.

Оригиналом получившейся разности, как нетрудно заметить, будет .

Ответ. .