
- •Федеральное агентство по образованию
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Вариант 18
Изменить порядок интегрирования
 .
.Вычислить двойной интеграл
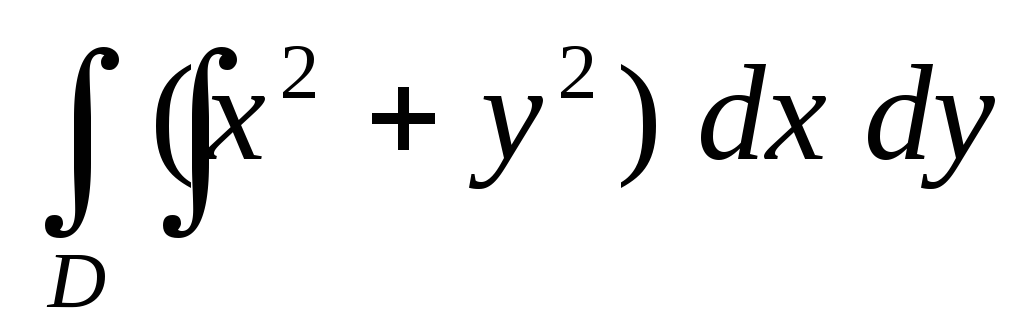 по областиD, ограниченной
линией
по областиD, ограниченной
линией .
.Найти моменты инерции прямоугольника относительно его основания (a) и высоты (h).
Вычислить объем тела V, ограниченного поверхностями
 .
Плотность телаVсчитать
равной единице.
.
Плотность телаVсчитать
равной единице.Вычислить интеграл
 .
.Вычислить тройной интеграл
 ,
если областьVограничена
плоскостями
,
если областьVограничена
плоскостями .
.Найти массу тела, ограниченного поверхностями
 .
.Вычислить криволинейный интеграл первого рода
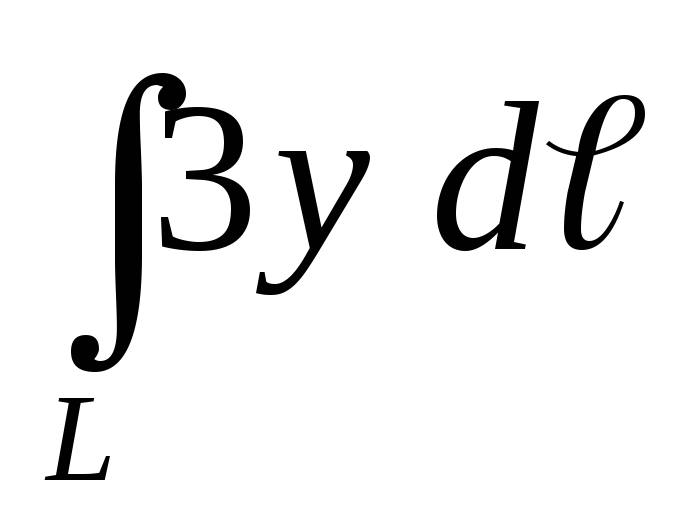 ,
еслиL– дуга кубической
параболы
,
еслиL– дуга кубической
параболы .
.Найти массу кривой
 на
участке от
на
участке от до
до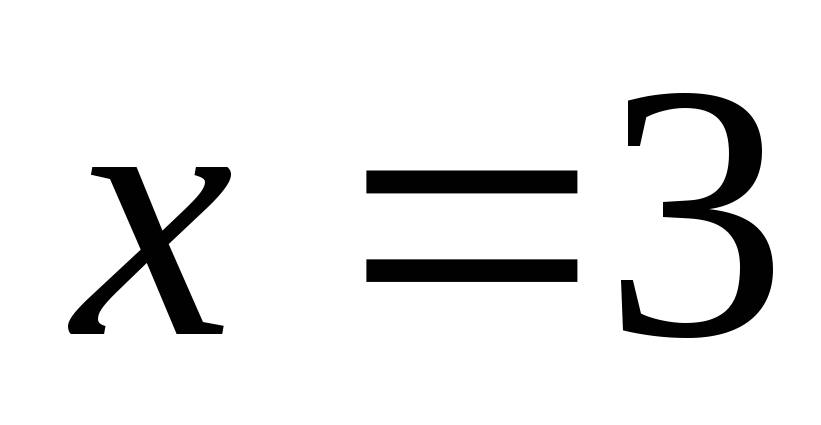 считая, что в каждой точке плотность
обратно пропорциональна ординате этой
точки.
считая, что в каждой точке плотность
обратно пропорциональна ординате этой
точки.Вычислить криволинейный интеграл второго рода
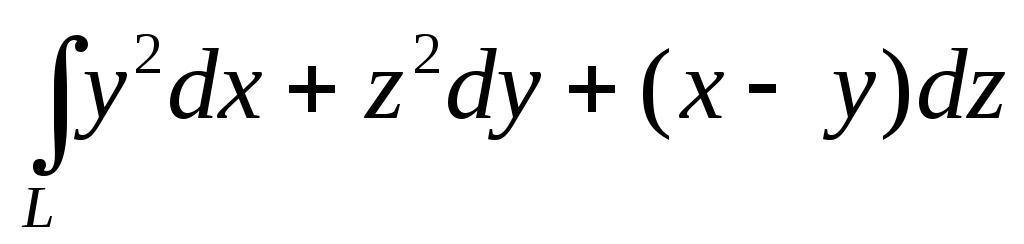 ,
гдеL– отрезок прямой
от точки А(1,0,2) до точки В (2,-1,0).
,
гдеL– отрезок прямой
от точки А(1,0,2) до точки В (2,-1,0).Убедившись, что подынтегральное выражение представляет собой полный дифференциал, вычислить интеграл
 .
.Вычислить поверхностный интеграл первого рода
 по пространственной области
по пространственной области ,
определяемой условиями
,
определяемой условиями .
.Вычислить поверхностный интеграл второго рода
 гдеS– внешняя сторона
эллипсоида
гдеS– внешняя сторона
эллипсоида .
.
Вариант 19
Изменить порядок интегрирования в повторном интеграле
 .
.Вычислить двойной интеграл
 по областиD, ограниченной
линиями
по областиD, ограниченной
линиями .
.Найти моменты инерции
 однородной плоской фигуры относительно
координатных осей. Плоская фигура
ограничена линиями:
однородной плоской фигуры относительно
координатных осей. Плоская фигура
ограничена линиями:

 .
.Вычислить объем тела V, ограниченного поверхностями
 .
Плотность телаVсчитать
равной единице.
.
Плотность телаVсчитать
равной единице.Вычислить интеграл
 .
.Вычислить тройной интеграл
 ,
если областьVограничена
плоскостями
,
если областьVограничена
плоскостями .
.Найти объем тела, ограниченного поверхностями
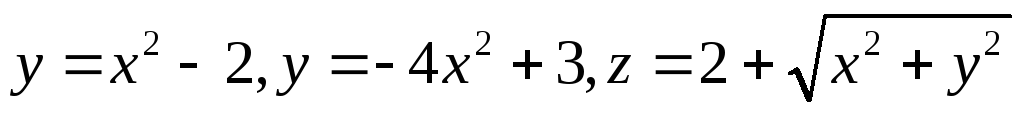 .
.Вычислить криволинейный интеграл первого рода
 ,
еслиL– дуга астроиды
,
еслиL– дуга астроиды .
.Вычислить массу эллипса L, определенного параметрическими уравнениями
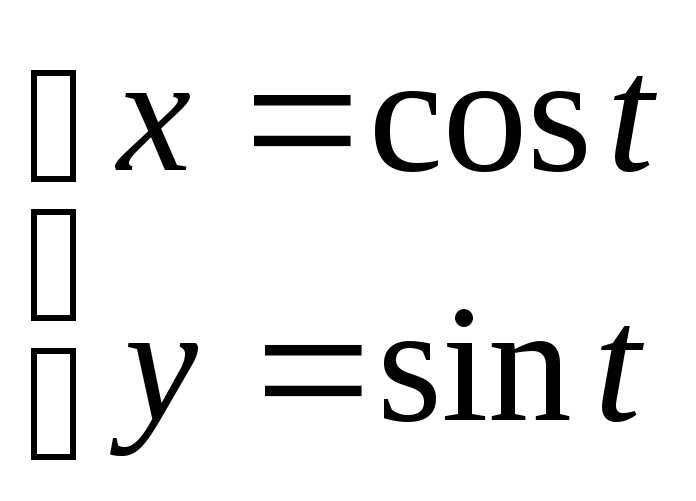
 .
.Вычислить криволинейный интеграл второго рода
 ,
гдеL– дуга параболы
,
гдеL– дуга параболы при
при .
.С помощью формулы Грина вычислить криволинейный интеграл
 ,
еслиL– окружность с
центром в начале координат радиусаR,
пробегаемая в положительном направлении.
,
еслиL– окружность с
центром в начале координат радиусаR,
пробегаемая в положительном направлении.Вычислить поверхностный интеграл первого рода
 по пространственной области
по пространственной области ,
определяемой условиями
,
определяемой условиями .
.Вычислить поверхностный интеграл второго рода
 гдеS– внешняя сторона
эллипсоида
гдеS– внешняя сторона
эллипсоида .
.
Вариант 20
Изменить порядок интегрирования
 .
.Вычислить двойной интеграл
 по областиD, ограниченной
линиями
по областиD, ограниченной
линиями .
.Вычислить массу круга
 ,
если в каждой точке его плотность равна
расстоянию до начала координат.
,
если в каждой точке его плотность равна
расстоянию до начала координат.Вычислить объем тела V, ограниченного поверхностями
 .
Плотность телаVсчитать
равной единице.
.
Плотность телаVсчитать
равной единице.Вычислить интеграл
 .
.Вычислить тройной интеграл
 ,
если областьVограничена
поверхностями
,
если областьVограничена
поверхностями .
.Найти массу тела, ограниченного прямым круговым цилиндром радиуса Rи высотыH, если его плотность в любой точке пропорциональна квадрату расстояния этой точки от центра основания цилиндра.
Вычислить криволинейный интеграл первого рода
 ,
еслиL– дуга кривой
,
еслиL– дуга кривой .
.Найти массу первого витка винтовой линии
 плотность
которой в каждой точке равна квадрату
полярного радиуса этой точки.
плотность
которой в каждой точке равна квадрату
полярного радиуса этой точки.Вычислить криволинейный интеграл второго рода
 ,
гдеL– контур треугольника
АВС с вершинами А(0,0), В(2,0), С(4,2) при
положительном направлении обхода.
,
гдеL– контур треугольника
АВС с вершинами А(0,0), В(2,0), С(4,2) при
положительном направлении обхода.С помощью формулы Грина вычислить криволинейный интеграл
 ,
еслиL– эллипс
,
еслиL– эллипс ,
пробегаемый в положительном направлении.
,
пробегаемый в положительном направлении.Вычислить поверхностный интеграл первого рода
 по пространственной области
по пространственной области
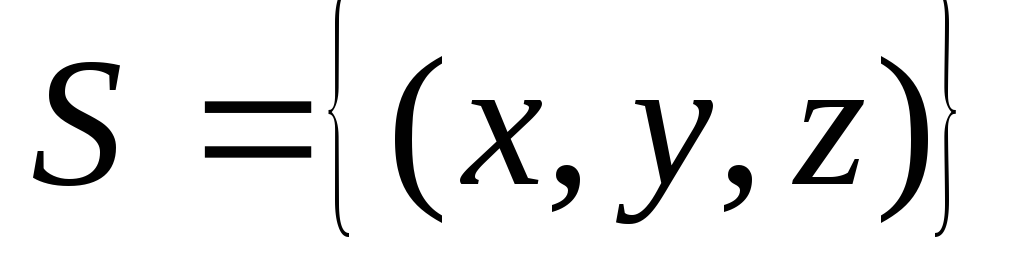 ,
определяемой условиями
,
определяемой условиями .
.Вычислить поверхностный интеграл второго рода
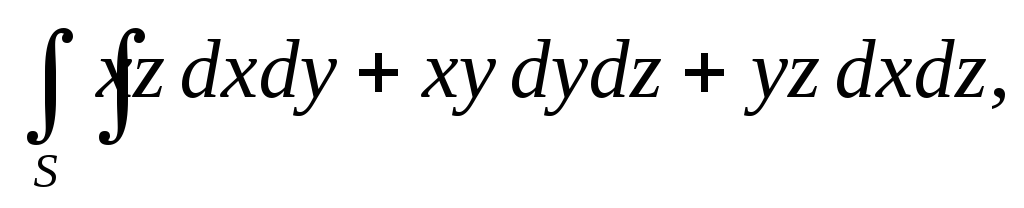 гдеS– внешняя сторона
пирамиды, составленной плоскостями
гдеS– внешняя сторона
пирамиды, составленной плоскостями и
и .
.
