Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кратные, криволинейные и поверхностные интегралы

Индивидуальные задания

Пособие разработано доц. Плаксиной В. П., доц. Макагоновой М. А., ст. преп. Пепеляевой Н.В., ст. преп. Тонкоевой И. В., ст. преп. Скумбиной Т. Н.. Одобрено методической комиссией кафедры «Высшая математика» © 2007, каф. «Высшая математика» ПГТУ

Пермь 2007

Указания к выполнению заданий:

Выполните задания 1-4 с помощью двойного интеграла, задания 5-7 с помощью тройного интеграла, задания 8-11 с помощью криволинейных интегралов, задания 12-13 с помощью поверхностных интегралов.

В каждом задании выполните схематический чертеж.

Вариант 1

1. Изменить порядок интегрирования .

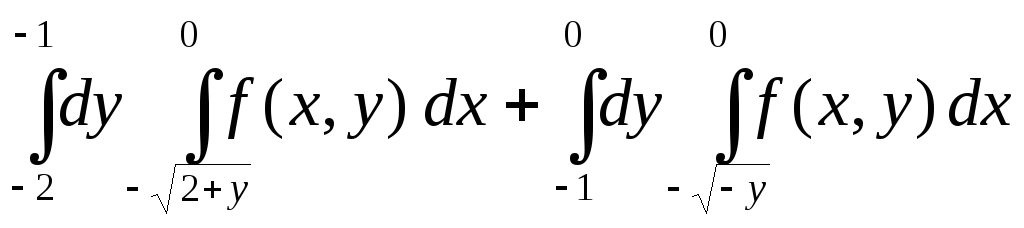2. Вычислить двойной интеграл по областиD, определяемой условиями.

3. Вычислить с помощью двойного интеграла площадь области D, ограниченной кривой .

4. Вычислить с помощью двойного интеграла объем тела V, ограниченного поверхностями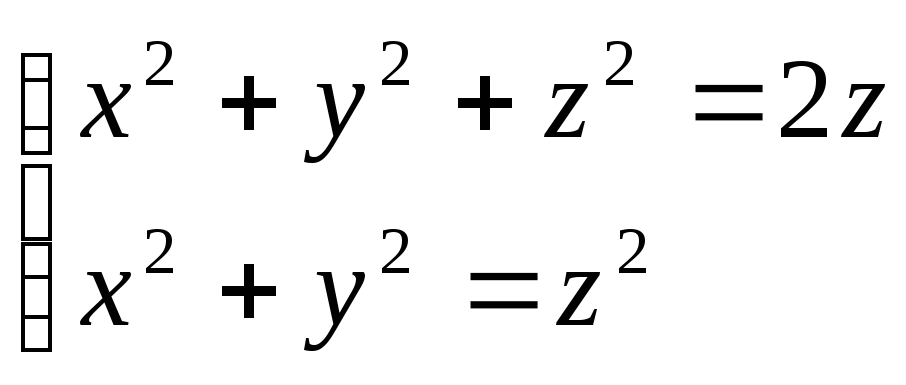. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл 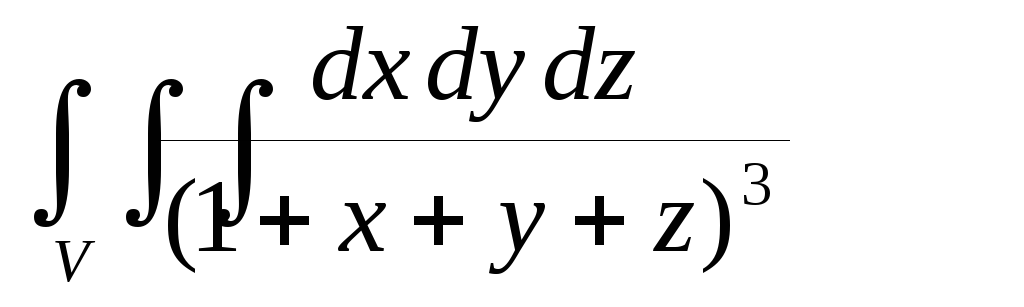по пространственной областиV, ограниченной поверхностями.

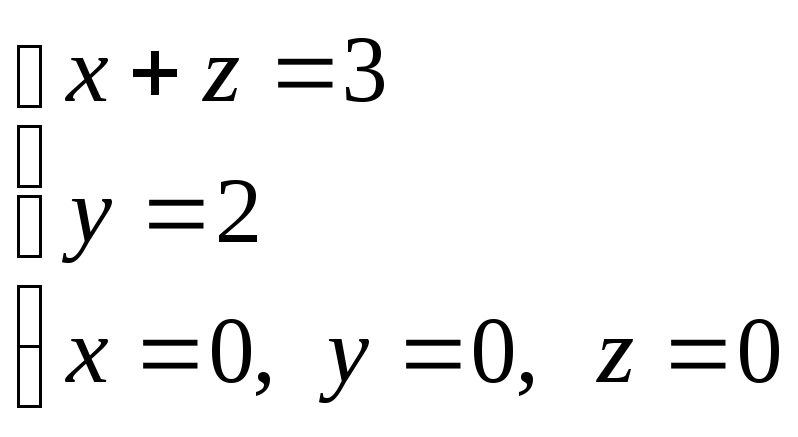6. Вычислить интеграл , если областьVопределяется неравенствами.

7. Вычислить массу тела, ограниченного поверхностью 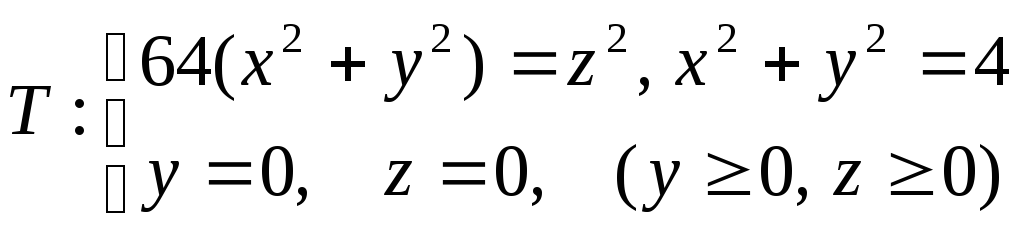и имеющего плотность.

8. Вычислить криволинейный интеграл первого рода , еслиL– дуга окружности.

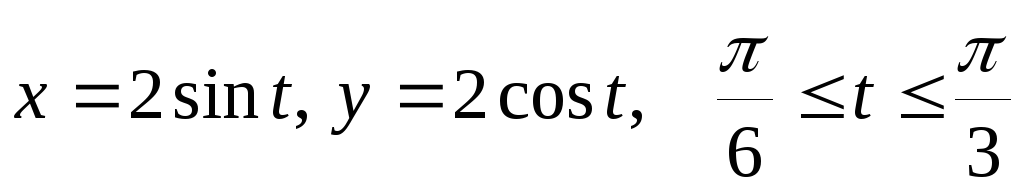9. Найти центр тяжести одной арки циклоиды 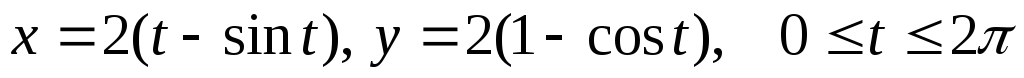, считая плотность равной единице.

10. Вычислить криволинейный интеграл второго рода 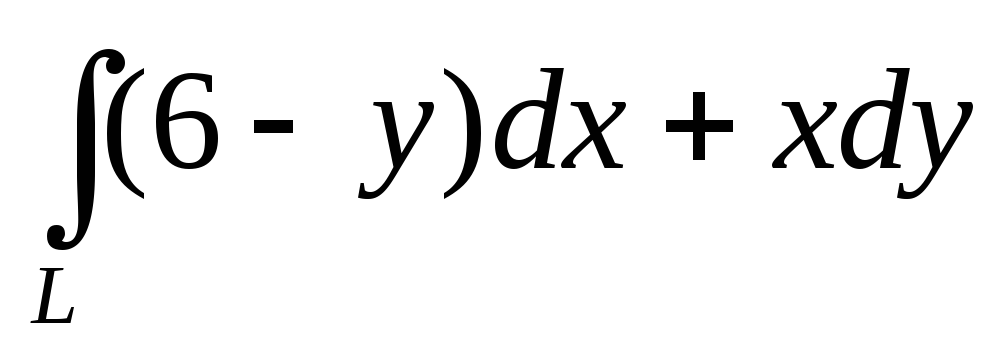, гдеL– арка циклоиды.

11. Вычислить с помощью формулы Грина криволинейный интеграл по окружностиLс центром в начале координат радиусаR, при положительном направлении обхода.

12. Вычислить поверхностный интеграл первого рода по пространственной области, определяемой условиями.

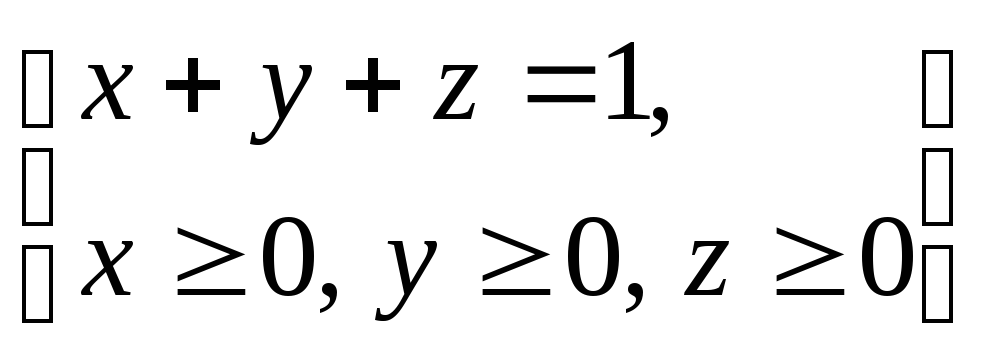13. Вычислить по формуле Стокса криволинейный интеграл , гдеL– окружность, по которой плоскостьпересекает сферу, заданную уравнением.

Вариант 2

1. Изменить порядок интегрирования в повторном интеграле .

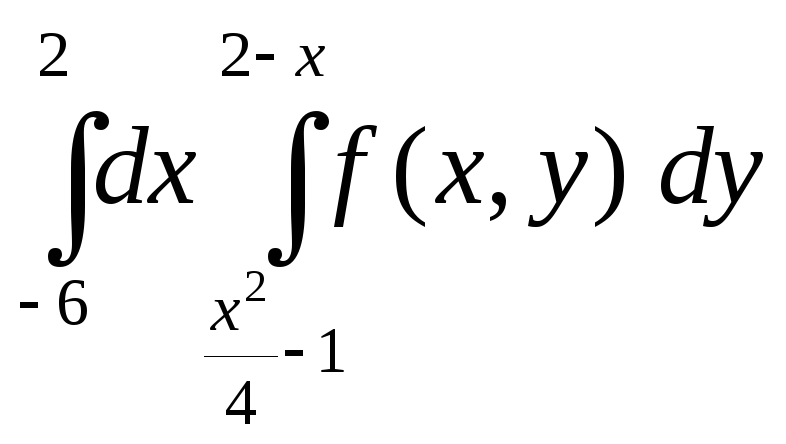2. Вычислить двойной интеграл 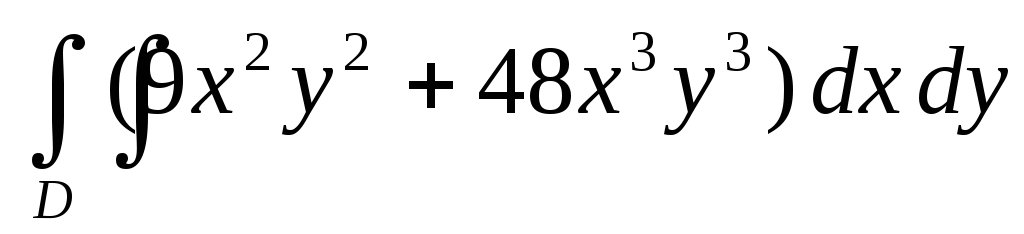по областиD, ограниченной линиями.

3. Вычислить с помощью двойного интеграла площадь области D, определяемой уравнениями.

4. Вычислить объем тела V, ограниченного поверхностями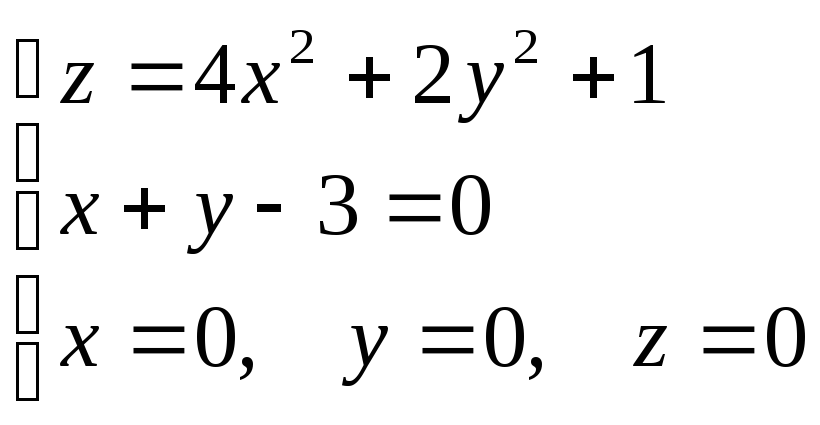. Плотность телаVсчитать равной единице.

5. Вычислить тройной интеграл по пространственной областиV, определяемой уравнениями.

6. Вычислить интеграл , если областьVограничена поверхностями.

7. Найти координаты центра тяжести тела, ограниченного поверхностями: .

8. Вычислить криволинейный интеграл первого рода по кривойL.

9. Определить центр тяжести дуги астроиды , лежащей в первой четверти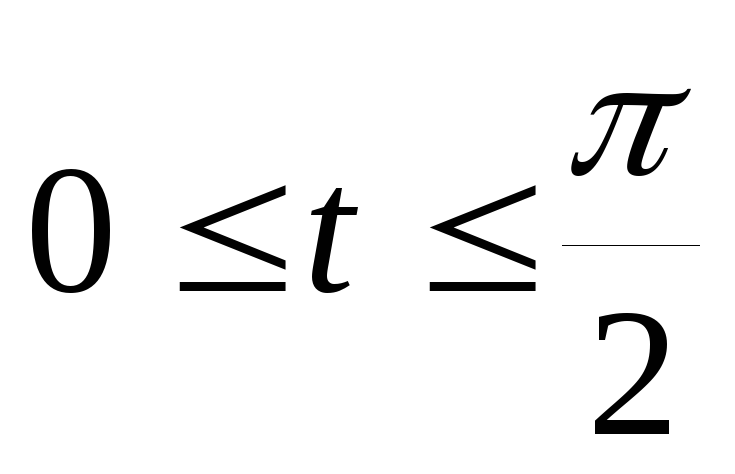. Плотность считать равной единице.

10. Вычислить криволинейный интеграл второго рода 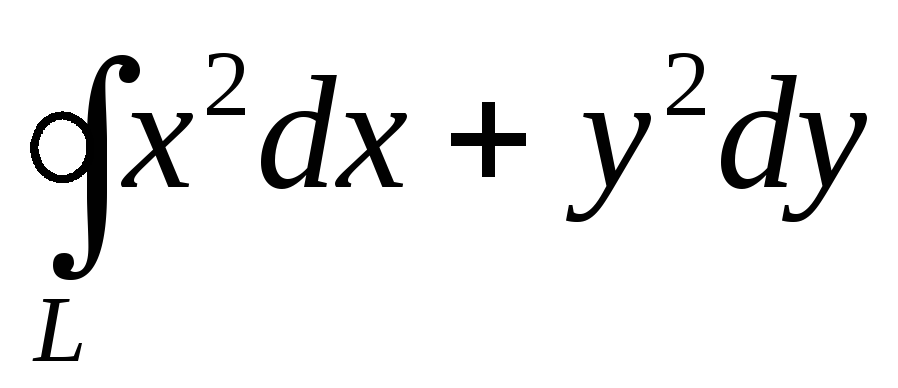, еслиL– контур эллипса, взятый при положительном направлении обхода.

11. Вычислить с помощью формулы Грина криволинейный интеграл 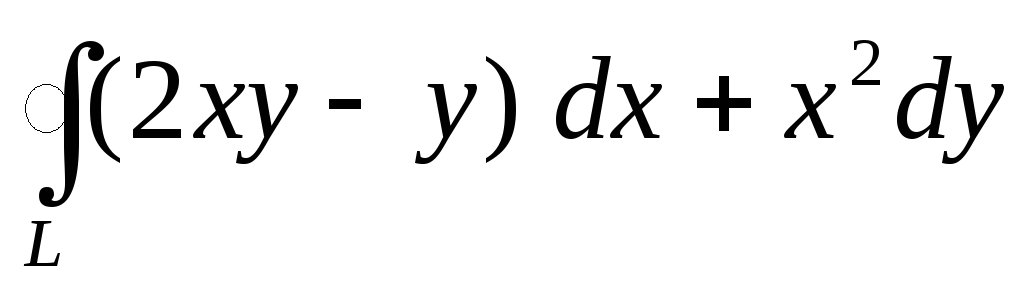по замкнутой кривойL, пробегаемой так, что внутренность ограниченной эллипсом области остается слева.

12. Вычислить поверхностный интеграл первого рода по пространственной области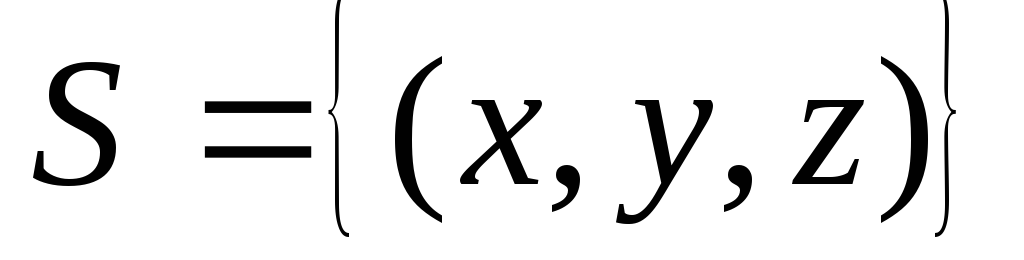, определяемой условиями.

13. Вычислить поверхностный интеграл второго рода , гдеS- внешняя сторона сферы.