
Физика - Оптика
.docОптика
Все действия света характеризуются вектором напряжённости.
Уравнение электромагнитной волны:
![]() .
В прозрачных средах
.
В прозрачных средах
![]() .
Показатель преломления среды
.
Показатель преломления среды
![]() .
Т.к. зависит от
частоты колебаний, то
.
Т.к. зависит от
частоты колебаний, то
![]() .
.
Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе.
Длина волны в среде
![]() ,
где
,
где
![]() – длина волны в вакууме.
– длина волны в вакууме.
Модуль среднего по времени
значения плотности потока энергии,
переносимой волной, называется
интенсивностью волны:
![]() .
Т.к.
.
Т.к.
![]() ,
то
,
то
![]() .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда
![]() .
.
Свет излучается цугами. Каждый цуг
длится порядка
![]() с.
с.
В однородной среде свет распространяется прямолинейно (при отсутствии маленьких отверстий). При пересечении световых лучей они не возмущают друг друга (при не слишком больших интенсивностях).
Отражённый луч лежит в одной плоскости с падающим и с перпендикуляром, восстановленным в точке падения, причём угол падения равен углу отражения.
Закон преломления:
![]() ,
где
,
где
![]() – угол преломления,
– угол преломления,
![]() – скорость в i-й среде,
– скорость в i-й среде,
![]() – преломление i-й
среды.
– преломление i-й
среды.
![]() .
.
Оптическая длина пути
![]() .
.
Принцип Ферма: Свет распространяется по такому пути, оптическая длина которого минимальна.
![]()
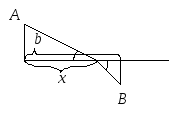
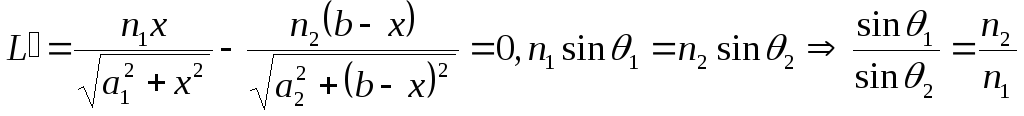 .
.
Интерференция световых волн
П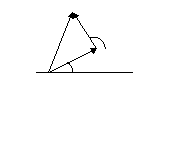 усть
в какую-то точку приходят две волны:
усть
в какую-то точку приходят две волны:
![]() ,
,
![]() .
Тогда амплитуда результирующего
колебания
.
Тогда амплитуда результирующего
колебания
![]() .
Усреднив по времени, получим:
.
Усреднив по времени, получим:
![]() (где
(где
![]() ),
следовательно,
),
следовательно,
![]() .
.
Если разность фаз
остаётся постоянной по времени, то такие
лучи называются когерентными. Тогда
![]() .
.
Явление перераспределения интенсивности называется интерференцией.
Пусть один луч расщепили на два и пустили
их по путям
![]() и
и
![]() .
Тогда у начального луча фаза
.
Тогда у начального луча фаза
![]() ,
у расщеплённых –
,
у расщеплённых –
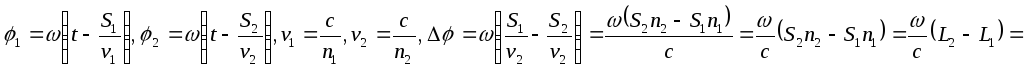
![]() .
Когда оптическая разность хода
.
Когда оптическая разность хода
![]() ,
будет максимум распределения интенсивности,
а когда
,
будет максимум распределения интенсивности,
а когда
![]() ,
будет минимум распределения интенсивности.
,
будет минимум распределения интенсивности.
Интерференция от двух источников
![]()
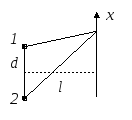 – разность хода. При этом
– разность хода. При этом
![]() .
Оптическая разность хода
.
Оптическая разность хода
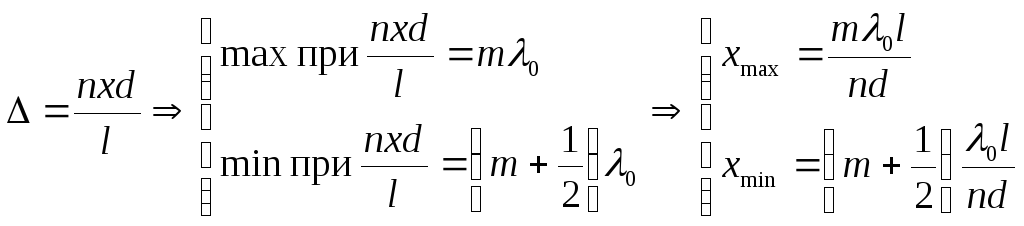 ,
где m – любое целое
число. Отсюда видно, что ширина
интерференционной полосы
,
где m – любое целое
число. Отсюда видно, что ширина
интерференционной полосы
![]() .
.
П усть
распространяются две волны:
усть
распространяются две волны:
![]() ,
,
![]() .
Суммарная волна
.
Суммарная волна
![]()
![]() .
Отсюда видно, что амплитуда суммарного
колебания
.
Отсюда видно, что амплитуда суммарного
колебания
![]() зависит от точки экрана, в которую она
попадает. Если
зависит от точки экрана, в которую она
попадает. Если
![]() ,
то наблюдается максимум, следовательно,
,
то наблюдается максимум, следовательно,
![]() ,
где – угол
между волнами.
,
где – угол
между волнами.
Интерференция на тонких пластинах
О птический
путь левого луча внутри пластинки:
птический
путь левого луча внутри пластинки:
![]() .
Оптический путь правого луча, проходимый
им в то время, пока второй луч идёт внутри
пластинки:
.
Оптический путь правого луча, проходимый
им в то время, пока второй луч идёт внутри
пластинки:
![]() .
Оптическая разность хода:
.
Оптическая разность хода:
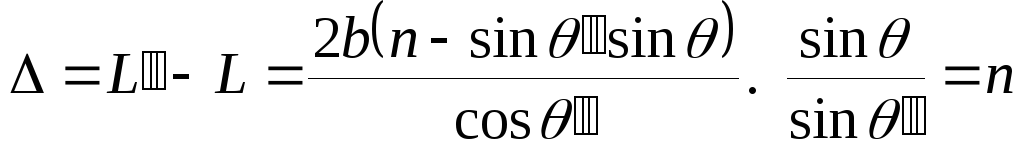 ,
следовательно,
,
следовательно,
![]() .
.
При отражении от границы раздела двух сред, если вторая среда более оптически плотная, то происходит скачок фазы на .
Следовательно,
![]() .
.
Н айдём
айдём
![]() ,
следовательно, оптическая разность
хода
,
следовательно, оптическая разность
хода
![]() .
Если
.
Если
![]() ,
то кольцо светлое. Если
,
то кольцо светлое. Если
![]() ,
то кольцо тёмное.
,
то кольцо тёмное.
Радиус m-го кольца:
![]() .
.
Временная когерентность
Пусть есть цуг, растянутый во временном
промежутке
![]() с амплитудой
с амплитудой
![]() при
при
![]() .
Разложим его в интеграл Фурье:
.
Разложим его в интеграл Фурье:
![]() ,
где
,
где
![]() .
При этом
.
При этом
![]() ,
т.к.
,
т.к.
![]() – нечётная функция, а
– нечётная функция, а
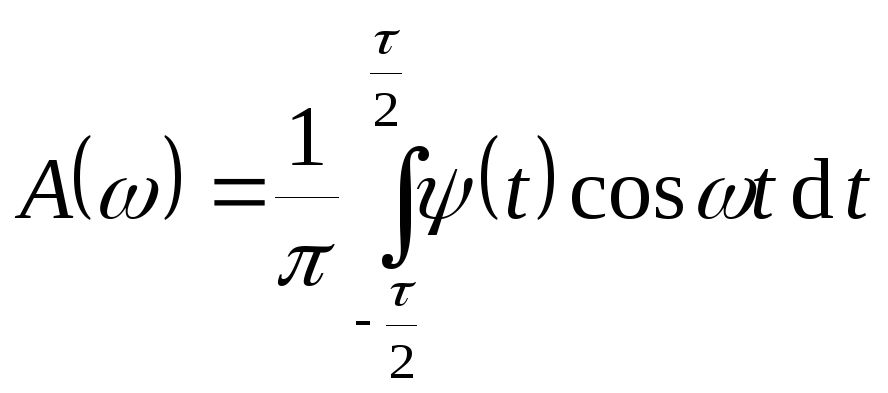 ,
т.к.
,
т.к.
![]() при
при

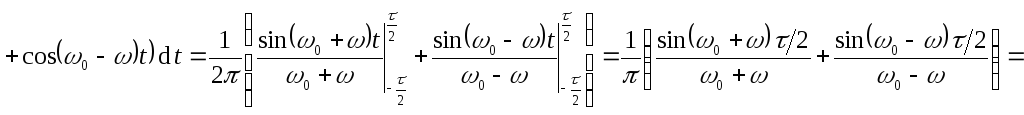
 ,
т.к. и
,
т.к. и
![]() – большие частоты.
– большие частоты.
Интенсивность света
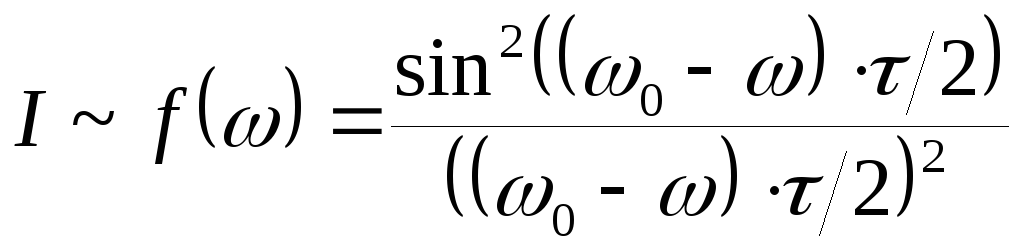 .
.
![]() .
.
В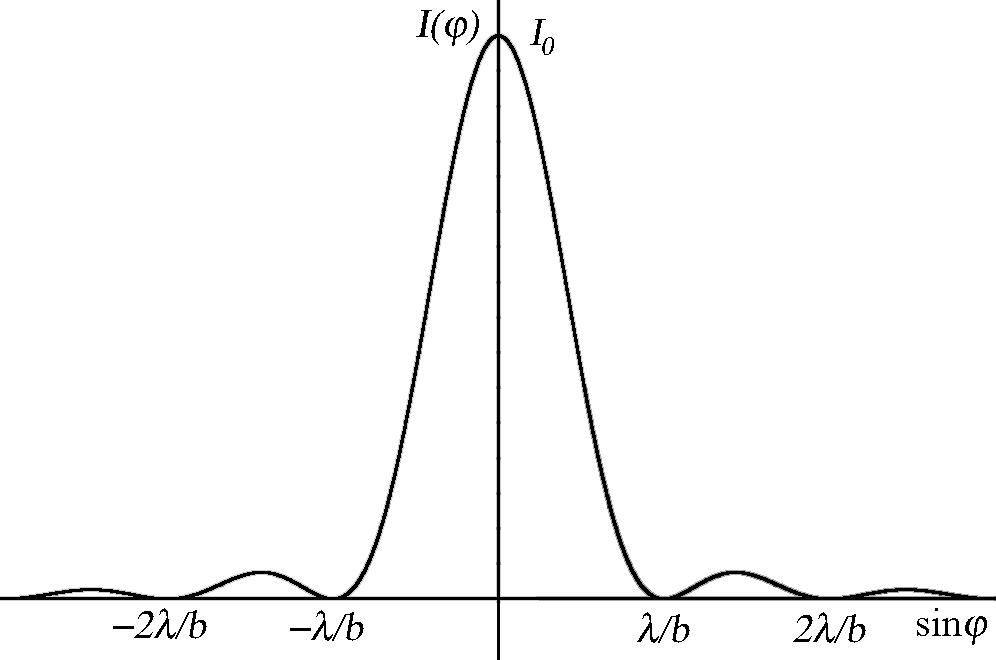 ремя
когерентности – это то время, за которое
случайное изменение фазы колебания
достигнет значения порядка .
ремя
когерентности – это то время, за которое
случайное изменение фазы колебания
достигнет значения порядка .
![]() – длина когерентности – то расстояние,
которое волна проходит за время
когерентности.
– длина когерентности – то расстояние,
которое волна проходит за время
когерентности.
Если оптическая разность хода порядка
![]() ,
то эти два луча становятся некогерентными.
,
то эти два луча становятся некогерентными.
Вернёмся к пластинке:
![]() ,
т.к.
,
т.к.
![]() .
.
Таким образом, толщина b
должна быть порядка
![]() м.
м.
Пространственная когерентность
П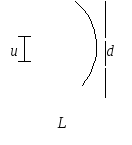 усть
в пространстве распространяется
сферическая волна. Выясним, какое
максимальное расстояние d
между двумя точками на её фронте можно
взять, при котором волна всё ещё будет
когерентна сама себе. Для этого можно
обернуть картину и представить, что
свет, излученный двумя точечными
источниками, находящимися на расстоянии
d попадает в точку с
координатой u. Тогда
оптическая разность хода
усть
в пространстве распространяется
сферическая волна. Выясним, какое
максимальное расстояние d
между двумя точками на её фронте можно
взять, при котором волна всё ещё будет
когерентна сама себе. Для этого можно
обернуть картину и представить, что
свет, излученный двумя точечными
источниками, находящимися на расстоянии
d попадает в точку с
координатой u. Тогда
оптическая разность хода
![]() и если
и если
![]() ,
то волны будут когерентны.
,
то волны будут когерентны.
![]() – ширина когерентности – предельное
расстояние на фронте волны, в двух точках
которого волны ещё когерентны. Угол
когерентности
– ширина когерентности – предельное
расстояние на фронте волны, в двух точках
которого волны ещё когерентны. Угол
когерентности
![]() .
.
Дифракция
П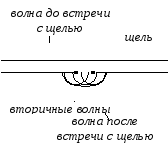 ринцип
Гюйгенса: Каждая точка
волнового фронта является источником
вторичных волн, а огибающая этих вторичных
волн есть новое положение фронта волны.
ринцип
Гюйгенса: Каждая точка
волнового фронта является источником
вторичных волн, а огибающая этих вторичных
волн есть новое положение фронта волны.
Принцип Гюйгенса-Френеля: Амплитуда вторичной волны пропорциональна площади элемента, который её испускает.
Уравнение волны, испущенной площадкой
![]() ,
где – угол
между нормалью к площадке и направлением,
в котором рассматривается излучение,
,
где – угол
между нормалью к площадке и направлением,
в котором рассматривается излучение,
![]() – коэффициент, введённый Френелем,
– коэффициент, введённый Френелем,
![]() ,
,
![]() – фаза колебания в точке на поверхности
фронта. Уравнение всего волнового
фронта:
– фаза колебания в точке на поверхности
фронта. Уравнение всего волнового
фронта:
![]() ,
где S – его площадь
(например, на рисунке это площадь щели).
,
где S – его площадь
(например, на рисунке это площадь щели).
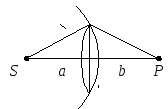
Зоны Френеля
З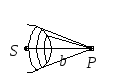 оны,
ограниченные точками с расстоянием от
волнового фронта до точки P,
равном
оны,
ограниченные точками с расстоянием от
волнового фронта до точки P,
равном
![]() ,
называются зонами Френеля.
,
называются зонами Френеля.
Разность фаз у соответствующих волн из разных зон Френеля равна .
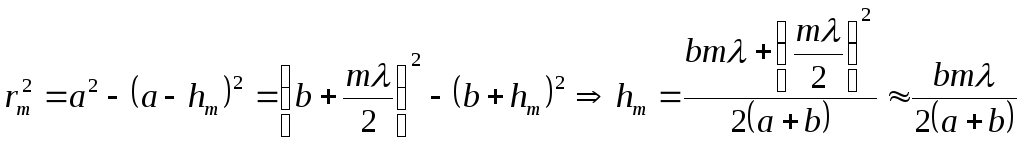 .
.
Площадь сегмента
![]() .
Площадь зоны
.
Площадь зоны
![]() .
.
Е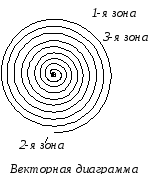 сли
углы очень малы, то
сли
углы очень малы, то
![]() .
Тогда амплитуда колебаний в точке P
.
Тогда амплитуда колебаний в точке P
![]() ,
где
,
где
![]() – амплитуда колебания, приходящего из
i-й зоны Френеля;
– амплитуда колебания, приходящего из
i-й зоны Френеля;
![]() ,
т.к.
,
т.к.
![]() .
.
Радиус m-й зоны
![]() .
.
Количество зон, открываемых отверстием
радиуса
![]() .
.
Дифракция Фраунгофера
Т ак
как, согласно принципу Гюйгенса-Френеля,
амплитуда пропорциональна площади
излучающей поверхности, а она в случае,
изображённом на рисунке, пропорциональна
ширине отрезка, лежащего в щели, то
ак
как, согласно принципу Гюйгенса-Френеля,
амплитуда пропорциональна площади
излучающей поверхности, а она в случае,
изображённом на рисунке, пропорциональна
ширине отрезка, лежащего в щели, то
![]() .
Амплитуда приходящей волны
.
Амплитуда приходящей волны
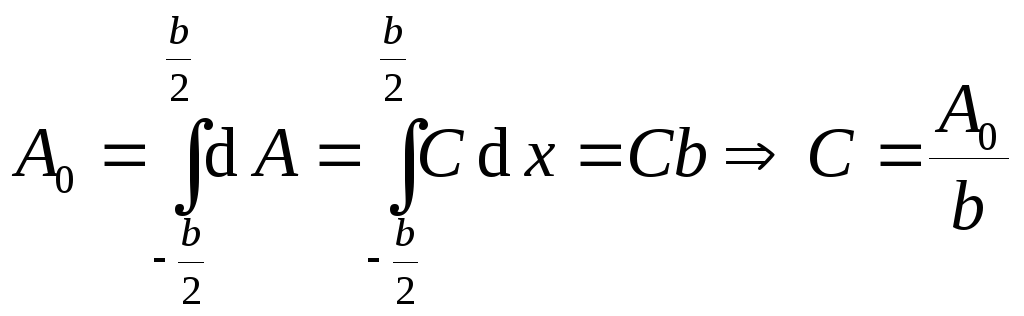 .
.
Разность хода
![]() ;
сдвиг фазы
;
сдвиг фазы
![]() .
.
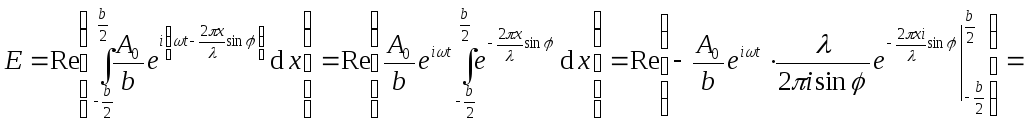
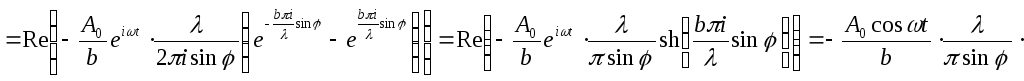
![]() .
Интенсивность
.
Интенсивность
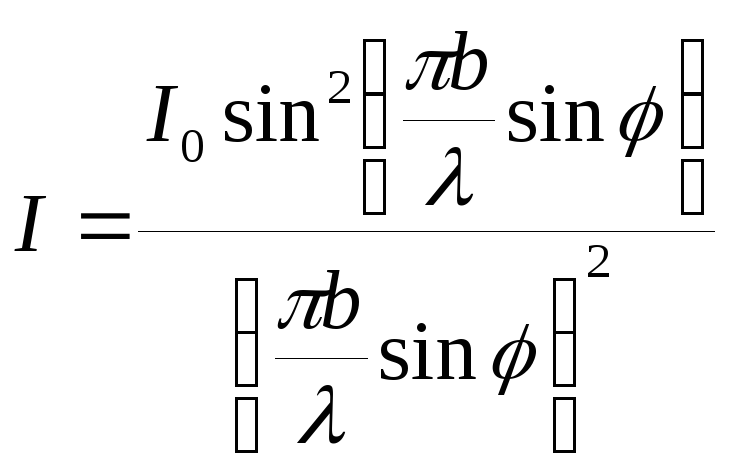 .
Количество минимумов
.
Количество минимумов
![]() (т.к.
(т.к.
![]() ).
Угловая ширина центрального максимума
).
Угловая ширина центрального максимума
![]() .
.
Количественный критерий дифракции Френеля и дифракции Фраунгофера
![]()
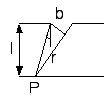 .
Если лучи параллельны, то
.
Если лучи параллельны, то
![]() .
.
![]() .
Если
.
Если
![]() ,
то наблюдается дифракция Фраунгофера
(т.к. порядок l примерно
такой же, как и у r),
если
,
то наблюдается дифракция Фраунгофера
(т.к. порядок l примерно
такой же, как и у r),
если
![]() ,
то наблюдается дифракция Френеля, а
если
,
то наблюдается дифракция Френеля, а
если
![]() ,
то д
,
то д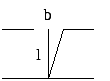 ифракции
нет.
ифракции
нет.
 .
В случае дифракции Фраунгофера в точке
наблюдения на оси системы щель открывает
малую долю первой зоны Френеля.
.
В случае дифракции Фраунгофера в точке
наблюдения на оси системы щель открывает
малую долю первой зоны Френеля.
Многолучевая интерференция
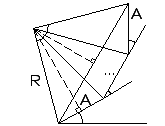
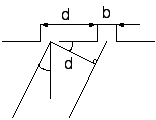
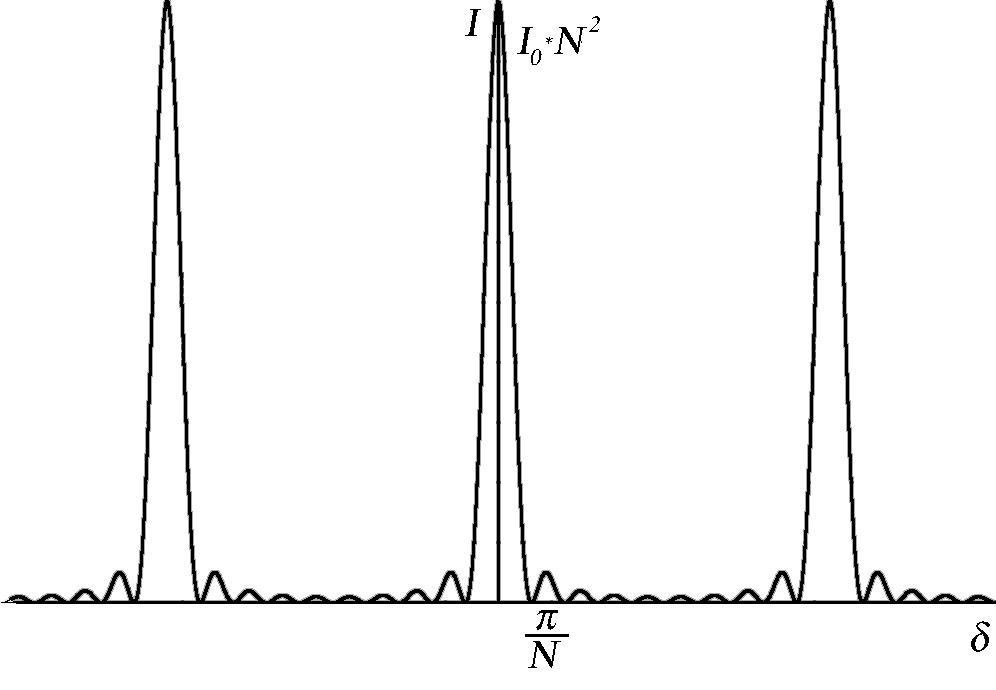
Пусть складывается N
колебаний с одинаковой амплитудой A
и сдвиг фаз между которыми одинаков и
равен . Тогда, как
видно из векторной диаграммы,
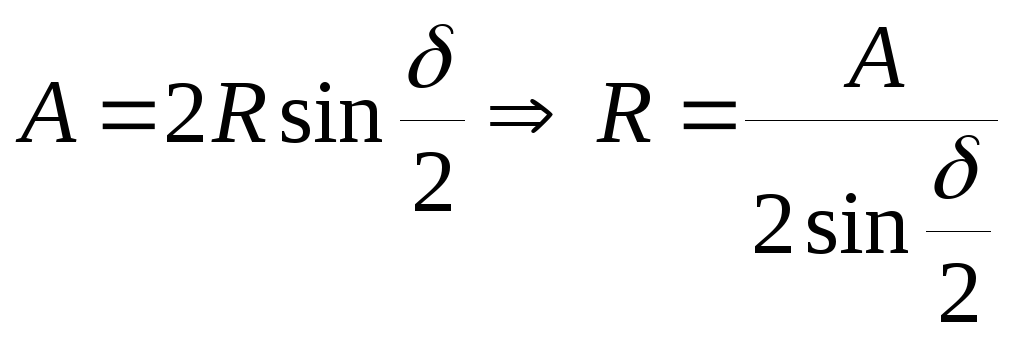 .
Тогда амплитуда суммарного колебания
.
Тогда амплитуда суммарного колебания
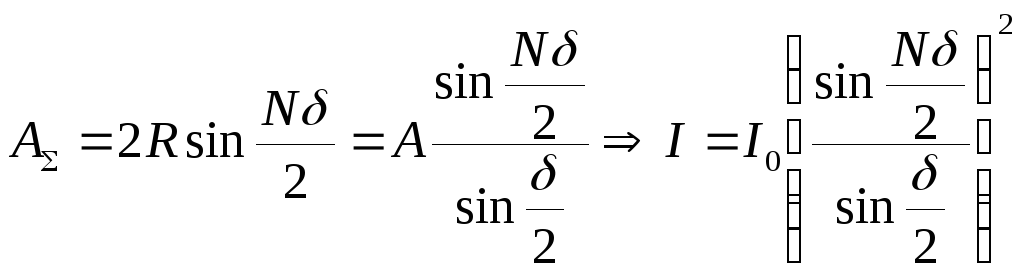 ,
где
,
где
![]() – интенсивность лучей, приходящих в
точку, где складываются колебания. При
– интенсивность лучей, приходящих в
точку, где складываются колебания. При
![]() .
Координаты минимумов:
.
Координаты минимумов:
![]() ,
где k – номер минимума,
,
где k – номер минимума,
![]() .
При
.
При
![]() – резкий максимум.
– резкий максимум.
Дифракционная решётка
Дифракционной решёткой называется система из одинаковых щелей, расположенных на одинаковом расстоянии в линию.
Т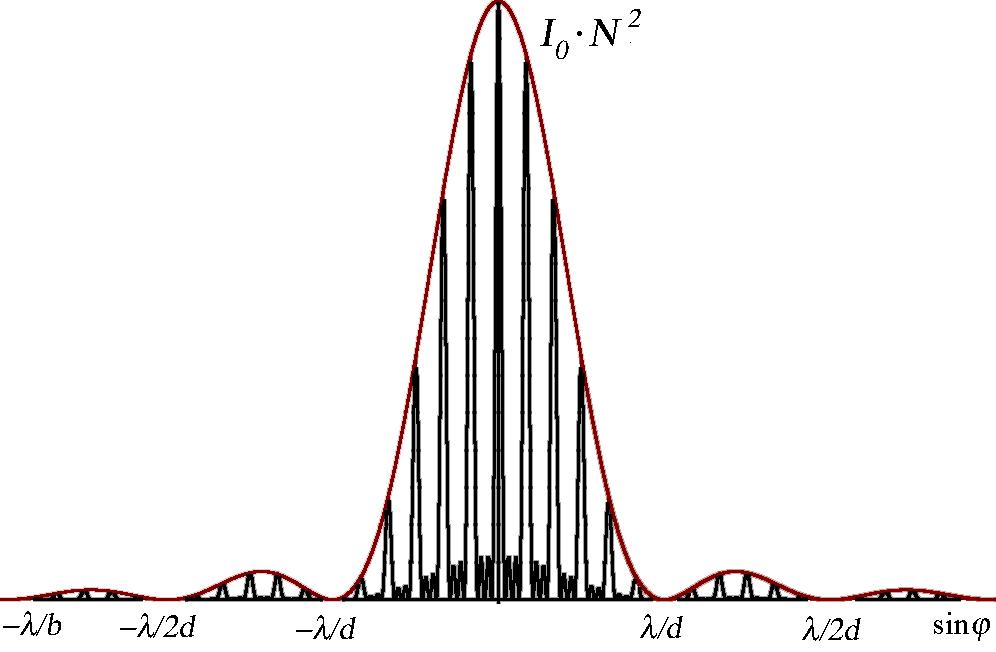 ак
как на щелях дифракционной решётки
происходит дифракция Фраунгофера, то
распределение интенсивности
ак
как на щелях дифракционной решётки
происходит дифракция Фраунгофера, то
распределение интенсивности
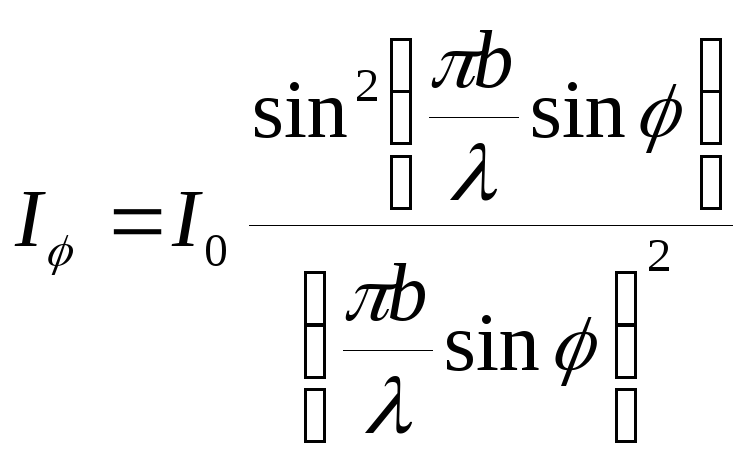 .
.
Оптическая разность хода
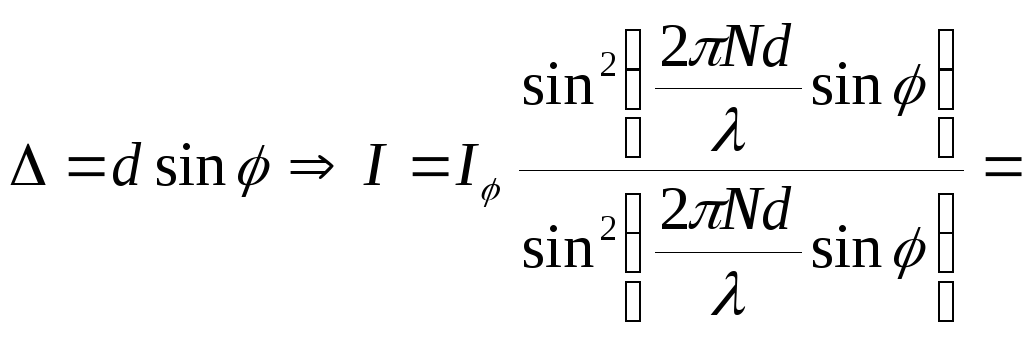
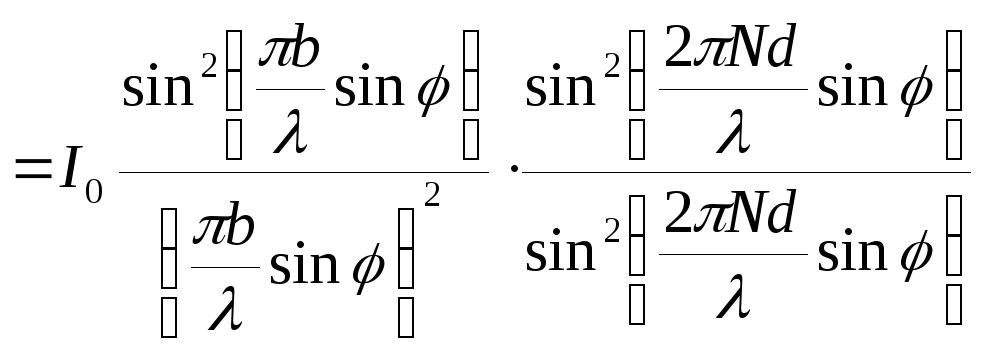 .
.
Условие минимума:
![]() .
Угловая ширина центрального максимума:
.
Угловая ширина центрального максимума:
![]() .
.
Основные характеристики спектрального прибора:
Угловая дисперсия – величина
![]() ,
где
,
где
![]() – разность углов, соответствующих
разным длинами волн,
– разность углов, соответствующих
разным длинами волн,
![]() – разность этих длин волн,
– разность этих длин волн,
![]() при малых
при малых
![]() .
.
Разрешающая сила или
разрешающая способность – величина
![]() .
.
Критерий Релея: Два близких максимума воспринимаются раздельно, если середина одного максимума совпадает с краем другого.
![]() – условие максимума для волны
– условие максимума для волны
![]() ,
,
![]() – условие соседнего минимума для волны
. По критерию
– условие соседнего минимума для волны
. По критерию
![]() .
.
Формула Брэгга-Вульфа:
![]() – условие максимума при дифракции
отражённых рентгеновских лучей на
кристалле.
– условие максимума при дифракции
отражённых рентгеновских лучей на
кристалле.
Дифракция на кристалле используется для анализа спектрального состава рентгеновского излучения и ля исследования кристаллов.
Поляризация
Разложим
![]() на компоненты:
на компоненты:
![]() и пусть
и пусть
![]() .
Тогда
.
Тогда
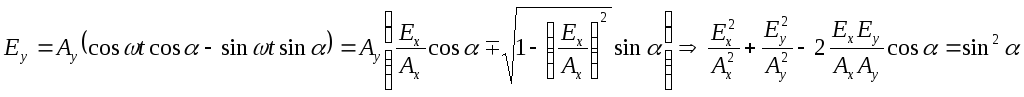 – уравнение траектории конца
– уравнение траектории конца
![]() .
.
При
![]() будет
будет
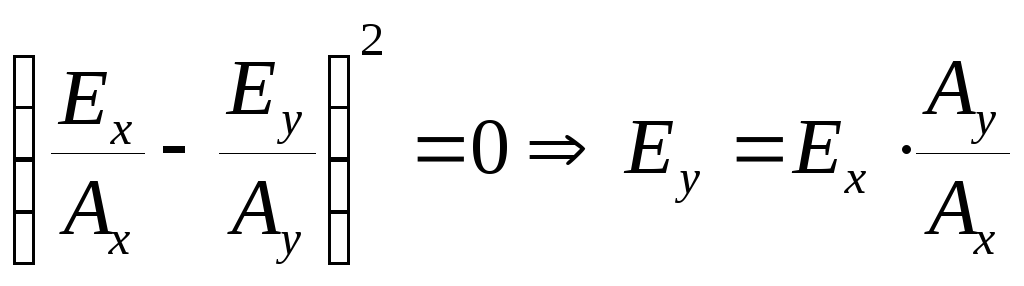 – линейная поляризация.
– линейная поляризация.
При
![]() будет
будет
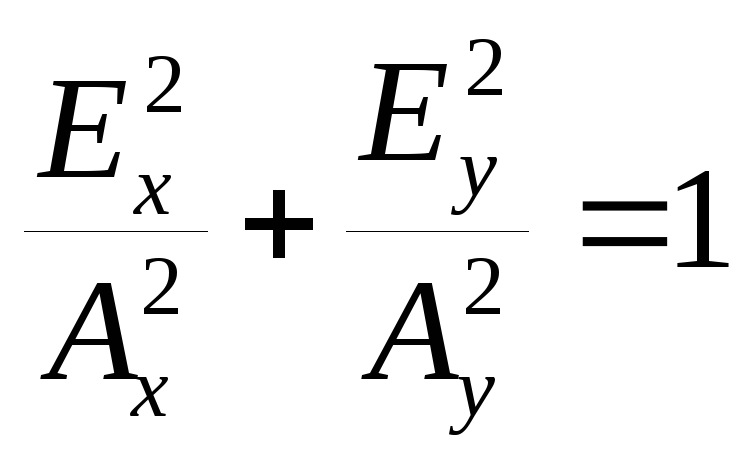 – эллиптическая поляризация. Если
вдобавок
– эллиптическая поляризация. Если
вдобавок
![]() ,
то поляризация круговая.
,
то поляризация круговая.
Поляризатор пропускает все волны,
![]() в которых колеблется в определённом
направлении (например,
в которых колеблется в определённом
направлении (например,
![]() ).
Тогда, если
).
Тогда, если
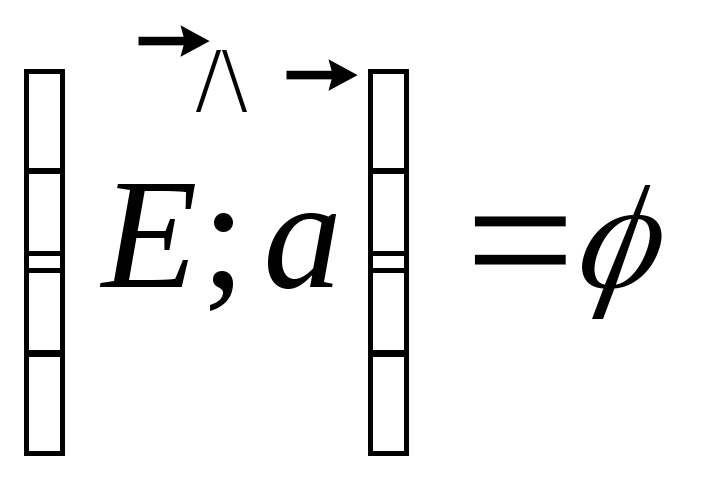 ,
то
,
то
![]() и, т.к.
и, т.к.
![]() ,
,
![]() – закон Моллюса.
– закон Моллюса.
Степень поляризованности
света
![]() .
.
Формулы Френеля
Р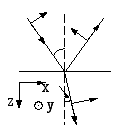 азложим
векторы:
азложим
векторы:
![]() ,
где «||» – вектор, лежащий в плоскости
рисунка и перпендикулярный лучу, «»
– вектор, параллельный оси y.
,
где «||» – вектор, лежащий в плоскости
рисунка и перпендикулярный лучу, «»
– вектор, параллельный оси y.
Условия на границе раздела двух
диэлектриков:
![]() ,
т.е.
,
т.е.
![]() ,
т.к.
,
т.к.
![]() лежит в плоскости xy.
Из рисунка видно, что
лежит в плоскости xy.
Из рисунка видно, что
![]()
![]() .
Обозначим
.
Обозначим
![]() .
Тогда
.
Тогда
![]() ,
,
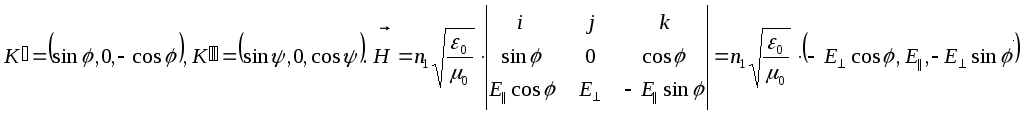
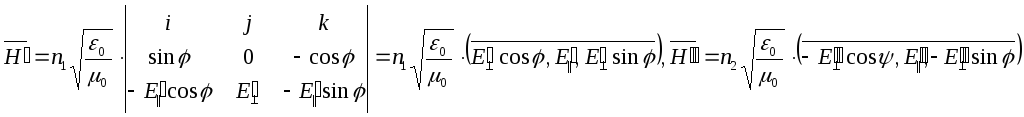 .
.
Таким образом,
![]() .
.
Отсюда следует, что
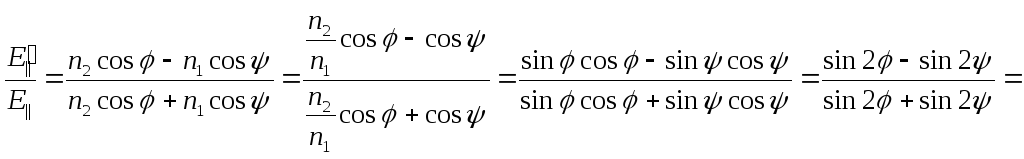
![]() .
Если
.
Если
![]() ,
то в отражённом свете будет отсутствовать
,
то в отражённом свете будет отсутствовать
![]() ,
т.е. свет будет поляризован.
,
т.е. свет будет поляризован.
![]() – соответствующий угол падения (угол
Брюстера).
– соответствующий угол падения (угол
Брюстера).
![]() ,
где
,
где
![]() – закон Брюстера.
– закон Брюстера.
Формулы Френеля:
-
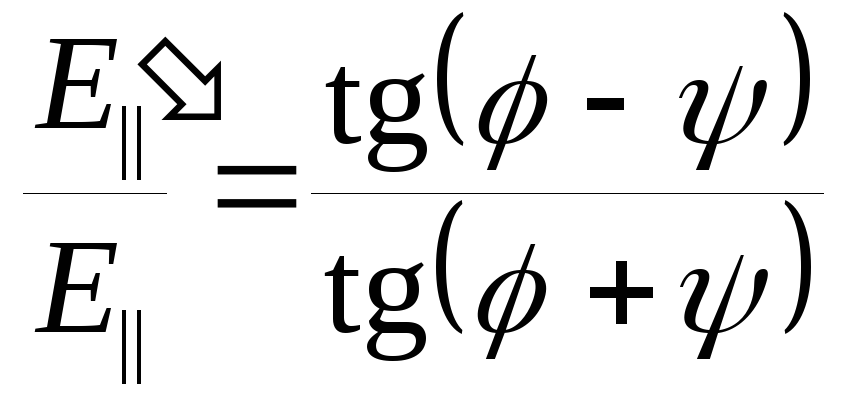 ;
; -
 ;
; -
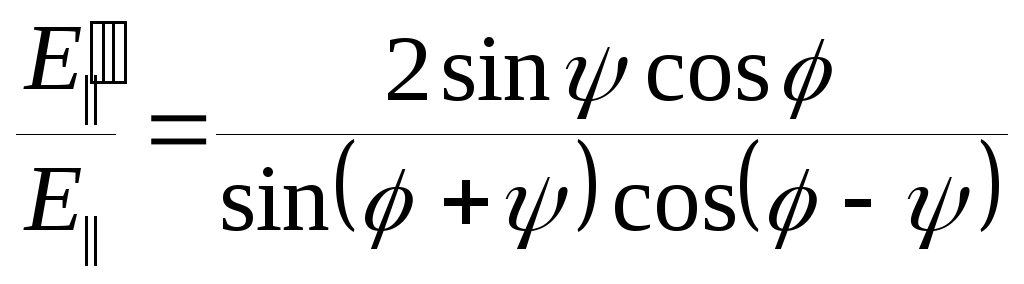 ;
; -
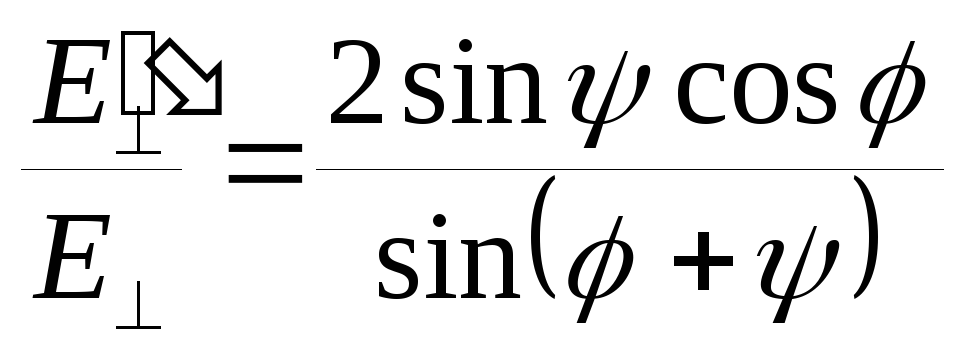 .
.
Рассмотрим случай почти нормального
падения, т.е. когда
и – очень малые
углы. Тогда
![]() и формулы преобразуются следующим
образом:
и формулы преобразуются следующим
образом:
-
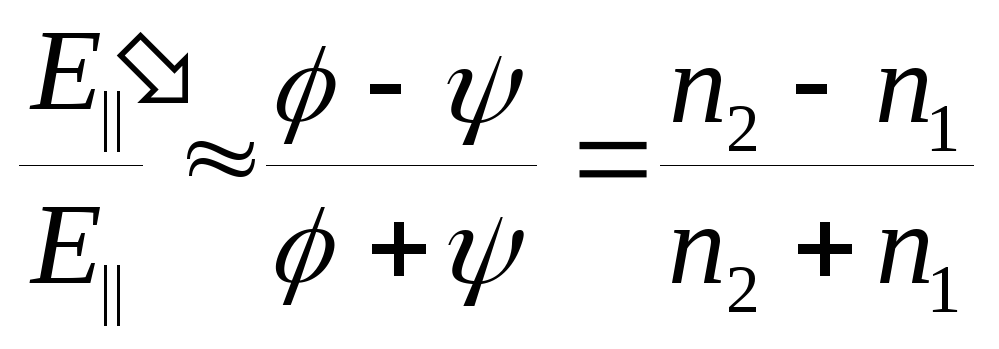 ;
; -
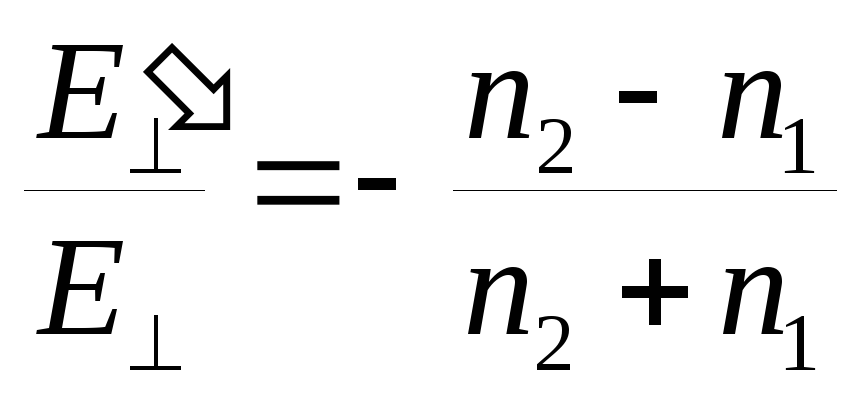 ;
; -
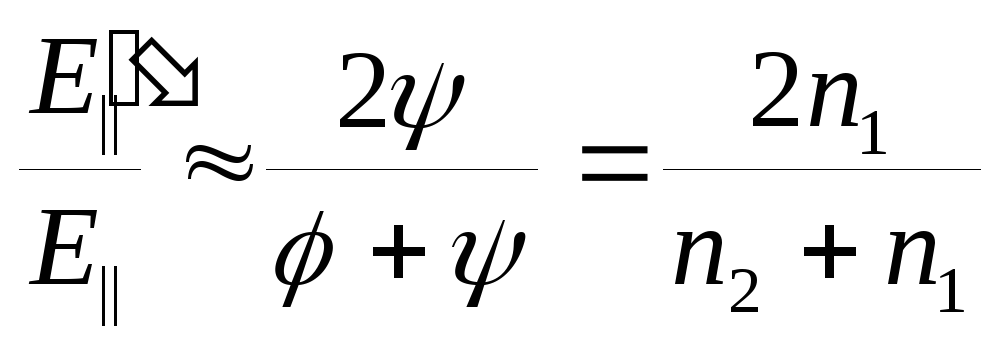 ;
; -
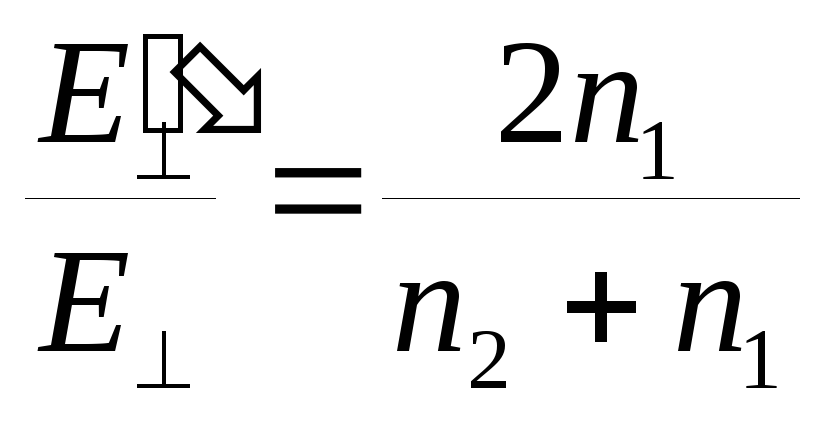 .
.
![]() при
при
![]() ,
следовательно, на рисунке направление
,
следовательно, на рисунке направление
![]() выбрано верно, а, значит, при отражении
от оптически более плотной среды фаза
действительно скачком меняется на .
выбрано верно, а, значит, при отражении
от оптически более плотной среды фаза
действительно скачком меняется на .
Если
![]() ,
то можно подобрать такой угол падения,
что
,
то можно подобрать такой угол падения,
что
![]() ,
т.е.
,
т.е.
![]() .
Тогда
.
Тогда
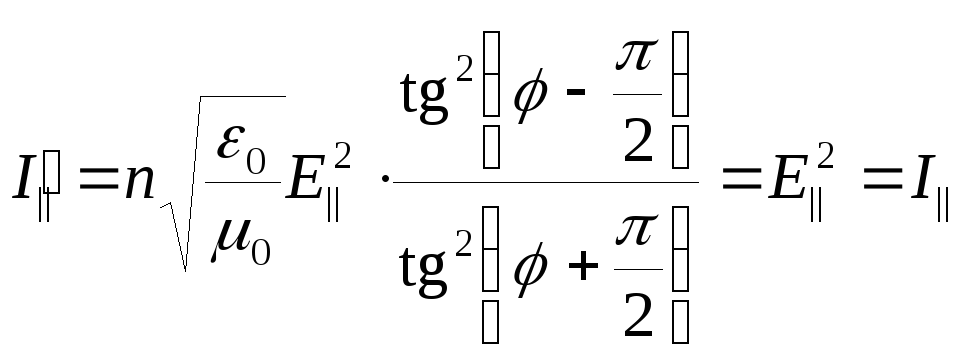 .
Аналогично
.
Аналогично
![]() и
и
![]() ,
следовательно, в среду с оптической
плотностью
,
следовательно, в среду с оптической
плотностью
![]() луч не проходит.
луч не проходит.
Коэффициент отражения
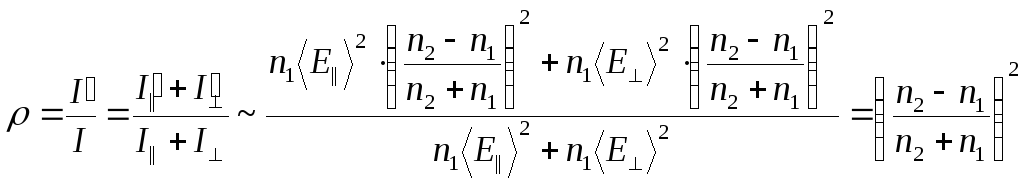 .
.
Коэффициент прохождения
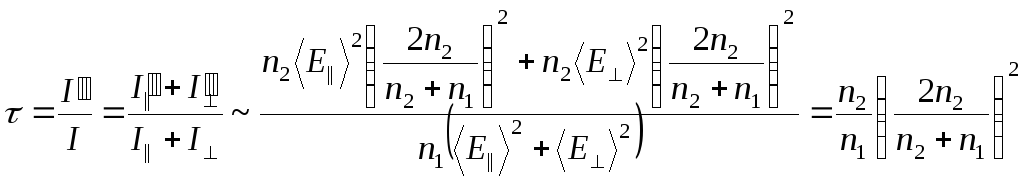 .
.
Двойное лучепреломление
Это явление наблюдается при прохождении света через кристаллы, не обладающие кубической структурой. Явление заключается в том, что луч распадается на два, причём каждый распространяется со своей скоростью и, вообще говоря, в разных направлениях.
Оптическая ось кристалла – направление, при распространении луча света вдоль которого разделение на два луча не происходит.
Любая плоскость, содержащая ось кристалла, называется главным сечением кристалла.
Луч, для которого выполняются законы преломления, называется обыкновенным, другой – необыкновенным.
Оба луча оказываются линейно поляризованными во взаимно перпендикулярных направлениях. Плоскость колебаний обыкновенного луча перпендикулярна плоскости кристалла.
Диаграммы скоростей:
К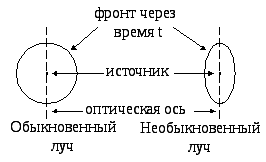 ристаллы,
в которых обыкновенный луч движется
быстрее необыкновенного, называются
положительными, другие – отрицательными.
ристаллы,
в которых обыкновенный луч движется
быстрее необыкновенного, называются
положительными, другие – отрицательными.
Интерференция поляризованных лучей
Пусть есть кристаллическая пластина,
вырезанная вдоль оптической оси и на
неё нормально падает луч света с длиной
волны . Тогда
два луча – обыкновенный и необыкновенный
– будут двигаться с разными скоростями
и, следовательно, для них будут разные
показатели преломления. Обозначим
![]() – оптическая плотность для обыкновенного
луча,
– оптическая плотность для обыкновенного
луча,
![]() – для необыкновенного. Тогда оптическая
разность хода
– для необыкновенного. Тогда оптическая
разность хода
![]() ,
где d – толщина
пластинки. Разность фаз
,
где d – толщина
пластинки. Разность фаз
![]() .
.
Кристаллическая пластинка,
вырезанная вдоль оптической оси с
толщиной
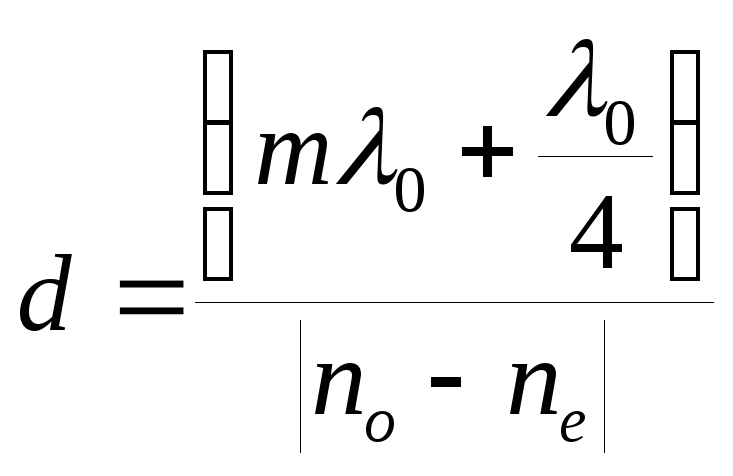 называется пластинкой в четверть длины
волны; с толщиной
называется пластинкой в четверть длины
волны; с толщиной
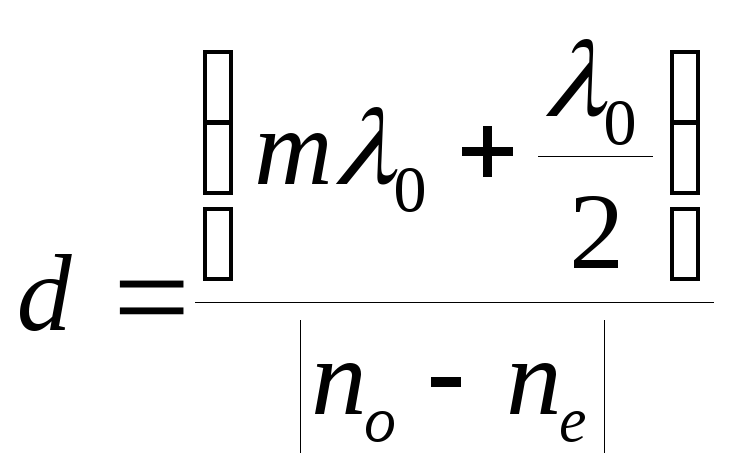 – пластинкой в половину длины волны.
– пластинкой в половину длины волны.
Искусственное двойное лучепреломление
Э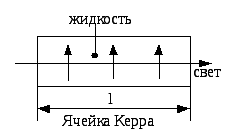 ффект
Керра:
ффект
Керра:
![]() .
Разность фаз обыкновенного и необыкновенного
луча после прохождения такой ячейки
.
Разность фаз обыкновенного и необыкновенного
луча после прохождения такой ячейки
![]() ,
где B – постоянна
Керра.
,
где B – постоянна
Керра.
Явление двойного лучепреломления может возникать и в кристаллах с кубической структурой и в аморфных телах при создании в них механической деформации.
Вращение плоскости поляризации
При прохождении плоскополяризованного
света через оптически активное вещество
плоскость поляризации поворачивается
на угол, пропорциональный длине пути
света в этом веществе:
![]() .
Если это вещество – жидкость, то
.
Если это вещество – жидкость, то
![]() ,
где
,
где
![]() – удельная постоянная вращения, c
– концентрация вещества, растворённого
в жидкости.
– удельная постоянная вращения, c
– концентрация вещества, растворённого
в жидкости.
Дисперсия
Пусть складываются две волны:
![]() .
Разность фаз
.
Разность фаз
![]() .
Приращение разности фаз
.
Приращение разности фаз
![]() .
Перейдём в такую систему отсчёта, что
.
Перейдём в такую систему отсчёта, что
![]() ,
т.е. в систему отсчёта, связанную с
движением «горба» биения. Тогда
,
т.е. в систему отсчёта, связанную с
движением «горба» биения. Тогда
![]() .
.
