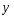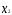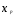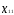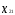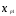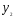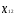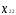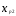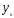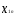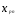Лекция №3
Множественная регрессия. Мультиколлинеарность данных
Множественной регрессией называют уравнение связи с несколькими независимыми переменными:
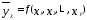 (3.1)
(3.1)
Переменная у называется зависимой,
объясняемой или результативным
признаком.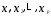 –
независимые, объясняющие переменные
или факторные признаки (факторы).
–
независимые, объясняющие переменные
или факторные признаки (факторы).
Соответствующая регрессионная модель имеет вид
 ,
(3.2)
,
(3.2)
где ε -ошибка модели, являющаяся случайной величиной.
Множественная регрессия применяется в ситуациях, когда из множества факторов, влияющих на результативный признак, нельзя выделить один доминирующий фактор и необходимо учитывать влияние нескольких факторов. Например, объем выпуска продукции определяется величиной основных и оборотных средств, численностью персонала, уровнем менеджмента и т. д., уровень спроса зависит не только от цены, но и от имеющихся у населения денежных средств.
Основная цель множественной регрессии – построить модель с несколькими факторами и определить при этом влияние каждого фактора в отдельности, а также их совместное воздействие на изучаемый показатель.
Постановка задачи множественной
регрессии: по имеющимся данным n
наблюдений (табл. 3.1) за совместным
изменениемp+1 параметраy и
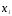 и
((
и
((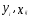 );i=1, 2, ...,n;j=1, 2,
…,p) необходимо определить
аналитическую зависимость
);i=1, 2, ...,n;j=1, 2,
…,p) необходимо определить
аналитическую зависимость ,
наилучшим образом описывающую данные
наблюдений.
,
наилучшим образом описывающую данные
наблюдений.
Таблица 3.1
Результаты наблюдений
|
|
|
|
|
… |
|
|
1 |
|
|
|
… |
|
|
2 |
|
|
|
… |
|
|
… |
… |
… |
… |
… |
… |
|
n |
|
|
|
… |
|
Каждая строка таблицы содержит p +1
число и представляет собой результат
одного наблюдения. Наблюдения различаются
условиями их проведения. Вопрос о том,
какую зависимость следует считать
наилучшей, решается на основе какого-либо
критерия. В качестве такого критерия
обычно используется минимум суммы
квадратов отклонений расчетных или
модельных значений результативного
показателя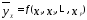 от наблюдаемых значений
от наблюдаемых значений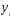
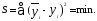
Построение уравнения множественной регрессии предполагает решение двух задач:
1) спецификация модели;
2) оценка параметров выбранной модели.
В свою очередь, и спецификация модели включает в себя решение двух задач:
– отбор p факторовxj, подлежащих включению в модель;
– выбор вида аналитической зависимости
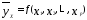 .
.
Для измерения степени тесноты связи между изменениями величины результативного признака (у) и изменениями значений факторных признаков определяется коэффициент множественной (совокупной) корреляции (R). Для случая зависимости результативного признака от двух факторных признаков формула совокупного коэффициента корреляции имеет вид:
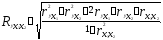 (3.3)
(3.3)
Если число факторов-признаков более двух, то совокупный
коэффициент корреляции определяется следующим образом:
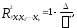 (3.4)
(3.4)
где
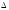 — матрица парных коэффициентов корреляции
(см. табл. 3.1);
— матрица парных коэффициентов корреляции
(см. табл. 3.1);
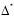 —соответствует
матрице парных коэффициентов корреляции
(
—соответствует
матрице парных коэффициентов корреляции
(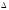 )
без верхней строки и первого столбца.
)
без верхней строки и первого столбца.
Величина
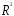 называется коэффициентом детерминации,
она показывает, в какой мере вариация
результативного признака обусловлена
влиянием признаков-факторов, включенных
в уравнение множественной зависимости.
называется коэффициентом детерминации,
она показывает, в какой мере вариация
результативного признака обусловлена
влиянием признаков-факторов, включенных
в уравнение множественной зависимости.
Величина совокупного
коэффициента корреляции
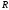 изменяется
в пределах от 0 до 1 и численно не может
быть меньше, чем любой из образующих
его парных коэффициентов корреляции.
Чем ближе он к единице, тем меньше роль
неучтенных в модели факторов и тем более
оснований считать, что параметры
регрессионной модели отражают степень
эффективности включенных в нее факторов.
изменяется
в пределах от 0 до 1 и численно не может
быть меньше, чем любой из образующих
его парных коэффициентов корреляции.
Чем ближе он к единице, тем меньше роль
неучтенных в модели факторов и тем более
оснований считать, что параметры
регрессионной модели отражают степень
эффективности включенных в нее факторов.
Для оценки существенности (значимости) совокупного коэффициента корреляции используется критерий F-Фишера.
Для этого по
формуле (7.43) определяется F-расчетное,
которое сравнивается с табличным
значением при
заданном уровне значимости
 (например,
(например,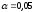 ).
Если
).
Если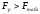 ,то с вероятностью
0,95 можно утверждать, что связь между
результативным и факторными признаками
существенна.
,то с вероятностью
0,95 можно утверждать, что связь между
результативным и факторными признаками
существенна.