1) Синхронный двигатель сд работает без арв

Схема замещения представлена на рис.5.

Сопротивление двигателя Х_d* = 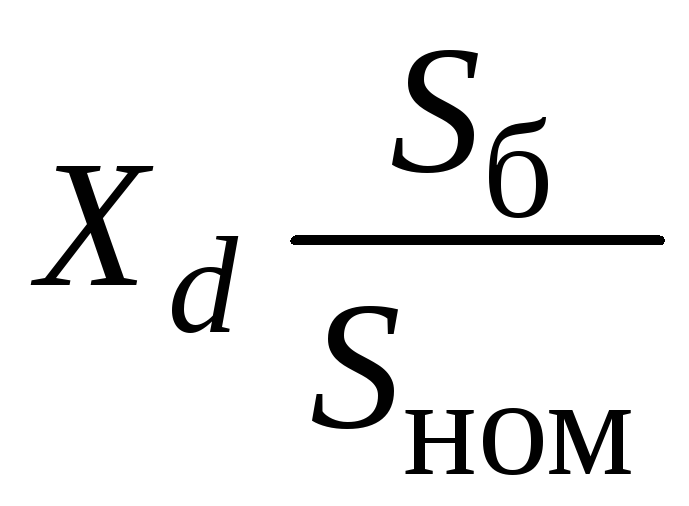= 1,9.

Передаваемая мощность Р₀ = Р_нК_з/S_б = 1860∙32∙0,85/64,7 = 0,78; напряжение на шинах - U_н = 1; реактивная мощность СД Q₀ = Р₀ tgφ = 0,78∙0,43 = 0,34.

ЭДС синхронного двигателя

.

Максимальная мощность

Р_макс = UЕ_q/Х_d = 1∙2,22/1,9 = 1,19

Коэффициент запаса по мощности

= (1,19 – 0,78)/0,78 = 0,53 (53 %)

Критическое напряжение U_кр = Р₀Х_d/E_q = 0,78∙1,9/2,22 = 0,67

Коэффициент запаса СД по напряжению

= 0,33 ( или 33 %)

2) Синхронный двигатель сд работает с арв пропорционального действия

Параметры схемы замещения равны (рис. 6).

Cвехпереходное сопротивление = = 0,2.

Сверхпереходная ЭДС синхронного двигателя

1,08

Критическое напряжение U_кр = Р₀/ = 0,78∙0,2/1,08 = 0,14.

Коэффициент запаса СД по напряжению

= = (1- 0,14)/1 = 0,86 (86 %).

Вывод: коэффициент запаса статической устойчивости СД с АРВ больше, чем СД без АРВ

б) синхронная ЭДС Е_qэ эквивалентного генератора Г постоянна

Параметры схемы замещения равны (рис.7):

Трансформаторов Т1 и Т2

Х_т1 = Х_т2 == (10,5∙64,7)/(100∙40) = 0,17

Генератора Г

Х_dГ = = 1,6∙64,7/75 = 1,38

Линии Л

Х_лэ == 0,5∙0,4∙50∙64,7/115²= 0,05.

Суммарное сопротивление

Х_dΣ = Х_dГ + Х_т1 + Х_т2 + Х_лэ = 1,38 + 0,049 + 0,17 + 0,17 = 1,77

ЭДС генератора

ЭДС синхронного двигателя

.

Максимальная мощность

Р_макс = Е_qГЕ_q/(Х_d∑ + Х_d) = 2,115∙1,52/(1,77 + 1,9) = 0,876

Коэффициент запаса по мощности

К^Р_з = = (0,877 – 0,78)/0,78 = 0,123 (12,3 %)

Критическая ЭДС генератора

Е_кр = Р₀(Х_dΣ + Х_d)/E_q = 0,78(1,77 + 1,9)/1,52 = 1,88.

Коэффициент запаса сд по эдс

= (2,12 – 1,88)/2,12 = 0,112 (11,2 %)

Вывод: Запас статической устойчивости эквивалентного синхронного двигателя СД значительно меньше, чем одиночного двигателя, работающего на шины постоянного напряжения..

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 12

Наброс нагрузки на синхронный двигатель

Исходные данные: активная мощность синхронного двигателя СД в системе относительных единиц Р₀ = 0,77; напряжение U_н = 1; реактивная мощность СД Q₀ = 0,48; переходное сопротивление двигателя СД = 0,2.

Определить методом площадей максимальный угол δ_макс нерегулируемого СД при увеличении механической нагрузки от Р_мех1 = 1 до Р_мех2 = 1,5. Если динамическая устойчивость СД при этом нарушится, то определить угол δ_отк, при котором необходимо снизить механическую нагрузку до Р_мех1 = 1 для сохранения динамической устойчивости. Для определения углов δ_макс и δ_отк построить зависимость активной мощности от угла δ при неизменном напряжении на шинах СД.

Решение.

Переходная ЭДС синхронного двигателя

1,08.

Выражение мощности СД

Р = =(U/)sinδ = 1·1,077/0,2sinδ = 5,4sinδ.

Начальный угол

= arctg(P₀/+Q₀) =arctg(0,77∙0,2/1 + 0,48∙0,2) = 8º.

На рис. 1. изображена зависимость мощности двигателя от угла P = f(δ)

Р, о.е.

5,4

d

1,11 а Р_мех2

0,77 с е

в Р_мех1

8 24 172 δ, град

Рис.1. Наброс нагрузки на синхронный двигатель

Площадка ускорения F_уск = F_abc; площадка торможения F_торм = F_cde.

Начальный механический момент М₀ = Р_мех1 = 0,77.

Максимальный момент = U/= 5,4.

Момент при увеличении нагрузки М_мех2 = Р_мех2 = 1,5.

Критический угол

_кр = 180 - arcsinМ₀/ = 180 – arcsin0,77/5,4 = 180 – 8,2 = 171,8

Наброс нагрузки на СД может продолжаться сколь угодно долго, т.к.площадка ускорения значительно меньше, чем площадка торможения. Размах колебаний угла составляет _макс = 24 .

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 13

ТЕМА. ИССЛЕДОВАНИЕ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ

ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОГО УГЛА ОТКЛЮЧЕНИЯ.

Пример 6.

Найти предельный угол отключения короткого замыкания _от.пр в случае, когда на линии Л в точке К возникло трехфазное короткое замыкание (рис. 1). При определении предельного времени отключения t_пр не учитывать электромагнитные переходные процессы в обмотке возбуждения генератора и действия АРВ.

Г Т К Л U_с

Рис. 1. Исследуемая система

Исходные данные:

Генератор Г: S_н = 250 МВА, U_н = 10,5 кВ, cos = 0,8, Х_d1 = 1,8; = 0,28,Х_2г = 0,23, постоянная инерции Т_jг = 11 с, постоянная обмотки возбуждения Т_d0 = 6,5 с, постоянная времени регулятора Т_e = 1 с.

Трансформатор Т: S_н1 = 250 МВА, U_вн = 220 кВ, U_нн = 10,5 кВ, напряжение КЗ U_к = 11 %.

Линия Л: длина l = 240 км, сопротивление прямой последовательности Х₁ = 0,43 Ом/км, нулевой последовательности Х₀ = 3Х₁, напряжение системы U_с = 230 кВ.

Режим: передаваемая мощность P₀ = 200 МВт, cos = 0,85.

Решение.

Расчеты элементов проводим в системе относительных единиц. Примем S_б = 1000 МВА и базисные напряжения равными средним номинальным U_ср.ном. Сопротивления элементов схемы замещения (рис. 2):

Генератора: = 0,28= 1,12;Х_d* = 1,8= 7,2;

Х_2* = 0,23= 0,92;

Трансформатора Т: Х_т1 = = 0,44;

Линии Л: прямой последовательности Х_л = 0,43240= 2,04;

нулевой - Х_л0 = 32,04 = 6,12.

Постоянная инерции Т_j = Т_jг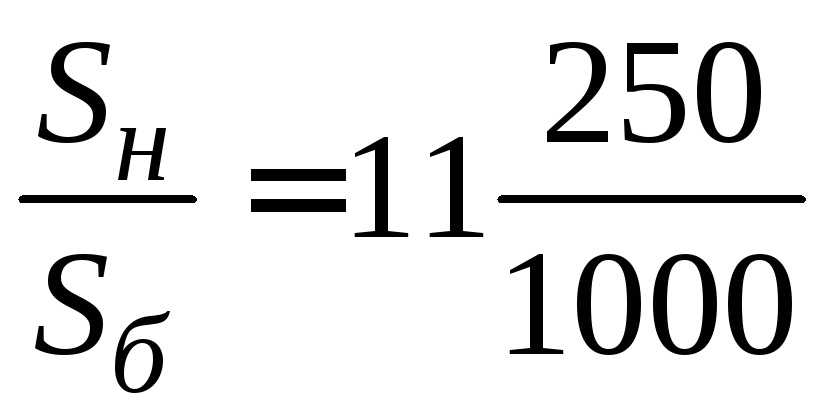 = 2,75 с.

Передаваемая мощность: P_0* = = 0,2

Реактивная Q_0* = = 0,124

где Q₀ = P₀tg₀ = 2000,62 = 124 Мвар.

Напряжение системы U_c* = U_c/U_cр.ном = 230/230 = 1.

Собственная реактивность системы для нормального режима (рис. 2)

= = + X_т + 0,5Х_л = 1,12 + 0,44 + 1,07 = 2,63;

X_d = X_d + X_т + 0,5Х_л = 7,2 + 0,44 + 1,07 = 8,71.

Собственная проводимость системы для нормального режима

= 1/ = 1/2,63 = 0,38.

Взаимная проводимость = = 0,38.

Переходная ЭДС генератора

= .

Начальный угол

 = arctg.

Угол между векторами Е_q* и U_с*:

₀ = arctg.

Переходная ЭДС = cos(₀ - ) =1,43cos(41,2˚ – 21,61˚) = 1,35.

Предел передаваемой мощности в нормальном режиме

= U_с* = 1,3510,38 = 0,51.

Рассмотрим послеаварийный режим системы, когда одна линия отключена (рис. 3).

Собственная реактивность системы для послеаварийного режима

= + X_т + Х_л = 1,12 + 0,44 + 2,14 = 3,7.

Собственная проводимость = 1/ = 1/3,7 = 0,27.

Взаимная проводимость = = 0,27; = 0˚.

Предел передаваемой мощности в послеаварийном режиме режиме

P^II_m = Е_qU_с*Y^II₁₂ = 1,3510,27 = 0,36.

Рассмотрим аварийный режим – режим КЗ (рис. 4).

Дополнительное сопротивление X⁽³⁾ = 0.

Предел передаваемой мощности в аварийном режиме = 0, подставим значение этой мощности в формулу предельного угла отключения. Получим

cos_от.пр ==

=,

Предельный угол отключения составит _от.пр = arccos0,298 = 72,7.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3

ТЕМА. ВЛИЯНИЕ ПАРАМЕТРОВ ЭЛЕМЕНТОВ СИСТЕМЫ

Пример 4.

На рис. 1 показана электрическая система, состоящая из источника бесконечной мощности, представленной шинами постоянного напряжения с U_с = 230 кВ , станции С, состоящий из двух генераторов, трансформатора Т, линии Л.

С Т Л U_с

Р₀

Рис. 1. Исследуемая система

Исходные данные:

Генераторы станции С: S_н = 125 МВА, n = 2 шт.; U_н = 10,5 кВ, cos = 0,8, Х_d(н) = 1,91; = 0,28.

Трансформатор Т: S_н = 250 МВА, К_т = 220/10,5 кВ; U_к = 11 %.

Линия Л: длина l = 240 км, Х₀ = 0,43 Ом/км, U_вн = 220 кВ.

Передаваемая мощность P₀ = 200 мВт, cos = 0,85.

Требуется исследовать влияние на статическую устойчивость системы переходного сопротивления генераторов и длины линии. Построить зависимости коэффициента запаса в функции от переходного сопротивления К_з = () и коэффициента запаса в функции от длины линии К_з = (l).

Решение.

Расчеты элементов проводим в системе относительных единиц при приближенном приведении. Примем S_б = 125 МВА и базисные напряжения равными средним номинальным напряжениям U_ср.ном. Сопротивления элементов схемы замещения системы:

Трансформатора Т: Х_т1 = Х_т2 = = = 0,055.

Генераторов Г: .

= = 0,50,28= 0,14.

Линии Л: Х_л = 0,5Хl = 0,50,43240= 0,13.

Передаваемые мощности:P_0* = = 1,6;

Q_0* = = 0,99,гдеQ₀ = P₀tg₀ = 2000,62 = 123,95 Мвар.

Напряжение системы U_c* = U_c/U_cр.ном = 230/230 = 1.

Переходная ЭДС: ,

где =+ Х_т1* + Х_т2* + Х_лэ* = 0,14 + 0,055 + 0,133 = 0,328.

Начальный угол между векторами Е_q и U_с

₀ = arctg.

где X_d* = Х_d* + Х_т1* + Х_т2* + Х_лэ* = 0,955 + 0,055 + 0,133 = 1,14.

Угол между векторами и U_с

= arctg arctg .

Поперечная составляющая переходной ЭДС

= Есos(₀ - ) = 1,42cos(40,63 – 21,61) = 1,34.

Уравнение мощности генератора с АРВ пропорционального действия:

=-=

= - = 4,09sin - 1,09sin2.

= 4,087сos - 21,085сos2 = 4,085сos - 2,174сos2 =

= 4,085сos - 2,174(2сos² - 1) = 4,085сos - 4,348сos² + 2,174 = 0,

или 4,348сos² - 4,085сos - 2,174 = 0 или сos² - 0,94сos - 0,5 = 0.

Решим квадратное уравнение относительно сos и получим

сos₁ = 1,319; сos₂ = - 0,379; _m = 112,27.

Подставим значение _m = 112,27 в уравнение мощности

P_пр = 4,085sin112,27 - 1,087sin2112,27 = 4,543.

Коэффициент запаса статической устойчивости

К_з =

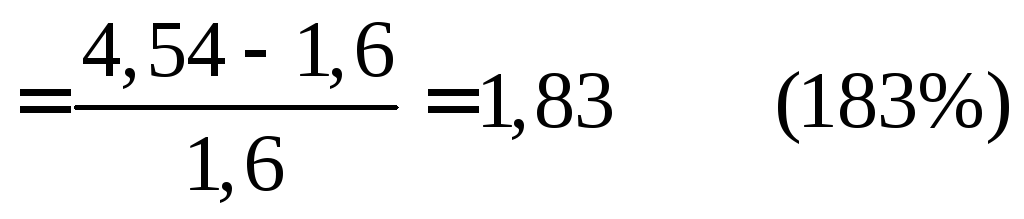
Рассмотрим влияние переходного сопротивления генераторов и длины линии на величину коэффициента запаса статической устойчивости.

Будем задаваться различными значениями переходного сопротивления и длины линии и рассчитывать коэффициент запаса. Результаты расчета представлены в табл.1, 2 и на рис. 2 и 3, по ним построены зависимости коэффициента запаса К_з = () и К_з = (l).

Таблица 1

Результаты расчета коэффициента запаса статической устойчивости системы в зависимости от переходного сопротивления

, о.е.	, о.е.	, о.е.	, град	, о.е.	m, град	Pпр, о.е.	Кз, %
0,12	0,308	1,39	20,69	1,31	112,89	4,77	198,1
0,14	0,328	1,42	21,61	1,34	112,27	4,543	183,9
0,16	0,348	1,46	22,5	1,39	111,48	4,4	175

Таблица 2

Результаты расчета коэффициента запаса статической устойчивости системы в зависимости от длины линии

l, км	Xd, о.е.	, о.е.	0, град	, о.е.	, град	, о.е.	m, град	Pпр, о.е.	Кз, %
200	1,12	0,306	40,36	1,39	20,59	1,31	112,84	4,795	199,7
240	1,143	0,328	40,63	1,42	21,61	1,34	112,27	4,543	183,9
280	1,165	0,35	40,88	1,46	22,58	1,39	111,56	4,377	173,6

К_з, %.

190

180

170

0,1 0,12 0,14 0,16 0,18

Рис. 2. Зависимость К_з = ()

К_з, %.

200

190

180

170

160 200 240 280 300 l, км

Рис. 3. Зависимость К_з = (l)

Выводы:

1. При увеличении переходного сопротивления генератора коэффициент запаса статической устойчивости уменьшается.

2. При увеличении длины линии коэффициент запаса статической устойчивости уменьшается.