50

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО КУРСУ

«ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ»

(7 семестр)

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1

ТЕМА. ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ И ВЗАИМНЫХ ПРОВОДИМОСТЕЙ

Пример 1.

Определить собственные и взаимные проводимости станций системы (рис.1), состоящей из двух станций С1 и С2, работающих на общую нагрузку Н. Нагрузку Н представить постоянным сопротивлением Z_н.

Исходные данные:

Генератор Г1 станции С1: S_н1 = 125 МВА, U_н1 = 10,5 кВ, cos = 0,91, = 0,2; генератор Г2 станции С2: S_н2 = 65 МВА, U_н2 = 10,5 кВ, cos = 0,8, = 0,2.

Трансформаторы Т1: S_н1 = 125 МВА, К_т = 110/10,5, U_к = 10,5 %, Т2: S_н2 = 80 МВА, К_т = 110/10,5, U_к = 10,5 %.

Линия Л: l = 110 км, Х₀ = 0,4 Ом/км, U_н = 110 кВ.

Режим: передаваемая мощность P₀ = 50 МВт, cos = 0,9.

Нагрузка: P_н = 50 МВт, cos = 0,87, напряжение U_c = 115 кВ.

С1 Т1 Л U_c Т2 С2

Р₀ Р₂

Н Р_н

Рис.1. Исследуемая система

Решение.

Расчеты проводим в системе относительных единиц при приближенном приведении. Примем S_б = 1000 МВА и базисные напряжения равными средним номинальным U_ср.ном.

Сопротивления элементов схемы замещения (рис. 2):

Трансформаторов: Х_т1 = = 0,84; Х_т2 = = 1,31.

Генераторов станций С1 и С2 соответственно:

= 0,2= 1,6; = 0,25= 3,8.

Линии Л: Х_л = 0,50,4110= 1,65.

Передаваемая станцией С1 мощность P_01* = = 0,05.

Реактивная Q_01* = = 0,027,

где Q₀₁ = P₀₁tg₀₁ = 500,54 = 27 Мвар.

Напряжение системы: U_c* = U_c/U_cр.ном = 115/115 = 1.

Мощность нагрузки: P_н* = = 0,07;Q_н* == 0,04, гдеQ_н = P_нtg₀ = 700,57 = 39,9 Мвар;

Полная мощность S_н = = 80,57 мВА;

S_н* = = 0,081.

Сопротивление нагрузки: Z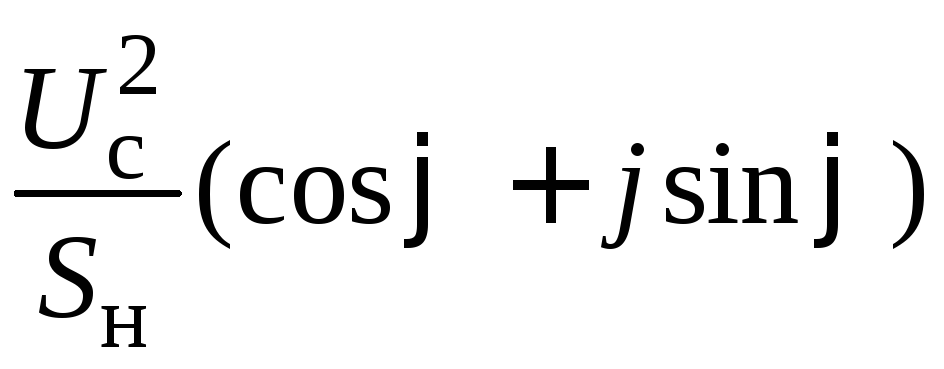_н ==R_н + jX_н =

= 1(cos29,68 + sin29,68) = 10,73 + j6,11.

X_т1 X_л/2 U_c Х_т2

Р₀ Р₂

Р_н Х_н

R_н

Рис. 2. Схема замещения исследуемой системы

Для определения собственной проводимости станции С1 составим схему замещения (рис. 3), приравняв ЭДС станции С2 нулю и преобразуем её к виду, показанному на рис. 4.

Собственное сопротивление станции С1

Z₁₁ = R₁₁ + jX₁₁ = j+ j( R_н + jX_н)/(R_н + jX_н + j) =

= j4,09 + j5,11(10,73 + j6,11)/( j5,11 + 10,73 + j6,11) = 8,03.

где ₁₁ = arctgX₁₁/R₁₁ = arctg7,95/1,14 = 81,84 - угол сдвига цепи нагрузки.

Дополнительный угол ₁₁ = 90 - ₁₁ = 90 - 81,84 = 8,16.

Модуль собственной проводимости Y₁₁ = 1/Z₁₁ = 1/8,03 = 0,12.

Для определения взаимной проводимости станций С1 и С2 заменим “звезду” с сопротивлениями X_1, X_2, Z_н (рис. 3) эквивалентным “треугольником” с сопротивлениями Z₁₂, Z₁₃, Z₂₃ (рис. 4).

Взаимное сопротивление станций С1 и С2

Z₁₂ = R₁₂ + jX₁₂ = j+ j + =j4,09 + j5,11 +

= j9,2 - 20,9/(10,73 + j6,11) = j9,2 + j0,81 - 1,43 = j10,01 - 1,43 = 10,12е^j81,87,

где угол сдига цепи нагрузки ₁₂ = arctgX₁₂/R₁₂ = arctg10,01/1,43 = 81,87.

Дополнительный угол ₁₂ = 90 - ₁₂ = 90 - 81,87 = 8,13.

Модуль взаимной проводимости Y₁₂ = 1/Z₁₂ = 1/10,12 = 0,1.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2

ТЕМА. ИССЛЕДОВАНИЕ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ ПРОСТЕЙШЕЙ НЕРЕГУЛИРУЕМОЙ ЭЛЕКТРИЧЕСКОЙ СИСТЕМЫ

Пример 2.

На рис. 2 показана исследуемая система, состоящая из источника бесконечной мощности, представленной шинами постоянного напряжения с U_с = 340 кВ; генератора Г, двух трансформаторов Т1, Т2 и линии Л.

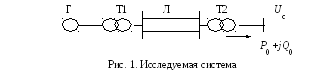
Исходные данные:

Генератор Г: S_н = 125 МВА, U_н = 13,8 кВ, cos = 0,91, Х_d = 1,8, = 0,25.

Трансформатор Т1: S_н = 125 МВА, U_вн = 110 кВ, U_нн = 13,8 кВ, U_к = 10,5 %.

Трансформатор Т2: S_н = 125 МВА, U_вн = 330 кВ, U_нн = 110 кВ, U_к = 10,5 %.

Линия Л: длина l = 120 км, Х₀ = 0,4 Ом/км, U_вн = 110 кВ.

Режим: передаваемая мощность P₀ = 50 мВт, cos = 0,88.

Требуется определить коэффициент запаса статической устойчивости системы для трех случаев: а) генератор не имеет АРВ; б) генератор имеет АРВ пропорционального действия; в) генератор имеет АРВ сильного действия.

Решение.

На рис. 2 приведена схема замещения исследуемой системы. Расчет проводим в системе относительных единиц при приближенном приведении. Примем S_б = 1000 МВА, U_б = U_ср.ном.

Сопротивления элементов исследуемой системы:

трансформаторов Т1 и Т2:

Х_т1 = Х_т2 == = 0,84.

Генератора Г: = = 1,8= 14,4;

= = 0,2= 1,6.

Линии Л: Х_л = 0,5Хl = 0,50,4120= 1,81.

Передаваемая мощность: активная P_0* = 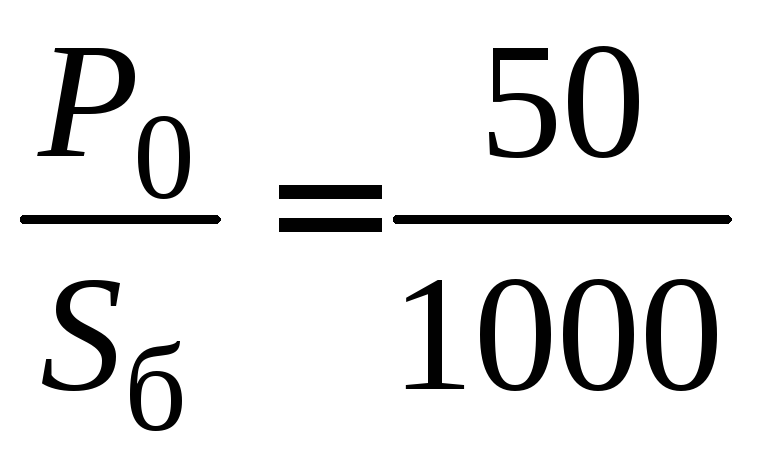= 0,05.

Реактивная Q_0* = = 0,027.

где Q₀ = P₀tg₀ = 500,54 = 27 Мвар.

Напряжение системы U_c* = U_c /U_cр.ном = 340/340 = 1.

а) генератор не имеет АРВ

Предел передаваемой мощности определяется исходя из условия постоянства синхронной ЭДС генератора Е_q* = пост.

Синхронная ЭДС генератора:

где X_d* = Х_d* + Х_т1* + Х_т2* + Х_лэ* = 14,4 + 0,84 + 0,84 +1,81 = 17,89.

Идеальный предел мощности P_пр = .

Коэффициент запаса статической устойчивости системы

К_з =

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3

ТЕМА. ИССЛЕДОВАНИЕ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ ПРОСТЕЙШЕЙ РЕГУЛИРУЕМОЙ ЭЛЕКТРИЧЕСКОЙ СИСТЕМЫ

Пример 3. Требуется исследовать влияние АРВ на статическую устойчивость системы для примера 2.

Решение.

а) генератор имеет АРВ пропорционального действия (ПД)

Предел передаваемой мощности определяется исходя из условия постоянства переходной ЭДС генератора = пост.

Переходная ЭДС генератора:

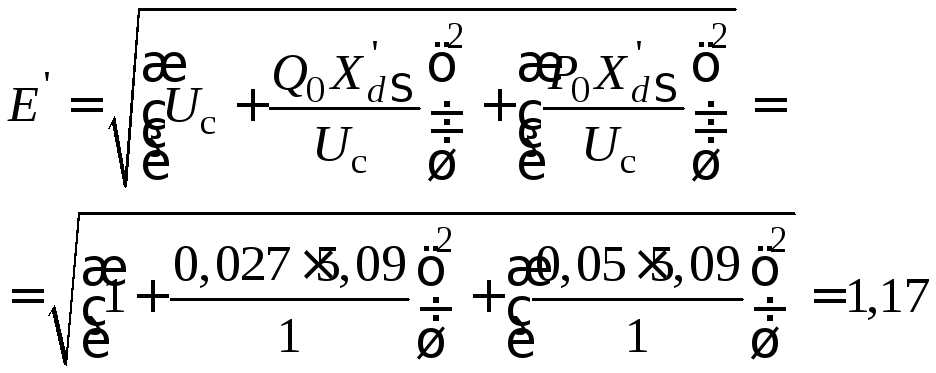
где =+ Х_т1* + Х_т2* + Х_лэ* = 1,6 + 0,84 + 0,84 +1,81 = 5,09.

Угол между векторами иU_с* :

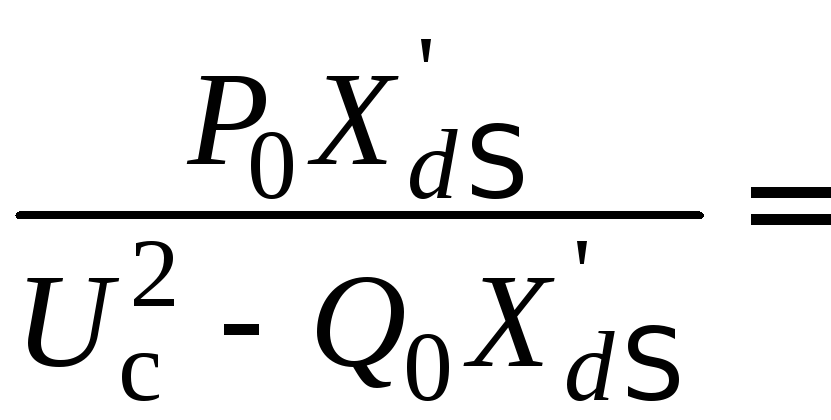= arctg arctg .

Угол между векторами Е_q* и U_с*:

₀ = arctg= arctg.

Переходная ЭДС по поперечной оси

= Есos(₀ - ) = 1,17сos(31,22˚ – 16,7˚) = 1,17сos14,52˚ =1,13.

Уравнение мощности генератора с АРВ ПД:

=-=

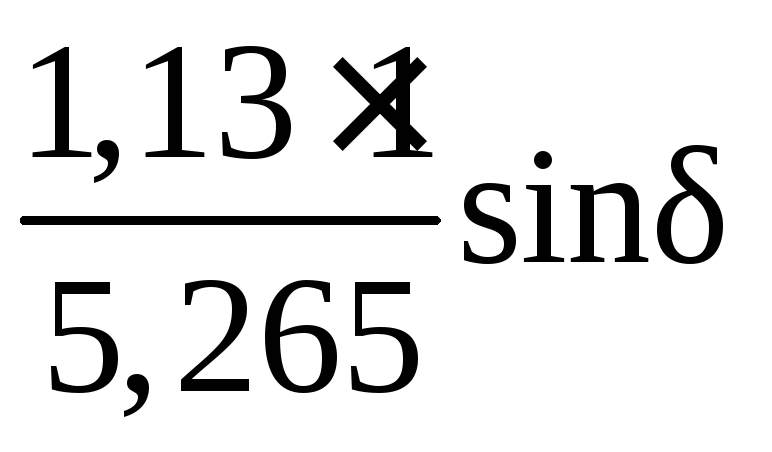=-= 0,21sin - 0,067sin2.

Найдем производнуюи приравняем её нулю:

= 0,21сos - 20,067сos2 = 0,21сos - 0,134сos2 =

= 0,21сos - 0,134(2сos² - 1) = 0,21сos - 0,27сos² + 0,134 = 0,

или 0,27сos² - 0,21сos - 0,134 = 0.

Решим квадратное уравнение относительно сos:

сos_1,2 = [(0,21) (- 0,21)² - 40,27(- 0,134)]/20,27 = (0,21  0,44)/0,54;

сos₁ = 1,22; сos₂ = - 0,4; _пр = 113,5.

Подставим _пр = 113,5 в уравнение мощности:

P_пр = 0,21sin113,5 - 0,067sin2113,5 = 0,210,9 + 0,067(0,73) = 0,239.

Коэффициент запаса статической устойчивости системы равен

К_з = _.

б) генератор имеет АРВ сильного действия

Предел передаваемой мощности определяется исходя из условия постоянства напряжения генератора по поперечной оси U_гq = постоянно.

Напряжение генератора:

U_г =

где X_с* = Х_т1* + Х_т2* + Х_л* = 0,84 + 0,84 +1,99 = 3,665.

Угол между векторами U_гq* и U_с*:

_0с = arctg.

Напряжение генератора по продольной оси

U_гq = U_гсos(₀ - _0с) = 1,12 сos(31,22˚ – 9,47˚) = 1,12сos21,75 = 1,04.

Уравнение мощности генератора с АРВ сильного действия:

P =-=

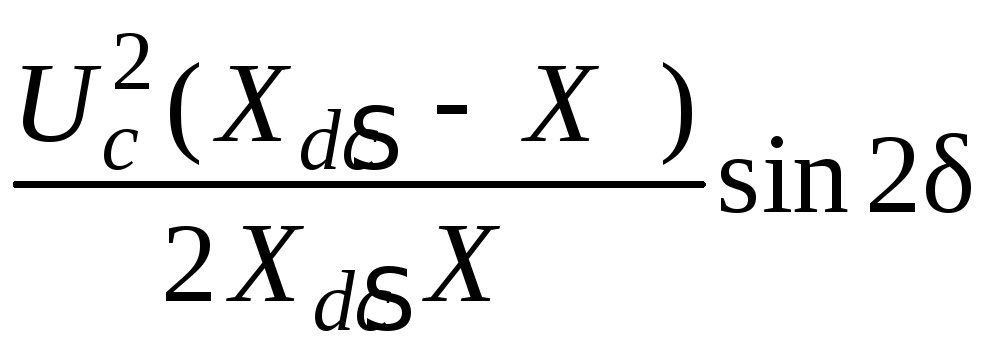₌ - = 0,28sin - 0,11sin2.

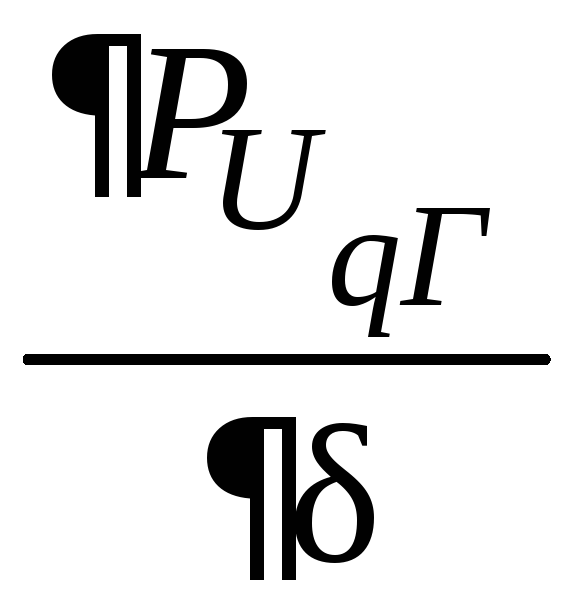= 0,28сos - 20,11сos2 = 0,28сos - 0,22сos2 = 0,28сos -

0,22(2сos² - 1) = 0,28сos - 0,44сos² + 0,22 = 0

или 0,44сos² - 0,28сos - 0,22 = 0.

Решим квадратное уравнение относительно сos:

сos_1,2 = [-(-0,28) (-0,28)² - 40,44(-0,22)]/20,44 = (0,28  0,69)/0,88 ;

сos₁ = 1,14; сos₂ = - 0,43; _пр = 116,5.

Предел передаваемой мощности

P_пр = 0,28sin116,5 - 0,11sin2116,5 = 0,280,895 - 0,11(-0,79) = 0,337.

Коэффициент запаса статической устойчивости системы

К_з =

Вывод:наличие АРВ у генератора повышает статическую устойчивость системы.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4

ТЕМА. ИССЛЕДОВАНИЕ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ ДВУХ СТАНЦИЙ, РАБОТАЮЩИХ НА ОБЩУЮ НАГРУЗКУ