2. Графики

1. За­да­ние 1 № 101. Может ли гра­фик за­ви­си­мо­сти пути от вре­ме­ни иметь сле­ду­ю­щий вид?

 

 

1) да

2) нет

3) может, если тра­ек­то­рия пря­мо­ли­ней­ная

4) может, если тело воз­вра­ща­ет­ся в ис­ход­ную точку

Ре­ше­ние.

Путь — это фи­зи­че­ская ве­ли­чи­на, по­ка­зы­ва­ю­щая прой­ден­ное телом рас­сто­я­ние. Иначе го­во­ря, это длина прой­ден­но­го участ­ка тра­ек­то­рии. По опре­де­ле­нию, путь есть ве­ли­чи­на по­ло­жи­тель­ная, ко­то­рая может толь­ко воз­рас­тать со вре­ме­нем, так что пред­став­лен­ный гра­фик не может изоб­ра­жать за­ви­си­мость пути от вре­ме­ни.

Пра­виль­ный ответ: 2.

Ответ: 2

101

2

2. За­да­ние 1 № 102. Мяч, бро­шен­ный вер­ти­каль­но вверх, па­да­ет на землю. Най­ди­те гра­фик за­ви­си­мо­сти от вре­ме­ни про­ек­ции ско­ро­сти на вер­ти­каль­ную ось, на­прав­лен­ную вверх.

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Мяч после брос­ка дви­жет­ся с по­сто­ян­ным уско­ре­ни­ем сво­бод­но­го па­де­ния, на­прав­лен­ным вниз. Сле­до­ва­тель­но, про­ек­ция ско­рости долж­на умень­шать­ся со вре­ме­нем по ли­ней­но­му за­ко­ну, , гра­фик за­ви­си­мо­сти её от вре­ме­ни пред­став­лен на ри­сун­ке 2.

Пра­виль­ный ответ: 2.

Ответ: 2

102

2

3. За­да­ние 1 № 103. Мяч бро­шен с вер­ши­ны скалы без на­чаль­ной ско­ро­сти. Най­ди­те гра­фик за­ви­си­мо­сти мо­ду­ля пе­ре­ме­ще­ния от вре­ме­ни. Со­про­тив­ле­ни­ем воз­ду­ха пре­не­бречь.

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

По­сколь­ку мяч бро­шен с вер­ши­ны скалы без на­чаль­ной ско­ро­сти, а со­про­тив­ле­ни­ем воз­ду­ха можно пре­не­бречь, за­ви­си­мость мо­ду­ля пе­ре­ме­ще­ния от вре­ме­ни долж­на иметь сле­ду­ю­щий вид:

.

Ис­ко­мая за­ви­си­мость пред­став­ле­на на ри­сун­ке 4. Кроме того, мо­дуль есть ве­ли­чи­на по­ло­жи­тель­ная, этому кри­те­рию также удо­вле­тво­ря­ет толь­ко гра­фик под но­ме­ром 4.

Пра­виль­ный ответ: 4.

Ответ: 4

103

4

4. За­да­ние 1 № 104. Ав­то­мо­биль дви­жет­ся по пря­мой улице. На гра­фи­ке пред­став­ле­на за­ви­си­мость ско­ро­сти ав­то­мо­би­ля от вре­ме­ни.

 

В каком ин­тер­ва­ле вре­ме­ни мак­си­ма­лен мо­дуль уско­ре­ния?

 

1) от 0 до 10 с

2) от 10 до 20 с

3) от 20 до 30 с

4) от 30 до 40 с

Ре­ше­ние.

На всех рас­смат­ри­ва­е­мых ин­тер­ва­лах вре­ме­ни ско­рость ав­то­мо­би­ля ме­ня­ет­ся рав­но­мер­но, сле­до­ва­тель­но уско­ре­ние на каж­дом ин­тер­ва­ле по­сто­ян­но. Все ис­сле­ду­е­мые ин­тер­ва­лы оди­на­ко­вы по дли­тель­но­сти, по­это­му мак­си­маль­но­му мо­ду­лю уско­ре­ния со­от­вет­ству­ет мак­си­маль­ный мо­дуль из­ме­не­ния ско­ро­сти в те­че­ние ин­тер­ва­ла (самый боль­шой угол на­кло­на). Из гра­фи­ка видно, что это ин­тер­вал от 10 до 20 с.

Пра­виль­ный ответ: 2.

Ответ: 2

104

2

5. За­да­ние 1 № 106. По гра­фи­ку за­ви­си­мо­сти мо­ду­ля ско­ро­сти тела от вре­ме­ни, пред­став­лен­но­го на ри­сун­ке, опре­де­ли­те путь, прой­ден­ный телом от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 2 с.

 

1) 1 м

2) 2 м

3) 3 м

4) 4 м

 

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный телом за не­ко­то­рый ин­тер­вал вре­ме­ни, не­об­хо­ди­мо вы­чис­лить пло­щадь под ча­стью гра­фи­ка, со­от­вет­ству­ю­щей этому ин­тер­ва­лу вре­ме­ни (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). В ин­тер­ва­ле вре­ме­ни от 0 С до 2 с ав­то­мо­биль про­шел путь

.

При­ме­ча­ние: В прин­ци­пе, ин­те­ре­су­ю­щий нас уча­сток (от 0 до 2 с) не обя­за­тель­но раз­би­вать на два, пло­щадь под гра­фи­ком можно по­счи­тать, как пло­щадь тра­пе­ции:

.

Пра­виль­ный ответ: 3.

Ответ: 3

106

3

6. За­да­ние 1 № 107. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти мо­ду­ля ско­ро­сти ав­то­мо­би­ля от вре­ме­ни. Опре­де­ли­те по гра­фи­ку путь, прой­ден­ный ав­то­мо­би­лем в ин­тер­ва­ле от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 5 с после на­ча­ла от­сче­та вре­ме­ни.

 

 

1) 6 м

2) 15 м

3) 17 м

4) 23 м

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный ав­то­мо­би­лем за не­ко­то­рый ин­тер­вал вре­ме­ни, не­об­хо­ди­мо вы­чис­лить пло­щадь под ча­стью гра­фи­ка, со­от­вет­ству­ю­щей этому ин­тер­ва­лу вре­ме­ни (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). В ин­тер­ва­ле от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 5 с после на­ча­ла дви­же­ния ав­то­мо­биль про­шел путь

 

.

Дру­гой спо­соб ре­ше­ния за­клю­ча­ет­ся в ана­ли­зе каж­до­го участ­ка гра­фи­ка в от­дель­но­сти, опре­де­ле­ния из гра­фи­ка на­чаль­ных ско­ро­стей и уско­ре­ний на каж­дом этапе и ис­поль­зо­ва­ния стан­дарт­ных ки­не­ма­ти­че­ских фор­мул для пути.

Пра­виль­ный ответ: 3.

Ответ: 3

107

3

7. За­да­ние 1 № 108. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти мо­ду­ля ско­ро­сти тела от вре­ме­ни.

 

Какой путь прой­ден телом за вто­рую се­кун­ду?

 

1) 0 м

2) 1 м

3) 2 м

4) 3 м

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный телом за не­ко­то­рый ин­тер­вал вре­ме­ни, не­об­хо­ди­мо вы­чис­лить пло­щадь под ча­стью гра­фи­ка, со­от­вет­ству­ю­щей этому ин­тер­ва­лу вре­ме­ни (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). За вто­рую се­кун­ду ав­то­мо­биль про­шел путь

 

.

Пра­виль­ный ответ: 3.

Ответ: 3

108

3

8. За­да­ние 1 № 109. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти мо­ду­ля ско­ро­сти тела от вре­ме­ни.

 

Най­ди­те путь, прой­ден­ный телом за время от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 5 с.

 

1) 0 м

2) 15 м

3) 20 м

4) 30 м

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный телом за не­ко­то­рый ин­тер­вал вре­ме­ни, не­об­хо­ди­мо вы­чис­лить пло­щадь под ча­стью гра­фи­ка, со­от­вет­ству­ю­щей этому ин­тер­ва­лу вре­ме­ни (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). В ин­тер­ва­ле от мо­мен­та вре­ме­ни 0 с до мо­мен­та вре­ме­ни 5 с после на­ча­ла дви­же­ния тело про­шло путь

 

.

Дру­гой спо­соб ре­ше­ния за­клю­ча­ет­ся в ана­ли­зе каж­до­го участ­ка гра­фи­ка в от­дель­но­сти, опре­де­ле­ния из гра­фи­ка на­чаль­ных ско­ро­стей и уско­ре­ний на каж­дом этапе и ис­поль­зо­ва­ния стан­дарт­ных ки­не­ма­ти­че­ских фор­мул для пути.

Пра­виль­ный ответ: 3.

Ответ: 3

109

3

9. За­да­ние 1 № 110. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти пути от вре­ме­ни.

 

Опре­де­ли­те по гра­фи­ку ско­рость дви­же­ния ве­ло­си­пе­ди­ста в ин­тер­ва­ле от мо­мен­та вре­ме­ни 1 с до мо­мен­та вре­ме­ни 3 с после на­ча­ла дви­же­ния.

 

1)

2)

3)

4)

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле от мо­мен­та вре­ме­ни 1 с до мо­мен­та вре­ме­ни 3 с после на­ча­ла дви­же­ния путь ве­ло­си­пе­ди­ста не из­ме­нял­ся. Сле­до­ва­тель­но на этом ин­тер­ва­ле вре­ме­ни ве­ло­си­пе­дист не дви­гал­ся, его ско­рость была равна нулю.

Пра­виль­ный ответ: 1.

Ответ: 1

110

1

10. За­да­ние 1 № 116. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком гра­фи­ке пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 10 до 20 с?

 

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 10 до 20 с про­ек­ция ско­ро­сти тела не из­ме­ня­лась, а зна­чит, про­ек­ция уско­ре­ния была равна нулю. Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 2.

Пра­виль­ный ответ: 2.

Ответ: 2

116

2

11. За­да­ние 1 № 117. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 0 до 6 с?

 

 

 

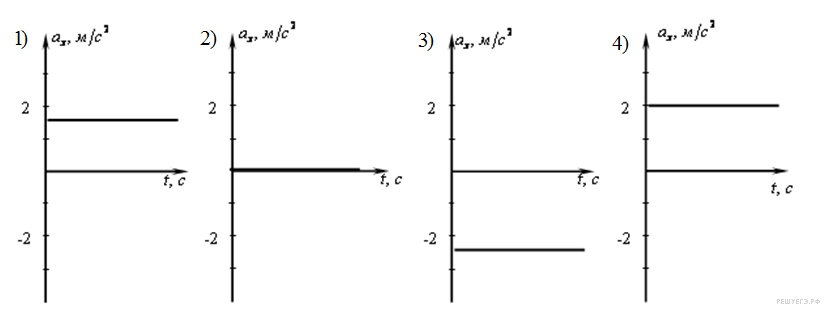
1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что уско­ре­ние в ин­тер­ва­ле вре­ме­ни от 0 с до 10 с по­сто­ян­но. Зна­чит, на этом ин­тер­ва­ле ве­ре­ме­ни уско­ре­ние такое же, как и на ин­тер­ва­ле от 0 с до 6 с. Найдём это уско­ре­ние:

 

.

 

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 1.

 

Ответ: 1.

Ответ: 1

117

1

12. За­да­ние 1 № 118. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 20 до 26 с?

 

 

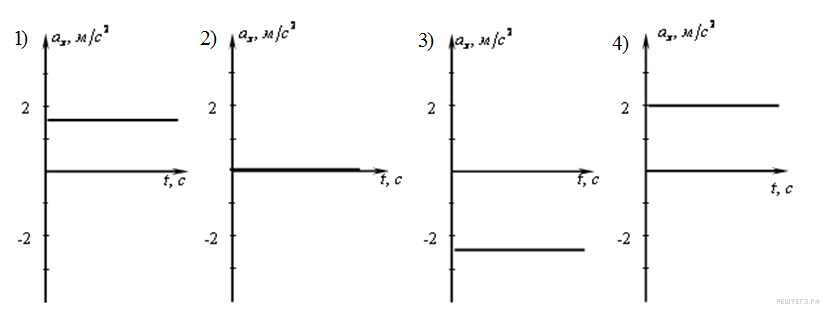
1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 20 до 26 с про­ек­ция ско­ро­сти тела убы­ва­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 3.

Пра­виль­ный ответ: 3.

Ответ: 3

118

3

13. За­да­ние 1 № 119. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

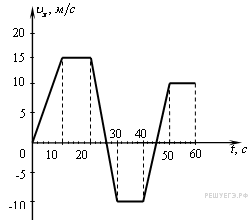
На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 54 до 60 с?

 

 

 

 

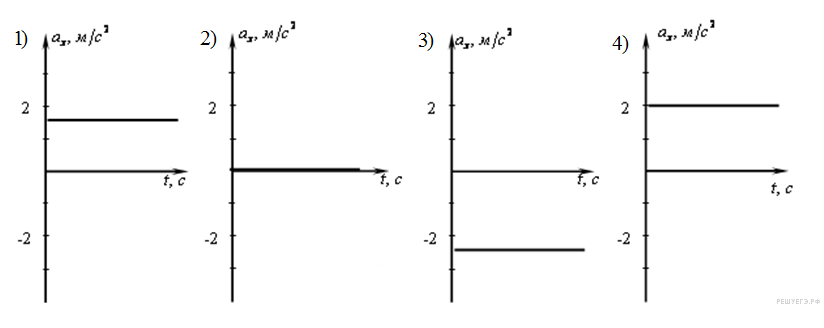
1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 54 до 60 с про­ек­ция ско­ро­сти тела не из­ме­ня­лась, а зна­чит, про­ек­ция уско­ре­ния была равна нулю. Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 2.

Пра­виль­ный ответ: 2.

Ответ: 2

119

2

14. За­да­ние 1 № 120. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 42 до 48 с?

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 42 до 48 с (и даже на более боль­шом ин­тер­ва­ле от 40 с до 50 с) про­ек­ция ско­ро­сти тела воз­рас­та­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 4.

Пра­виль­ный ответ: 4.

 

Ответ: 4

120

4

15. За­да­ние 1 № 121. На ри­сун­ке пред­став­лен гра­фик за­ви­си­мо­сти мо­ду­ля ско­ро­сти ав­то­мо­би­ля от вре­ме­ни t.

 

Най­ди­те путь, прой­ден­ный ав­то­мо­би­лем за 5 c.

 

1) 0 м

2) 20 м

3) 30 м

4) 35 м

Ре­ше­ние.

Для того чтобы по гра­фи­ку мо­ду­ля ско­ро­сти найти путь, прой­ден­ный телом, не­об­хо­ди­мо вы­чис­лить пло­щадь под гра­фи­ком (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). За 5 c ав­то­мо­биль про­шел путь

.

Дру­гой спо­соб ре­ше­ния за­клю­ча­ет­ся в ана­ли­зе каж­до­го участ­ка гра­фи­ка в от­дель­но­сти, опре­де­ле­ния из гра­фи­ка на­чаль­ных ско­ро­стей и уско­ре­ний на каж­дом этапе и ис­поль­зо­ва­ния стан­дарт­ных ки­не­ма­ти­че­ских фор­мул для пути.

Пра­виль­ный ответ: 4.

Ответ: 4

121

4

16. За­да­ние 1 № 122. Ав­то­мо­биль дви­жет­ся по пря­мой улице. На гра­фи­ке пред­став­ле­на за­ви­си­мость его ско­ро­сти от вре­ме­ни.

 

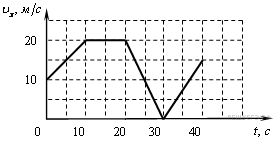
На каком ин­тер­ва­ле вре­ме­ни мо­дуль уско­ре­ния ав­то­мо­би­ля мак­си­ма­лен?

 

1) от 0 с до 10 с

2) от 10 с до 20 с

3) от 20 с до 30 с

4) от 30 с до 40 с

Ре­ше­ние.

На всех рас­смат­ри­ва­е­мых ин­тер­ва­лах вре­ме­ни ско­рость ав­то­мо­би­ля ме­ня­ет­ся рав­но­мер­но, сле­до­ва­тель­но, уско­ре­ние на каж­дом ин­тер­ва­ле по­сто­ян­но. Все ис­сле­ду­е­мые ин­тер­ва­лы оди­на­ко­вы по дли­тель­но­сти, по­это­му мак­си­маль­но­му мо­ду­лю уско­ре­ния со­от­вет­ству­ет мак­си­маль­ный мо­дуль из­ме­не­ния ско­ро­сти в те­че­ние ин­тер­ва­ла: . Из гра­фи­ка видно, что это ин­тер­вал от 20 до 30 с

(в этом слу­чае , на дру­гих ин­тер­ва­лах мень­ше).

Пра­виль­ный ответ: 3.

Ответ: 3

122

3

17. За­да­ние 1 № 128. Тело дви­жет­ся по оси Ox. На гра­фи­ке по­ка­за­на за­ви­си­мость про­ек­ции ско­ро­сти тела на ось Ox от вре­ме­ни.

 

Каков путь, прой­ден­ный телом к мо­мен­ту вре­ме­ни

 

1) 6 м

2) 8 м

3) 4 м

4) 5 м

Ре­ше­ние.

На про­тя­же­нии всего ин­тер­ва­ла вре­ме­ни про­ек­ция ско­ро­сти тела на ось Ox по­ло­жи­тель­на. По­это­му, для того чтобы найти путь, прой­ден­ный телом, не­об­хо­ди­мо вы­чис­лить пло­щадь под гра­фи­ком (в еди­ни­цах про­из­ве­де­ния ве­ли­чин, от­ло­жен­ных по осям ко­ор­ди­нат). К мо­мен­ту вре­ме­ни тело про­шло путь

.

Дру­гой спо­соб ре­ше­ния за­клю­ча­ет­ся в ана­ли­зе каж­до­го участ­ка гра­фи­ка в от­дель­но­сти, опре­де­ле­ния из гра­фи­ка на­чаль­ных ско­ро­стей и уско­ре­ний на каж­дом этапе и ис­поль­зо­ва­ния стан­дарт­ных ки­не­ма­ти­че­ских фор­мул для пути.

Пра­виль­ный ответ: 1.

Ответ: 1

128

1

18. За­да­ние 1 № 130. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

С каким из гра­фи­ков сов­па­да­ет гра­фик за­ви­си­мо­сти от вре­ме­ни про­ек­ции уско­ре­ния этого тела в ин­тер­ва­ле вре­ме­ни от 10 до 15 с?

 

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 10 до 15 с про­ек­ция ско­ро­сти тела воз­рас­та­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 3.

Пра­виль­ный ответ: 3.

Ответ: 3

130

3

19. За­да­ние 1 № 132. Ав­то­мо­биль дви­жет­ся пря­мо­ли­ней­но. На гра­фи­ке пред­став­ле­на за­ви­си­мость ско­ро­сти ав­то­мо­би­ля от вре­ме­ни.

 

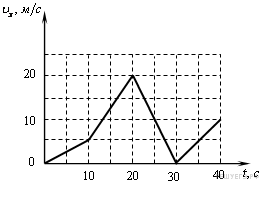
На каком ин­тер­ва­ле вре­ме­ни мо­дуль его уско­ре­ния ми­ни­ма­лен?

 

1) от 0 до 10 с

2) от 10 с до 20 с

3) от 20 с до 30 с

4) от 30 до 40 с

Ре­ше­ние.

На всех рас­смат­ри­ва­е­мых ин­тер­ва­лах вре­ме­ни ско­рость ав­то­мо­би­ля ме­ня­ет­ся рав­но­мер­но, сле­до­ва­тель­но уско­ре­ние на каж­дом ин­тер­ва­ле по­сто­ян­но. Все ис­сле­ду­е­мые ин­тер­ва­лы оди­на­ко­вы по дли­тель­но­сти, по­это­му ми­ни­маль­но­му мо­ду­лю уско­ре­ния со­от­вет­ству­ет ми­ни­маль­ный мо­дуль из­ме­не­ния ско­ро­сти в те­че­ние ин­тер­ва­ла. Из гра­фи­ка видно, что это ин­тер­вал от 0 до 10 с.

Пра­виль­ный ответ: 1.

Ответ: 1

132

1

20. За­да­ние 1 № 136. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 24 до 30 с?

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 24 до 30 с про­ек­ция ско­ро­сти тела убы­ва­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 3.

Пра­виль­ный ответ: 3.

Ответ: 3

136

3

21. За­да­ние 1 № 137. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

На каком из гра­фи­ков пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 4 до 10 с?

 

 

 

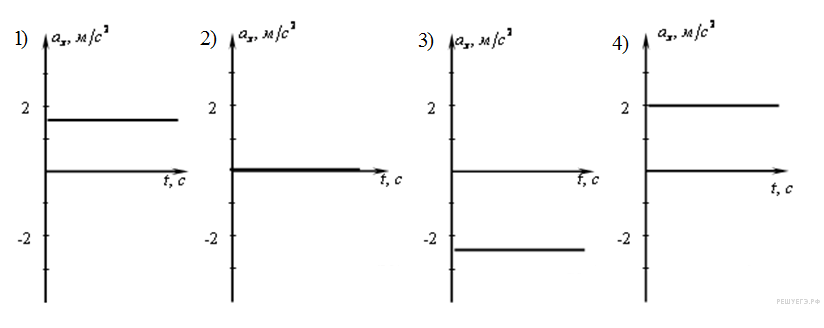
1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 0 до 6 с про­ек­ция ско­ро­сти тела воз­рас­та­ла ли­ней­но со вре­ме­нем, а зна­чит, про­ек­ция уско­ре­ния была по­сто­ян­на и рав­ня­лась

.

Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 1.

Пра­виль­ный ответ: 1.

Ответ: 1

137

1

22. За­да­ние 1 № 138. На ри­сун­ке при­ве­ден гра­фик за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни.

 

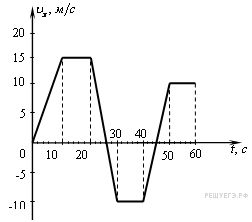
На каком гра­фи­ке пред­став­ле­на про­ек­ция уско­ре­ния тела в ин­тер­ва­ле вре­ме­ни от 30 до 40 с?

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из гра­фи­ка видно, что в ин­тер­ва­ле вре­ме­ни от 30 до 40 с про­ек­ция ско­ро­сти тела не из­ме­ня­лась, а зна­чит, про­ек­ция уско­ре­ния была равна нулю. Про­ек­ция уско­ре­ния тела в этом ин­тер­ва­ле вре­ме­ни пред­став­ле­на на гра­фи­ке 2.

Пра­виль­ный ответ: 2.

Ответ: 2

138

2

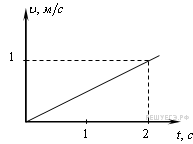
23. За­да­ние 1 № 140. Тело на­чи­на­ет дви­гать­ся из на­ча­ла ко­ор­ди­нат вдоль оси Ox, при­чем про­ек­ция ско­ро­сти ме­ня­ет­ся с те­че­ни­ем вре­ме­ни по за­ко­ну, при­ве­ден­но­му на гра­фи­ке.

 

Чему будет равна про­ек­ция уско­ре­ния тела через 2 c?

 

1)

2)

3)

4)

Ре­ше­ние.

Из гра­фи­ка видно, что про­ек­ция ско­ро­сти тела воз­рас­та­ла со вре­ме­нем по ли­ней­но­му за­ко­ну, это озна­ча­ет, что тело дви­га­лось с по­сто­ян­ным уско­ре­ни­ем вдоль оси Ox. Таким об­ра­зом, про­ек­ция уско­ре­ния тела через 2 c равна

 

.

Пра­виль­ный ответ: 2.

Ответ: 2

140

2

24. За­да­ние 1 № 3323. 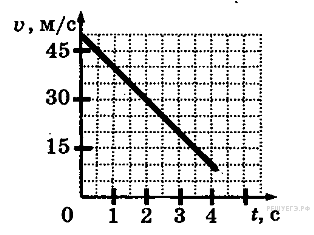На гра­фи­ке при­ве­де­на за­ви­си­мость ско­ро­сти пря­мо­ли­ней­но­го дви­жу­ще­го­ся тела от вре­ме­ни. Опре­де­ли­те мо­дуль уско­ре­ния тела.

 

1)

2)

3)

4)

Ре­ше­ние.

Из гра­фи­ка видно, что ско­рость тела за­ви­сит ли­ней­но от вре­ме­ни, а зна­чит, его уско­ре­ние по­сто­ян­но. Для опре­де­ле­ния мо­ду­ля уско­ре­ния можно взять любые две точки на гра­фи­ке: .

 

Ответ: 1.

Ответ: 1

3323

1

25. За­да­ние 1 № 3324. 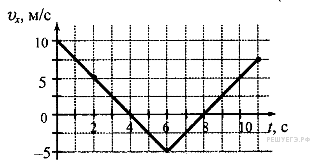Тело дви­жет­ся по оси х. По гра­фи­ку за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни t уста­но­ви­те, какой путь про­шло тело за время от до .

 

1) 10 м

2) 15 м

3) 45 м

4) 20 м

Ре­ше­ние.

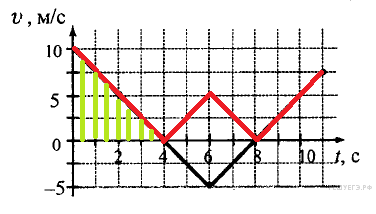Не­об­хо­ди­мо раз­ли­чать два по­ня­тия: путь и пе­ре­ме­ще­ние. Путь — ве­ли­чи­на стро­го по­ло­жи­тель­ная, это длина прой­ден­но­го телом участ­ка тра­ек­то­рии. Под пе­ре­ме­ще­ни­ем же тела по­ни­ма­ет­ся из­ме­не­ние его ко­ор­ди­на­ты, пе­ре­ме­ще­ние может быть от­ри­ца­тель­ным. Прой­ден­ный телом путь опре­де­ля­ет­ся за­ви­си­мо­стью от вре­ме­ни мо­ду­ля ско­ро­сти. Чтобы из гра­фи­ка за­ви­си­мо­сти про­ек­ции ско­ро­сти тела от вре­ме­ни по­лу­чить гра­фик мо­ду­ля ско­ро­сти, не­об­хо­ди­мо зер­каль­но от­ра­зить от­но­си­тель­но го­ри­зон­таль­но оси все от­ри­ца­тель­ные участ­ки. В дан­ной за­да­че это не столь прин­ци­пи­аль­но, по­сколь­ку на рас­смат­ри­ва­ем ин­тер­ва­ле от до про­ек­ция ско­ро­сти тела оста­ет­ся по­ло­жи­тель­ной, но в общем слу­чае это может при­ве­сти к не­же­ла­тель­ной ошиб­ке.