Закон Всемирного тяготения

Закон Все­мир­но­го тяготения

1. За­да­ние 4 № 209. Ме­тео­рит про­ле­та­ет около Земли за пре­де­ла­ми ат­мо­сфе­ры. Как на­прав­лен век­тор уско­ре­ния ме­тео­ри­та в тот мо­мент, когда век­тор силы гра­ви­та­ци­он­но­го при­тя­же­ния Земли пер­пен­ди­ку­ля­рен век­то­ру ско­ро­сти ме­тео­ри­та?

 

1) па­рал­лель­но век­то­ру ско­ро­сти

2) по на­прав­ле­нию век­то­ра силы

3) по на­прав­ле­нию век­то­ра ско­ро­сти

4) по на­прав­ле­нию суммы век­то­ров силы и ско­ро­сти

Ре­ше­ние.

Со­глас­но вто­ро­му за­ко­ну Нью­то­на, уско­ре­ние тела со­на­прав­ле­но с рав­но­дей­ству­ю­щей всех сил. По­сколь­ку ме­тео­рит про­ле­та­ет около Земли за пре­де­ла­ми ат­мо­сфе­ры, на него дей­ству­ет толь­ко сила гра­ви­та­ци­он­но­го при­тя­же­ния со сто­ро­ны Земли. Таким об­ра­зом, век­тор уско­ре­ния ме­тео­ри­та на­прав­лен по на­прав­ле­нию век­то­ра силы.

Пра­виль­ный ответ: 2.

Ответ: 2

209

2

2. За­да­ние 4 № 210. Кос­ми­че­ский ко­рабль уле­та­ет от Земли с вы­клю­чен­ны­ми дви­га­те­ля­ми. Как на­прав­лен век­тор уско­ре­ния ко­раб­ля в тот мо­мент, когда век­тор силы гра­ви­та­ци­он­но­го при­тя­же­ния Земли на­прав­лен под углом к век­то­ру ско­ро­сти ко­раб­ля? Дей­ствие осталь­ных тел на ко­рабль пре­не­бре­жи­мо мало.

 

1) по на­прав­ле­нию век­то­ра ско­ро­сти

2) по на­прав­ле­нию век­то­ра силы

3) про­ти­во­по­лож­но век­то­ру ско­ро­сти

4) по на­прав­ле­нию суммы век­то­ров силы и ско­ро­сти

Ре­ше­ние.

Со­глас­но вто­ро­му за­ко­ну Нью­то­на, уско­ре­ние тела со­на­прав­ле­но с рав­но­дей­ству­ю­щей всех сил. По­сколь­ку дей­стви­ем осталь­ных тел на ко­рабль можно пре­не­бречь, на него дей­ству­ет толь­ко сила гра­ви­та­ци­он­но­го при­тя­же­ния со сто­ро­ны Земли. Таким об­ра­зом, век­тор уско­ре­ния ко­раб­ля на­прав­лен по на­прав­ле­нию век­то­ра силы.

Пра­виль­ный ответ: 2.

Ответ: 2

210

2

3. За­да­ние 4 № 301. Две пла­не­ты с оди­на­ко­вы­ми мас­са­ми об­ра­ща­ют­ся по кру­го­вым ор­би­там во­круг звез­ды. У пер­вой из них ра­ди­ус ор­би­ты вдвое боль­ше, чем у вто­рой. Ка­ко­во от­но­ше­ние сил при­тя­же­ния пер­вой и вто­рой пла­нет к звез­де ?

 

1) 0,25

2) 2

3) 0,5

4) 4

Ре­ше­ние.

По за­ко­ну Все­мир­но­го тя­го­те­ния сила при­тя­же­ния пла­не­ты к звез­де об­рат­но про­пор­ци­о­наль­на квад­ра­ту ра­ди­у­са ор­би­ты. Таким об­ра­зом, в силу ра­вен­ства масс от­но­ше­ние сил при­тя­же­ния к звез­де пер­вой и вто­рой пла­нет об­рат­но про­пор­ци­о­наль­но от­но­ше­нию квад­ра­тов ра­ди­у­сов орбит:

.

По усло­вию, у пер­вой пла­не­ты ра­ди­ус ор­би­ты вдвое боль­ше, чем у вто­рой, то есть , а зна­чит,

.

Ответ: 1

301

1

4. За­да­ние 4 № 304. Две пла­не­ты с оди­на­ко­вы­ми мас­са­ми об­ра­ща­ют­ся по кру­го­вым ор­би­там во­круг звез­ды. Для пер­вой из них сила при­тя­же­ния к звез­де в 9 раз мень­ше, чем для вто­рой. Ка­ко­во от­но­ше­ние ра­ди­у­сов орбит пер­вой и вто­рой пла­нет?

 

1)

2)

3)

4)

Ре­ше­ние.

По за­ко­ну Все­мир­но­го тя­го­те­ния сила при­тя­же­ния пла­не­ты к звез­де об­рат­но про­пор­ци­о­наль­на квад­ра­ту ра­ди­у­са ор­би­ты. Таким об­ра­зом, в силу ра­вен­ства масс от­но­ше­ние сил при­тя­же­ния к звез­де пер­вой и вто­рой пла­нет об­рат­но про­пор­ци­о­наль­но от­но­ше­нию квад­ра­тов ра­ди­у­сов орбит:

.

По усло­вию, сила при­тя­же­ния для пер­вой пла­не­ты к звез­де в 9 раза мень­ше, чем для вто­рой: а зна­чит,

.

Ответ: 3

304

3

5. За­да­ние 4 № 305. У по­верх­но­сти Земли на кос­мо­нав­та дей­ству­ет сила тя­го­те­ния 720 Н. Какая сила тя­го­те­ния дей­ству­ет со сто­ро­ны Земли на того же кос­мо­нав­та в кос­ми­че­ском ко­раб­ле, дви­жу­щем­ся по кру­го­вой ор­би­те во­круг Земли на рас­сто­я­нии трех зем­ных ра­ди­у­сов от ее цен­тра?

 

1) 0 H

2) 240 H

3) 180 H

4) 80 H

Ре­ше­ние.

По за­ко­ну Все­мир­но­го тя­го­те­ния сила при­тя­же­ния кос­мо­нав­та со сто­ро­ны Земли об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ним и цен­тром Земли: . У по­верх­но­сти Земли это рас­сто­я­ние сов­па­да­ет с ра­ди­у­сом пла­не­ты (). На кос­ми­че­ском ко­раб­ле, по усло­вию, оно в три раза боль­ше (). Таким об­ра­зом, сила тя­го­те­ния со сто­ро­ны Земли, дей­ству­ю­щая на кос­мо­нав­та на кос­ми­че­ском ко­раб­ле, в 9 раз мень­ше, чем у по­верх­но­сти Земли, то есть

.

Ответ: 4

305

4

6. За­да­ние 4 № 306. У по­верх­но­сти Луны на кос­мо­нав­та дей­ству­ет сила тя­го­те­ния 144 Н. Какая сила тя­го­те­ния дей­ству­ет со сто­ро­ны Луны на того же кос­мо­нав­та в кос­ми­че­ском ко­раб­ле, дви­жу­щем­ся по кру­го­вой ор­би­те во­круг Луны на рас­сто­я­нии трех лун­ных ра­ди­у­сов от ее цен­тра?

 

1) 48 H

2) 36 H

3) 16 H

4) 0 H

Ре­ше­ние.

По за­ко­ну Все­мир­но­го тя­го­те­ния сила при­тя­же­ния кос­мо­нав­та со сто­ро­ны Луны об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ним и цен­тром Луны. У по­верх­но­сти Луны это рас­сто­я­ние сов­па­да­ет с ра­ди­у­сом спут­ни­ка. На кос­ми­че­ском ко­раб­ле, по усло­вию, оно в три раза боль­ше. Таким об­ра­зом, сила тя­го­те­ния со сто­ро­ны Луны, дей­ству­ю­щая на кос­мо­нав­та на кос­ми­че­ском ко­раб­ле, в 9 раз мень­ше, чем у по­верх­но­сти Луны, то есть

.

Ответ: 3

306

3

7. За­да­ние 4 № 307. Кос­ми­че­ская ра­ке­та стар­ту­ет с по­верх­но­сти Луны и дви­жет­ся вер­ти­каль­но вверх. На каком рас­сто­я­нии от лун­ной по­верх­но­сти сила гра­ви­та­ци­он­но­го при­тя­же­ния ра­ке­ты Луной умень­шит­ся в 4 раза по срав­не­нию с силой при­тя­же­ния на лун­ной по­верх­но­сти? (Рас­сто­я­ние вы­ра­жа­ет­ся в ра­ди­у­сах Луны R).

Из­ме­не­ни­ем массы ра­ке­ты из-за рас­хо­да топ­ли­ва пре­не­бречь.

 

1)

2)

3)

4)

Ре­ше­ние.

Если пре­не­бречь из­ме­не­ни­ем массы ра­ке­ты, вы­зван­ным рас­хо­дом топ­ли­ва на взлет, то ре­ше­ние вы­гля­дит сле­ду­ю­щим об­ра­зом. Сила гра­ви­та­ци­он­но­го при­тя­же­ния ра­ке­ты Луной по за­ко­ну Все­мир­но­го тя­го­те­ния об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ра­ке­той и цен­тром Луны. На лун­ной по­верх­но­сти это рас­сто­я­ние сов­па­да­ет с ра­ди­у­сом Луны R. Для того чтобы сила при­тя­же­ния умень­ши­лась в 4 раза при не­из­мен­ной массе ра­ке­ты, рас­сто­я­ние долж­но уве­ли­чить­ся в 2 раза, то есть стать рав­ным 2R. Сле­до­ва­тель­но, не­об­хо­ди­мо под­нять­ся на вы­со­ту над по­верх­но­стью Луны.

 

Пра­виль­ный ответ: 1.

Ответ: 1

307

1

8. За­да­ние 4 № 326. Два ма­лень­ких ша­ри­ка мас­сой m каж­дый на­хо­дят­ся на рас­сто­я­нии r друг от друга и при­тя­ги­ва­ют­ся с силой F. Ка­ко­ва сила гра­ви­та­ци­он­но­го при­тя­же­ния двух дру­гих ша­ри­ков, если масса каж­до­го из них , а рас­сто­я­ние между их цен­тра­ми 2r?

 

1)

2)

3)

4)

Ре­ше­ние.

Со­глас­но за­ко­ну Все­мир­но­го тя­го­те­ния, сила при­тя­же­ния двух тел про­пор­ци­о­наль­на про­из­ве­де­нию их масс и об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ними: . Таким об­ра­зом, ша­ри­ки, име­ю­щие в 2 раза мень­шую массу и от­не­сен­ные на в 2 раза боль­шее рас­сто­я­ние, при­тя­ги­ва­ют­ся в 16 раз сла­бее, сила их при­тя­же­ния равна .

Пра­виль­ный ответ: 4.

Ответ: 4

326

4

9. За­да­ние 4 № 331. Два ма­лень­ких ша­ри­ка мас­сой m каж­дый на­хо­дят­ся на рас­сто­я­нии r друг от друга и при­тя­ги­ва­ют­ся с силой F. Чему равна сила гра­ви­та­ци­он­но­го при­тя­же­ния двух дру­гих ша­ри­ков, если масса каж­до­го , а рас­сто­я­ние между ними ?

 

1)

2)

3)

4)

Ре­ше­ние.

Со­глас­но за­ко­ну Все­мир­но­го тя­го­те­ния, сила при­тя­же­ния двух тел про­пор­ци­о­наль­на про­из­ве­де­нию их масс и об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ними: . Таким об­ра­зом, ша­ри­ки, име­ю­щие в 3 раза мень­шую массу и от­не­сен­ные на в 3 раза мень­шее рас­сто­я­ние, при­тя­ги­ва­ют­ся с такой же силой F.

 

Ответ: 3.

Ответ: 3

331

3

10. За­да­ние 4 № 332. Кос­мо­навт на Земле при­тя­ги­ва­ет­ся к ней с силой 700 Н. С какой при­бли­зи­тель­но силой он будет при­тя­ги­вать­ся к Марсу, на­хо­дясь на его по­верх­но­сти, если ра­ди­ус Марса в 2 раза мень­ше, а масса — в 10 раз мень­ше, чем у Земли?

 

1) 70 Н

2) 140 Н

3) 210 Н

4) 280 Н

Ре­ше­ние.

Со­глас­но за­ко­ну Все­мир­но­го тя­го­те­ния, сила при­тя­же­ния двух тел про­пор­ци­о­наль­на про­из­ве­де­нию их масс и об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ними. Таким об­ра­зом, силы при­тя­же­ния кос­мо­нав­та к Земле и Марсу равны и со­от­вет­ствен­но. От­сю­да на­хо­дим при­бли­зи­тель­но силу при­тя­же­ния кос­мо­нав­та к Марсу:

.

Пра­виль­ный ответ: 4.

Ответ: 4

332

4

11. За­да­ние 4 № 3356. Два ма­лень­ких ша­ри­ка на­хо­дят­ся на боль­шом рас­сто­я­нии l друг от друга. На каком рас­сто­я­нии друг от друга на­хо­дят­ся ша­ри­ки с вдвое боль­ши­ми мас­са­ми, если ве­ли­чи­на сил их гра­ви­та­ци­он­но­го при­тя­же­ния такая же?

 

1) 4 l

2) 1/4 l

3) 2 l

4) 1/2 l

Ре­ше­ние.

Со­глас­но за­ко­ну Все­мир­но­го тя­го­те­ния, сила вза­и­мо­дей­ствия тел прямо про­пор­ци­о­наль­на про­из­ве­де­нию их масс и об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ними: . Сле­до­ва­тель­но, для того чтобы тела с вдвое боль­ши­ми мас­са­ми вза­и­мо­дей­ство­ва­ли с той же силой, их не­об­хо­ди­мо раз­ме­стить на вдвое боль­шем рас­сто­я­нии 2l.

 

Ответ: 3.

Ответ: 3

3356

3

12. За­да­ние 4 № 3555. Спут­ник пла­не­ты мас­сой дви­жет­ся по кру­го­вой ор­би­те ра­ди­у­сом . Ка­ко­ва ско­рость дви­же­ния спут­ни­ка?

 

1)

2)

3)

4)

Ре­ше­ние.

На спут­ник дей­ству­ет толь­ко сила при­тя­же­ния со сто­ро­ны пла­не­ты, ко­то­рая, со­глас­но за­ко­ну Все­мир­но­го тя­го­те­ния, равна . Так как по усло­вию спут­ник дви­га­ет­ся по кру­го­вой ор­би­те, он дви­га­ет­ся с по­сто­ян­ным цен­тро­стре­ми­тель­ным уско­ре­ни­ем . Вы­пи­шем вто­рой закон Нью­то­на для спут­ни­ка в про­ек­ции на ра­ди­аль­ную ось:

Пра­виль­ный ответ: 3.

Ответ: 3

3555

3

13. За­да­ние 4 № 3776. Вес тела на по­лю­се пла­не­ты, име­ю­щей форму шара, на 16 про­цен­тов пре­вы­ша­ет вес на эк­ва­то­ре. Если плот­ность пла­не­ты , то пе­ри­од об­ра­ще­ния пла­не­ты равен

 

1)

2)

3)

4)

Ре­ше­ние.

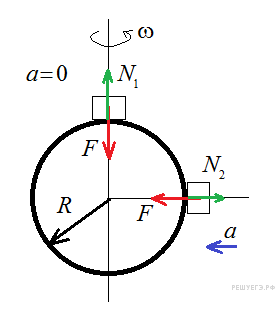Вес P тела — это сила, с ко­то­рой тело давит на опору или рас­тя­ги­ва­ет под­вес. Опре­де­лим, чему равен вес не­ко­то­ро­го тела на по­лю­се и на эк­ва­то­ре. Для опре­де­лен­но­сти рас­смот­рим тело, ле­жа­щее на го­ри­зон­таль­ной опоре (это пред­по­ло­же­ние­не огра­ни­чи­ва­ет общ­ность по­лу­ча­е­мых далее ре­зуль­та­тов).

 

По тре­тье­му за­ко­ну Нью­то­на сила дей­ствия равна силе про­ти­во­дей­ствия, а по­то­му, вес тела равен по ве­ли­чи­не силе ре­ак­ции опоры N, дей­ству­ю­щей на тело. Сле­до­ва­тель­но, до­ста­точ­но срав­нить силы ре­ак­ции опоры в двух слу­ча­ях.

 

Обо­зна­чим массу тела через m. Пусть ра­ди­ус пла­не­ты через R, тогда масса пла­не­ты равна . По­сколь­ку пла­не­та од­но­род­ная и имеет форму сферы, со­глас­но за­ко­ну все­мир­но­го тя­го­те­ния сила при­тя­же­ния тела к пла­не­те в обеих точ­ках оди­на­ко­ва и равна

 

.

Рас­смот­рим слу­чай, когда тело на­хо­дит­ся на по­лю­се. Вто­рой закон Нью­то­на для него в про­ек­ции на ра­ди­аль­ную ось при­об­ре­та­ет вид:

 

.

Когда же тело на­хо­дит­ся на эк­ва­то­ре, оно вра­ща­ет­ся вме­сте с пла­не­той во­круг оси вра­ще­ния, а зна­чит, оно дви­жет­ся с цен­тро­стре­ми­тель­ным уско­ре­ни­ем где  —   уг­ло­вая ско­рость вра­ще­ния пла­не­ты. Сле­до­ва­тель­но, для тела на эк­ва­то­ре вто­рой закон Нью­то­на в про­ек­ции на ра­ди­аль­ную ось при­об­ре­та­ет вид:

 

Со­глас­но усло­вию, , а зна­чит,

 

От­сю­да для пе­ри­о­да об­ра­ще­ния пла­не­ты имеем:

 

 

Пра­виль­ный ответ: 1.

 

Ответ: 1

3776

1

14. За­да­ние 4 № 5955. 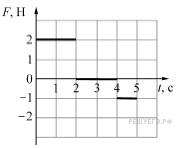Ма­те­ри­аль­ная точка мас­сой 2 кг дви­жет­ся вдоль го­ри­зон­таль­ной оси под дей­стви­ем го­ри­зон­таль­ной силы . В на­чаль­ный мо­мент вре­ме­ни тело по­ко­и­лось. Гра­фик за­ви­си­мо­сти мо­ду­ля силы от вре­ме­ни изоб­ражён на ри­сун­ке. В конце тре­тьей се­кун­ды им­пульс ма­те­ри­аль­ной точки равен

 

1) 0 кг·м/с

2) 1 кг·м/с

3) 2 кг·м/с

4) 4 кг·м/с

Ре­ше­ние.

Если сила по­сто­ян­на, то им­пульс, пе­ре­дан­ный телу за не­ко­то­рый про­ме­жу­ток вре­ме­ни, равен про­из­ве­де­нию этой силы на время дей­ствия этой силы. Из ри­сун­ка на­хо­дим, что в конце тре­тьей се­кун­ды им­пульс ма­те­ри­аль­ной точки равен

 

Пра­виль­ный ответ ука­зан под но­ме­ром: 4.

Ответ: 4

5955

4

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 14.02.2014 ва­ри­ант ФИ10401.

15. За­да­ние 4 № 6076. Не­боль­шое тело мас­сой 2 кг дви­жет­ся по столу вдоль оси OX. За­ви­си­мость про­ек­ции им­пуль­са p_x этого тела от вре­ме­ни t имеет вид: p_x = 1+2t.

Вы­бе­ри­те вер­ное(-ые) утвер­жде­ние(-ия), если та­ко­вое(-ые) имее(-ю)тся:

А. Тело дви­жет­ся рав­но­уско­рен­но.

Б.В на­чаль­ный мо­мент вре­ме­ни тело имело на­чаль­ную ско­рость 2 м/с.

 

1) толь­ко А

2) толь­ко Б

3) и А, и Б

4) ни А, ни Б

Ре­ше­ние.

Про­ана­ли­зи­ру­ем оба утвер­жде­ния.

Утвер­жде­ние А. Из фор­му­лы видно, что им­пульс растёт ли­ней­но со вре­ме­нем, это озна­ча­ет, что ско­рость также ли­ней­но растёт со вре­ме­нем, то есть дви­же­ние рав­но­уско­рен­ное. Утвер­жде­ние А верно.

Утвер­жде­ние Б. При t = 0 им­пульс тела равен 1 кг·м/с, сле­до­ва­тель­но, ско­рость равна 1/2 = 0,5 м/c. Утвер­жде­ние Б не­вер­но.

 

Пра­виль­ный ответ ука­зан под но­ме­ром: 1.

Ответ: 1

6076

1

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по фи­зи­ке 10.12.2013 ва­ри­ант ФИ10202.

16. За­да­ние 4 № 6812. Телу мас­сой 0,2 кг со­об­щи­ли вер­ти­каль­но на­прав­лен­ную на­чаль­ную ско­рость 10 м/с. Пре­не­бре­гая со­про­тив­ле­ни­ем воз­ду­ха, опре­де­ли­те мо­дуль сред­ней мощ­но­сти силы тя­же­сти, дей­ство­вав­шей на ка­мень во время подъёма до мак­си­маль­ной вы­со­ты. Ответ при­ве­ди­те в Н·м/с.

Ре­ше­ние.

Если на тело, дви­жу­ще­е­ся с по­сто­ян­ной ско­ро­стью дей­ству­ет по­сто­ян­ная сила, то мощ­ность этой силы можно вы­чис­лить как ска­ляр­ное про­из­ве­де­ние силы на ско­рость. По­сколь­ку на тело дей­ству­ет по­сто­ян­ная сила, сила тя­же­сти, а ско­рость убы­ва­ет ли­ней­но, то сред­нюю мощ­ность можно опре­де­лить как по­лу­раз­ность ко­неч­ной и на­чаль­ной мощ­но­стей. При­мем во вни­ма­ние, что в точке наи­выс­ше­го подъёма ско­рость тела равна нулю:

 

Ответ: 10.

Ответ: 10

6812

10

Источник: СтатГрад: Ди­а­гно­сти­че­ская ра­бо­та по фи­зи­ке 12.03.2015 Ва­ри­ант ФИ10901.

17. За­да­ние 4 № 6845. Кусок льда мас­сой 2 кг упал без на­чаль­ной ско­ро­сти на землю с крыши вы­со­той 5 м. Пре­не­бре­гая со­про­тив­ле­ни­ем воз­ду­ха, опре­де­ли­те сред­нюю мощ­ность силы тя­же­сти, дей­ство­вав­шей на тело во время па­де­ния.

Ре­ше­ние.

Найдём ско­рость тела перед па­де­ни­ем, ис­поль­зуя закон со­хра­не­ния энер­гии: от­ку­да Если на тело, дви­жу­ще­е­ся с по­сто­ян­ной ско­ро­стью дей­ству­ет по­сто­ян­ная сила, то мощ­ность этой силы можно вы­чис­лить как ска­ляр­ное про­из­ве­де­ние силы на ско­рость. По­сколь­ку на тело дей­ству­ет по­сто­ян­ная сила, сила тя­же­сти, а ско­рость убы­ва­ет ли­ней­но, то сред­нюю мощ­ность можно опре­де­лить как по­лу­раз­ность ко­неч­ной и на­чаль­ной мощ­но­стей. При­мем во вни­ма­ние, что в на­чаль­ной точке ско­рость тела равна нулю:

 

Ответ: 100.

Ответ: 100

6845

100

Источник: СтатГрад: Ди­а­гно­сти­че­ская ра­бо­та по фи­зи­ке 12.03.2015 Ва­ри­ант ФИ10902.

18. За­да­ние 4 № 6884. Сила при­тя­же­ния Земли к Солн­цу в 22,5 раза боль­ше, чем сила при­тя­же­ния Марса к Солн­цу. Во сколь­ко раз рас­сто­я­ние между Мар­сом и Солн­цем боль­ше рас­сто­я­ния между Землёй и Солн­цем, если масса Земли в 10 раз боль­ше массы Марса?

Ре­ше­ние.

Со­глас­но за­ко­ну все­мир­но­го тя­го­те­ния сила при­тя­же­ния между двумя ма­те­ри­аль­ны­ми точ­ка­ми пря­мо­про­пор­ци­о­наль­на про­из­ве­де­нию их масс и об­рат­но­про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ними.

 

 

Т.о. сила при­тя­же­ния Земли к Солн­цу ,

а сила при­тя­же­ния Марса к Солн­цу .

Чтобы от­ве­тить на во­прос за­да­чи не­об­хо­ди­мо вы­ра­зить от­но­ше­ние

По­лу­ча­ем

Ответ: 1,5

6884

1,5

Источник: ЕГЭ — 2015. До­сроч­ная волна.

19. За­да­ние 4 № 6916. Мо­дуль силы гра­ви­та­ци­он­но­го вза­и­мо­дей­ствия двух то­чеч­ных тел, рас­по­ло­жен­ных на рас­сто­я­нии четырёх мет­ров друг от друга, равен 5 Н. Каков будет мо­дуль силы гра­ви­та­ци­он­но­го вза­и­мо­дей­ствия этих тел, если рас­сто­я­ние между ними уве­ли­чить на 1 м?

Ре­ше­ние.

Со­глас­но за­ко­ну все­мир­но­го тя­го­те­ния сила при­тя­же­ния между двумя ма­те­ри­аль­ны­ми точ­ка­ми пря­мо­про­пор­ци­о­наль­на про­из­ве­де­нию их масс и об­рат­но­про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ними.

 

 

От­но­ше­ние сил гра­ви­та­ци­он­но­го вза­и­мо­дей­ствия в пер­вом и во вто­ром слу­чае . По­лу­ча­ем фор­му­лу для

Ответ: 3,2

6916

3,2

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 14.04.2015 Ва­ри­ант ФИ10601

20. За­да­ние 4 № 6948. Мо­дуль силы гра­ви­та­ци­он­но­го вза­и­мо­дей­ствия двух то­чеч­ных тел, рас­по­ло­жен­ных на рас­сто­я­нии трех мет­ров друг от друга, равен 5 Н. Каков будет мо­дуль силы гра­ви­та­ци­он­но­го вза­и­мо­дей­ствия этих тел, если рас­сто­я­ние между ними умень­шить на 1 м?

Ре­ше­ние.

Со­глас­но за­ко­ну все­мир­но­го тя­го­те­ния сила при­тя­же­ния между двумя ма­те­ри­аль­ны­ми точ­ка­ми пря­мо­про­пор­ци­о­наль­на про­из­ве­де­нию их масс и об­рат­но­про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ними.

 

 

От­но­ше­ние сил гра­ви­та­ци­он­но­го вза­и­мо­дей­ствия в пер­вом и во вто­ром слу­чае . По­лу­ча­ем фор­му­лу для

Ответ: 11,25

6948

11,25

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 14.04.2015 Ва­ри­ант ФИ10602

21. За­да­ние 4 № 7102. Две звез­ды оди­на­ко­вой массы при­тя­ги­ва­ют­ся друг к другу с си­ла­ми, рав­ны­ми по мо­ду­лю F. Во сколь­ко раз умень­шил­ся бы мо­дуль сил при­тя­же­ния между звёздами, если бы рас­сто­я­ние между их цен­тра­ми уве­ли­чи­лось в 1,5 раза, а масса каж­дой звез­ды умень­ши­лась в 2 раза?