7.01. Закон сохранения импульса

Пра­виль­ный ответ: 1.

Ответ: 1

2530

1

44. Че­ло­век мас­сой m пры­га­ет с го­ри­зон­таль­но на­прав­лен­ной ско­ро­стью от­но­си­тель­но Земли из не­по­движ­ной лодки мас­сой М на берег. Если со­про­тив­ле­ние воды дви­же­нию лодки пре­не­бре­жи­мо мало, то ско­рость лодки от­но­си­тель­но Земли в мо­мент от­ры­ва че­ло­ве­ка от лодки равна

 

1)

2)

3)

4)

Ре­ше­ние.

По­сколь­ку со­про­тив­ле­ние воды дви­же­нию лодки пре­не­бре­жи­мо мало, для си­сте­мы че­ло­век-лодка вы­пол­ня­ет­ся закон со­хра­не­ния им­пуль­са. В си­сте­ме от­сче­та, свя­зан­ной с Зем­лей, в про­ек­ции на го­ри­зон­таль­ную ось имеем: , где u — ис­ко­мая ско­рость. Таким об­ра­зом, ско­рость лодки от­но­си­тель­но Земли в мо­мент от­ры­ва че­ло­ве­ка от лодки равна .

Пра­виль­ный ответ: 4.

Ответ: 4

2531

4

45. Ка­мень мас­сой па­да­ет под углом 60° к го­ри­зон­ту со ско­ро­стью 10 м/с в те­леж­ку с пес­ком, по­ко­я­щу­ю­ся на го­ри­зон­таль­ных рель­сах (см. ри­су­нок). Им­пульс те­леж­ки с пес­ком и кам­нем после па­де­ния камня равен

 

1) 40,0 кг м/с

2) 34,6 кг м/с

3) 28,3 кг м/с

4) 20,0 кг м/с

Ре­ше­ние.

По­сколь­ку на си­сте­му в го­ри­зон­таль­ном на­прав­ле­нии не дей­ству­ет ни­ка­ких внеш­них сил, в этом на­прав­ле­нии вы­пол­ня­ет­ся закон со­хра­не­ния им­пуль­са. Пол­ный го­ри­зон­таль­ный им­пульс си­сте­мы до столк­но­ве­ния дол­жен быть равен пол­но­му го­ри­зон­таль­но­му им­пуль­су си­сте­мы после столк­но­ве­ния. Таким об­ра­зом, ис­ко­мый им­пульс те­леж­ки с пес­ком и кам­нем после па­де­ния равен

.

Ответ: 4

3351

4

46. На ри­сун­ке a при­ве­ден гра­фик за­ви­си­мо­сти им­пуль­са тела от вре­ме­ни в инер­ци­аль­ной си­сте­ме от­сче­та. Какой гра­фик  — 1, 2, 3, или 4 (рис. б)  — со­от­вет­ству­ет из­ме­не­нию силы, дей­ству­ю­щей на тело, от вре­ме­ни дви­же­ния?

 

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Им­пульс тела про­пор­ци­о­на­лен его ско­ро­сти. Из гра­фи­ка a видно, что им­пульс ме­ня­ет­ся со вре­ме­нем рав­но­мер­но, сле­до­ва­тель­но, таким же свой­ством об­ла­да­ет и ско­рость тела. Таким об­ра­зом, тело дви­га­ет­ся с по­сто­ян­ным уско­ре­ни­ем. По вто­ро­му за­ко­ну Нью­то­на, уско­ре­ние тела по­сто­ян­но, если по­сто­ян­на дей­ству­ю­ще­го на него сила. От­сю­да за­клю­ча­ем, что пра­виль­ный гра­фик за­ви­си­мо­сти силы от вре­ме­ни изоб­ра­жен на гра­фи­ке 3.

Пра­виль­ный ответ: 3.

Ответ: 3

3474

3

47. Шайба сколь­зит по го­ри­зон­таль­но­му столу и на­ле­та­ет на дру­гую такую же по­ко­я­щу­ю­ся шайбу. На ри­сун­ке стрел­ка­ми по­ка­за­ны ско­ро­сти шайб до и после столк­но­ве­ния. В ре­зуль­та­те столк­но­ве­ния мо­дуль сум­мар­но­го им­пуль­са шайб

 

 

1) уве­ли­чил­ся

2) умень­шил­ся

3) не из­ме­нил­ся

4) стал рав­ным нулю

Ре­ше­ние.

Век­тор им­пуль­са шайбы со­на­прав­лен с век­то­ром ее ско­ро­сти. Ко­эф­фи­ци­ен­том про­пор­ци­о­наль­но­сти яв­ля­ет­ся масса. По­сколь­ку шайбы оди­на­ко­вые, их массы сов­па­да­ют. Сле­до­ва­тель­но, век­то­ра им­пуль­сов шайб до и после столк­но­ве­ния имеют такой же вид, как и век­то­ра ско­ро­стей. Из ри­сун­ка видно, что пол­ный им­пульс при столк­но­ве­нии со­хра­ня­ет­ся, то есть можно сде­лать вывод, что во время со­уда­ре­ния на си­сте­му не дей­ству­ют веш­ние силы. Таким об­ра­зом, мо­дуль сум­мар­но­го им­пуль­са шайб со­хра­ня­ет­ся.

Пра­виль­ный ответ: 3.

Ответ: 3

3581

3

48. Шайба сколь­зит по го­ри­зон­таль­но­му столу и на­ле­та­ет на дру­гую по­ко­я­щу­ю­ся шайбу. На ри­сун­ке стрел­ка­ми по­ка­за­ны им­пуль­сы шайб до и после столк­но­ве­ния. В ре­зуль­та­те столк­но­ве­ния мо­дуль сум­мар­но­го им­пуль­са шайб

 

 

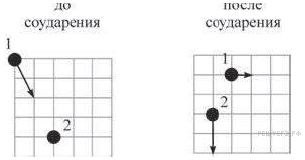
1) уве­ли­чил­ся

2) умень­шил­ся

3) не из­ме­нил­ся

4) стал рав­ным нулю

Ре­ше­ние.

Из ри­сун­ка видно, что им­пульс пер­вой шайбы до столк­но­ве­ния равен сумме век­то­ров им­пуль­сов шайб после столк­но­ве­ния. А зна­чит, мо­дуль сум­мар­но­го им­пуль­са шайб со­хра­ня­ет­ся.

Пра­виль­ный ответ: 3.

Ответ: 3

3597

3

49. Тело дви­жет­ся рав­но­мер­но и пря­мо­ли­ней­но. В не­ко­то­рый мо­мент на тело на­ча­ла дей­ство­вать сила , по­сто­ян­ная по мо­ду­лю и не­из­мен­ная по на­прав­ле­нию. Можно утвер­ждать, что

 

1) век­тор им­пуль­са тела будет все­гда со­на­прав­лен с

2) век­тор из­ме­не­ния им­пуль­са тела будет все­гда со­на­прав­лен с

3) век­тор ско­ро­сти тела будет все­гда со­на­прав­лен с

4) век­тор им­пуль­са тела не будет из­ме­нять сво­е­го на­прав­ле­ния

Ре­ше­ние.

Со­глас­но вто­ро­му за­ко­ну Нью­то­на в им­пульс­ной форме: . То есть на­прав­ле­ни­ем дей­ству­ю­щей на тело силы опре­де­ля­ет­ся толь­ко из­ме­не­ние его им­пуль­са, эти ве­ли­чи­ны со­на­прав­ле­ны. Ско­рость и им­пульс тела могут быть при этом на­прав­ле­ны, как угод­но. На­при­мер, если сила при­ло­же­на к телу пер­пен­ди­ку­ляр­но ско­ро­сти его пер­во­на­чаль­но­го дви­же­ния, то век­тор ско­ро­сти нач­нет по­во­ра­чи­вать­ся под дей­стви­ем силы.

Пра­виль­ный ответ: 2.

Ответ: 2

3628

2

50. Тело дви­жет­ся рав­но­мер­но и пря­мо­ли­ней­но, имея им­пульс . В не­ко­то­рый мо­мент на тело на­ча­ла дей­ство­вать сила , по­сто­ян­ная по мо­ду­лю и не­из­мен­ная по на­прав­ле­нию. В ре­зуль­та­те им­пульс тела из­ме­нил­ся на . Можно утвер­ждать, что

 

1) век­то­ры и со­на­прав­ле­ны

2) век­то­ры и со­на­прав­ле­ны

3) век­то­ры и со­на­прав­ле­ны

4) век­то­ры , и могут быть ори­ен­ти­ро­ва­ны друг от­но­си­тель­но друга про­из­воль­ным об­ра­зом

Ре­ше­ние.

Со­глас­но вто­ро­му за­ко­ну Нью­то­на в им­пульс­ной форме: . То есть век­тор силы и век­тор из­ме­не­ния им­пуль­са со­на­прав­ле­ны. Им­пульс тела может быть при этом на­прав­лен, как угод­но.

Пра­виль­ный ответ: 3.

Ответ: 3

3629

3

51. Мячик мас­сой бро­си­ли с земли вер­ти­каль­но вверх. Через время после брос­ка мячик ока­зал­ся на мак­си­маль­ной вы­со­те. Чему равен мо­дуль из­ме­не­ния им­пуль­са мя­чи­ка за это время? Уско­ре­ние сво­бод­но­го па­де­ния равно . Со­про­тив­ле­ние воз­ду­ха не учи­ты­вать.

 

1)

2)

3)

4)

Ре­ше­ние.

При дви­же­нии мя­чи­ка вер­ти­каль­но вверх на него дей­ству­ет сила тя­же­сти, ко­то­рая со­об­ща­ет ему по­сто­ян­ное уско­ре­ние сво­бод­но­го па­де­ния (по усло­вию, силой со­про­тив­ле­ния воз­ду­ха можно пре­не­бречь). Зна­чит, закон из­ме­не­ния про­ек­ции ско­ро­сти на вер­ти­каль­ную ось, на­прав­лен­ную вверх, имеет вид: , где  —   на­чаль­ная ско­рость мяча (для обо­зна­че­ния вре­ме­ни мы тут ис­поль­зу­ем букву , чтобы от­ли­чать про­из­воль­ный мо­мент вре­ме­ни, для ко­то­ро­го верна вы­пи­сан­ная фор­му­ла, от кон­крет­но­го мо­мен­та вре­ме­ни t, в ко­то­рый мячик ока­зы­ва­ет­ся на мак­си­маль­ной вы­со­те).

 

На мак­си­маль­ной вы­со­те ско­рость об­ра­ща­ет­ся в нуль. От­сю­да мы можем найти ве­ли­чи­ну на­чаль­ной ско­ро­сти: . Сле­до­ва­тель­но, на­чаль­ный им­пульс мя­чи­ка был равен . В точке мак­си­маль­но­го подъ­ема им­пульс, как и ско­рость, об­ра­ща­ет­ся в нуль. Со­от­вет­ствен­но, мо­дуль из­ме­не­ния им­пуль­са мя­чи­ка за время подъ­ема равен .

 

Пра­виль­ный ответ: 3.

Ответ: 3

3702

3

Источник: Яндекс: Тре­ни­ро­воч­ная работа ЕГЭ по физике. Ва­ри­ант 1.

52. Ра­ке­та дви­жет­ся по инер­ции вдали от не­бес­ных тел со ско­ро­стью . Если ре­ак­тив­ный дви­га­тель ра­ке­ты в любой мо­мент вре­ме­ни будет вы­бра­сы­вать про­дук­ты сго­ра­ния топ­ли­ва в на­прав­ле­нии пер­пен­ди­ку­ляр­ном ско­ро­сти (по­ка­за­но на ри­сун­ке жир­ной стрел­кой), то век­тор ско­ро­сти ра­ке­ты

 

1) нач­нет умень­шать­ся по мо­ду­лю, не ме­ня­ясь по на­прав­ле­нию

2) нач­нет уве­ли­чи­вать­ся по мо­ду­лю, не ме­ня­ясь по на­прав­ле­нию

3) нач­нет по­во­ра­чи­вать­ся влево (←), не ме­ня­ясь по мо­ду­лю

4) нач­нет по­во­ра­чи­вать­ся впра­во (→), не ме­ня­ясь по мо­ду­лю

Ре­ше­ние.

Со­глас­но за­ко­ну со­хра­не­ния им­пуль­са, по­сколь­ку топ­ли­во вы­бра­сы­ва­ет­ся ра­ке­той на­пра­во, сама ра­ке­та долж­на по­лу­чать ком­по­нен­ту ско­ро­сти, на­прав­лен­ную на­ле­во. То есть в ре­зуль­та­те ра­бо­ты ре­ак­тив­ных дви­га­те­лей, ра­ке­та будет по­во­ра­чи­вать­ся на­ле­во. Опре­де­лить­ся с тем, что про­ис­хо­дит у мо­ду­лем ско­ро­сти ра­ке­ты, уже не так про­сто. Ко­неч­но, сразу хо­чет­ся ска­зать, что так как топ­ли­во вы­бра­сы­ва­ет­ся пер­пен­ди­ку­ляр­но дви­же­нию ра­ке­ты, то это при­во­дит толь­ко к по­во­ро­ту век­то­ра ско­ро­сти, но не к из­ме­не­нию его ве­ли­чи­ны. И де­таль­ный ана­лиз, ко­то­рый при­ве­ден ниже, дей­стви­тель­но это по­ка­зы­ва­ет. Таким об­ра­зом, верно утвер­жде­ние 3.

 

Пра­виль­ный ответ: 3.

 

Фор­му­ла Ме­щер­ско­го.

Ра­ке­та пред­став­ля­ет собой объ­ект с пе­ре­мен­ной мас­сой, а потом для опи­са­ния ее дви­же­ния нель­зя ис­поль­зо­вать обыч­ную фор­му­ли­ров­ку вто­ро­го за­ко­на Нью­то­на: (в этой фор­му­ле пред­по­ла­га­ет­ся, что масса тела по­сто­ян­на). Вы­ве­дем фор­му­лу, при по­мо­щи ко­то­рой можно опи­сы­вать дви­же­ние тел с пе­ре­мен­ной мас­сой на при­ме­ре ра­ке­ты.

 

Прин­цип дей­ствия ра­ке­ты очень прост. Ра­ке­та с боль­шой ско­ро­стью вы­бра­сы­ва­ет ве­ще­ство (газы), воз­дей­ствуя на него с боль­шой силой. Вы­бра­сы­ва­е­мое ве­ще­ство с той же, но про­ти­во­по­лож­но на­прав­лен­ной силой, в свою оче­редь, дей­ству­ет на ра­ке­ту и со­об­ща­ет ей уско­ре­ние в про­ти­во­по­лож­ном на­прав­ле­нии.

 

Если нет внеш­них сил, то ра­ке­та вме­сте с вы­бро­шен­ным ве­ще­ством яв­ля­ет­ся за­мкну­той си­сте­мой. Им­пульс такой си­сте­мы не может ме­нять­ся во вре­ме­ни. На этом по­ло­же­нии и ос­но­ва­на тео­рия дви­же­ния ракет. Фор­му­лу будем вы­во­дить сле­ду­ю­щим об­ра­зом: при­рав­ня­ем пол­ный им­пульс си­сте­мы в два близ­ких мо­мен­та вре­ме­ни.

 

Пусть  —   масса ра­ке­ты в про­из­воль­ный мо­мент вре­ме­ни , a  —   ее ско­рость в тот же мо­мент. Им­пульс ра­ке­ты в этот мо­мент вре­ме­ни будет . Спу­стя малое время масса и ско­рость ра­ке­ты по­лу­чат при­ра­ще­ния и (ве­ли­чи­на от­ри­ца­тель­на!). Им­пульс ра­ке­ты ста­нет рав­ным . Сюда надо до­ба­вить им­пульс дви­же­ния газов, об­ра­зо­вав­ших­ся за время . Он равен , где — масса газов, об­ра­зо­вав­ших­ся за время , a — их ско­рость. При­рав­ни­вая им­пульс в мо­мен­ты вре­ме­ни и , имеем:

 

По­сколь­ку нас ин­те­ре­су­ет два очень близ­ких мо­мен­та вре­ме­ни можно счи­тать, что все при­ра­ще­ния, малы, а по­то­му, рас­кры­вая скоб­ки, можно от­бро­сить про­из­ве­де­ние , как про­из­ве­де­ние малых. Ввиду со­хра­не­ния массы, . На­ко­нец, вводя ско­рость ис­те­ка­ния газов от­но­си­тель­но ра­ке­ты, , и деля на по­лу­ча­ем окон­ча­тель­ную фор­му­лу:

 

Здесь  —   по сути, ско­рость рас­хо­да топ­ли­ва. Су­ще­ствен­но, что в этом урав­не­нии, в от­ли­чие от при­выч­но­го масса за­ви­сит от вре­ме­ни.

 

Глав­ное, что нужно из этой фор­му­лы для от­ве­та на во­прос, как из­ме­ня­ет­ся ско­рость ра­ке­ты, это тот факт, что век­тор уско­ре­ния ра­ке­ты на­прав­лен про­ти­во­по­лож­но ско­ро­сти ис­те­че­ния про­дук­тов сго­ра­ния топ­ли­ва. Тем самым, в нашем слу­чае, уско­ре­ние ра­ке­ты все время на­прав­ле­но пер­пен­ди­ку­ляр­но ско­ро­сти ра­ке­ты, а зна­чит, это уско­ре­ние при­во­дит толь­ко к по­во­ро­ту век­то­ра ско­ро­сти, но не к из­ме­не­нию его ве­ли­чи­ны (по­доб­но тому, как это про­ис­хо­дит при вра­ще­нии тела по окруж­но­сти).

 

За­ме­ча­ние.

Об­ра­ти­те также вни­ма­ние на то, что для вы­во­да этой фор­му­лы важ­ным эта­пом была воз­мож­ность от­бро­сить сла­га­е­мое , это за­кон­но для слу­чая не­пре­рыв­но­го ис­те­че­ния газов, когда устрем­ляя мы можем сде­лать и из­ме­не­ние массы, и из­ме­не­ние ско­ро­сти сколь угод­но малым. Но это будет не­спра­вед­ли­во, если кто-то вы­ки­ды­ва­ет "кир­пич" из ра­ке­ты, чтобы из­ме­нить ее ско­рость. В ре­зуль­та­те та­ко­го "брос­ка" ско­рость ра­ке­ты из­ме­нит­ся как по ве­ли­чи­не, так и по на­прав­ле­нию.

 

Ответ: 3

3737

3

Источник: Яндекс: Тре­ни­ро­воч­ная работа ЕГЭ по физике. Ва­ри­ант 2.

53. Им­пульс ча­сти­цы до столк­но­ве­ния равен , а после столк­но­ве­ния равен , причём

. Из­ме­не­ние им­пуль­са ча­сти­цы при столк­но­ве­нии рав­ня­ет­ся по мо­ду­лю

 

1)

2)

3)

4)

Ре­ше­ние.

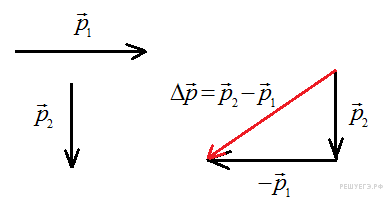Из ри­сун­ка видно, что мо­дуль из­ме­не­ния им­пуль­са ча­сти­цы равен

 

Пра­виль­ный ответ: 1

Ответ: 1

3786

1

Источник: Де­мон­стра­ци­он­ная версия ЕГЭ—2013 по физике.

54. Два тела дви­жут­ся по одной пря­мой. Мо­дуль им­пуль­са пер­во­го тела равен 10 кг м/с, а мо­дуль им­пуль­са вто­ро­го тела равен 4 кг м/с. В не­ко­то­рый мо­мент вре­ме­ни эти тела стал­ки­ва­ют­ся и сли­па­ют­ся. После столк­но­ве­ния мо­дуль им­пуль­са по­лу­чив­ще­го­ся со­став­но­го тела может быть равен

 

1) толь­ко 14 кг м/с

2) толь­ко 6 кг м/с

3) либо 6 кг м/с, либо 14 кг м/с

4) любой ве­ли­чи­не, ле­жа­щей в ин­тер­ва­ле от 6 кг м/с до 14 кг м/с

Ре­ше­ние.

Так как на си­сте­му не дей­ству­ют внеш­ние силы, вы­пол­ня­ет­ся закон со­хра­не­ния им­пуль­са. По­сколь­ку в усло­вии не ска­за­но, дви­га­лись ли два тела до столк­но­ве­ния на встре­чу друг другу или в одном на­прав­ле­нии, не­об­хо­ди­мо рас­смот­реть оба слу­чая.

В пер­вом слу­чае закон со­хра­не­ния им­пуль­са в про­ек­ции на ось, вдоль ко­то­рой дви­га­ют­ся тела, дает:

 

 

В слу­чае же, когда тела дви­га­лись в одном на­прав­ле­нии:

 

 

Таким об­ра­зом, им­пульс по­лу­чив­ше­го­ся со­став­но­го тела может быть равен либо 6 кг м/с, либо 14 кг м/с.

 

Пра­виль­ный ответ: 3.

Ответ: 3

3870

3

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 18.10.2013 ва­ри­ант 1.

55. На по­ко­я­щей­ся те­леж­ке стоит че­ло­век. Масса те­леж­ки , масса че­ло­ве­ка . Че­ло­век на­чи­на­ет рав­но­мер­но дви­гать­ся с од­но­го конца те­леж­ки на дру­гой со ско­ро­стью от­но­си­тель­но те­леж­ки. Мо­дуль ско­ро­сти те­леж­ки от­но­си­тель­но Земли можно вы­чис­лить по фор­му­ле

 

1)

2)

3)

4)

Ре­ше­ние.

На си­сте­му че­ло­век-те­леж­ка в го­ри­зон­таль­ном на­прав­ле­нии не дей­ству­ет ни­ка­ких внеш­них сил. По­это­му для этой си­сте­мы вы­пол­ня­ет­ся закон со­хра­не­ния им­пуль­са. В на­ча­ле им­пульс был равен нулю, таким он и оста­ет­ся все время. Вы­пи­шем закон со­хра­не­ния им­пуль­са, при этом учтем, что ско­рость че­ло­ве­ка от­но­си­тель­но Земли равна , таким об­ра­зом: . От­сю­да сразу на­хо­дим, что мо­дуль ско­ро­сти те­леж­ки от­но­си­тель­но Земли можно вы­чис­лить по фор­му­ле .

Пра­виль­ный ответ: 1.

Ответ: 1

4080

1

Источник: МИОО: Ди­а­гно­стич­ская ра­бо­та по фи­зи­ке 17.12.2012 ва­ри­ант 1.

56.

Два ша­ри­ка оди­на­ко­вой мас­сой m дви­жут­ся с оди­на­ко­вы­ми по мо­ду­лю ско­ро­стя­ми вдоль го­ри­зон­таль­ной плос­ко­сти XY. Из­вест­но, что для си­сте­мы тел, вклю­ча­ю­щей оба ша­ри­ка, про­ек­ция им­пуль­са на ось OY боль­ше нуля, а мо­дуль про­ек­ции им­пуль­са на ось ОХ боль­ше мо­ду­ля про­ек­ции им­пуль­са на ось OY. В этом слу­чае на­прав­ле­ние ско­ро­сти вто­ро­го ша­ри­ка долж­но сов­па­дать с на­прав­ле­ни­ем, обо­зна­чен­ным циф­рой

 

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

Из ри­сун­ка видно, что век­тор им­пуль­са пер­во­го ша­ри­ка имеет ком­по­нен­ты , а че­ты­ре ва­ри­ан­та от­ве­та для век­то­ра им­пуль­са вто­ро­го ша­ри­ка можно за­пи­сать в виде . Сле­до­ва­тель­но, для ком­по­нент пол­но­го им­пуль­са си­сте­мы имеем .

По­сколь­ку, по усло­вию, про­ек­ция пол­но­го им­пуль­са на ось Oy по­ло­жи­тель­на, знак минус для вто­рой ком­по­нен­ты вто­ро­го ша­ри­ка от­па­да­ет, оста­ют­ся ва­ри­ан­ты 1 и 2. Но мо­дуль про­ек­ции им­пуль­са на ось ОХ дол­жен быть боль­ше мо­ду­ля про­ек­ции им­пуль­са на ось OY, а . Сле­до­ва­тель­но, оста­ет­ся толь­ко ва­ри­ант 2.

 

Пра­виль­ный ответ: 2.

Ответ: 2

4115

2

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по фи­зи­ке 05.02.2013 ва­ри­ант 1.

57. Шар сколь­зит по столу и на­ле­та­ет на вто­рой такой же по­ко­я­щий­ся шар. Уче­ни­ки изоб­ра­зи­ли век­то­ры им­пуль­сов шаров до со­уда­ре­ния (верх­няя часть ри­сун­ка) и после него (ниж­няя часть ри­сун­ка). Какой ри­су­нок вы­пол­нен пра­виль­но?