
- •Индивидуальные задания по дисциплине «Математика» для специальностей стр-б-о-141, стрб-б-о-142, стрб-б-о-143
- •1. Вычислить неопределенные интегралы.
- •2. С помощью определенного интеграла вычислить площадь фигуры, ограниченной указанными линиями.
- •3. Найти общие решения (общий интеграл) дифференциальных уравнений первого порядка.
- •4. Найти общие решения линейных неоднородных дифференциальных уравнений второго порядка.
- •5. Изменить порядок интегрирования в повторном интеграле и сделать чертеж области интегрирования.
- •6. Вычислить двойные интегралы, используя полярные координаты.
- •7. Вычислить тройные интегралы.
- •8. Вычислить криволинейные интегралы.
8. Вычислить криволинейные интегралы.
|
№ вар |
Задания |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|

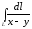 ,
если
,
если
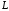 – отрезок прямой
– отрезок прямой
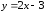 ,
заключенный между точками
,
заключенный между точками
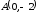 и
и
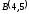 .
.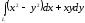 ,
где
,
где
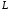 - отрезок прямой
- отрезок прямой
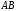 ;
;
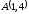 ,
,
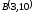 .
.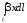 ,
если
,
если
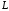 – отрезок дуга параболы
– отрезок дуга параболы
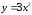 ,
заключенный между точками
,
заключенный между точками
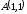 и
и
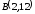 .
.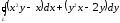 ,
где
,
где
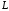 - дуга эллипса
- дуга эллипса
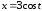 ,
,
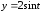 при положительном направлении обхода.
при положительном направлении обхода.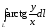 ,
если
,
если
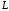 – дуга кардиоиды
– дуга кардиоиды
 ,
,
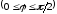 .
.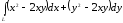 ,
где
,
где
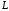 - дуга параболы
- дуга параболы
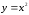 от точки
от точки
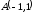 до точки
до точки
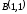 .
.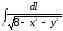 ,
если
,
если
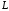 – отрезок прямой, соединяющий точки
– отрезок прямой, соединяющий точки
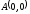 и
и
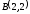 .
.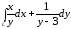 ,
где
,
где
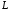 - дуга циклоиды
- дуга циклоиды
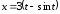 ,
,
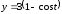 ;
;
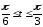 .
.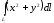 ,
если
,
если
 – верхняя дуга окружности
– верхняя дуга окружности
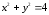 .
.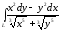 ,
где
,
где
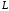 - дуга астроиды
- дуга астроиды
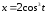 ,
,
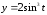 от точки
от точки
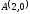 до точки
до точки
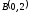 .
.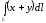 ,
если
,
если
 – дуга лемнискаты Бернулли
– дуга лемнискаты Бернулли
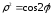 ,
,
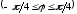 .
.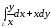 ,
где
,
где
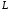 - дуга линии
- дуга линии
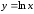 от точки
от точки
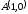 до точки
до точки
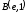 .
.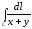 ,
если
,
если
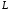 – отрезок прямой
– отрезок прямой
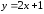 ,
соединяющий точки
,
соединяющий точки
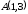 и
и
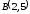 .
.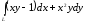 ,
если
,
если
 – дуга эллипса
– дуга эллипса
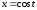 ,
,
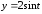 от точки
от точки
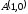 до точки
до точки
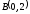 .
.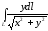 ,
если
,
если
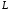 – дуга кардиоиды
– дуга кардиоиды
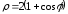 ,
,
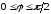 .
.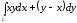 ,
если
,
если
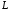 – дуга параболы
– дуга параболы
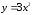 от точки
от точки
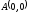 до точки
до точки
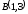 .
.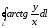 ,
если
,
если
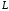 – окружность
– окружность
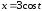 ,
,
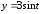 .
.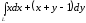 ,
если
,
если
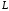 – дуга параболы
– дуга параболы
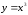 от точки
от точки
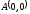 до точки
до точки
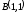 .
.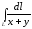 ,
если
,
если
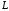 – отрезок прямой
– отрезок прямой
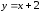 ,
соединяющий точки
,
соединяющий точки
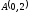 и
и
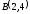 .
.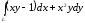 ,
если
,
если
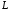 – дуга эллипса
– дуга эллипса
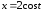 ,
,
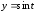 от точки
от точки
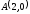 до точки
до точки
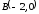 .
.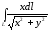 ,
если
,
если
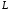 – дуга кардиоиды
– дуга кардиоиды
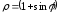 ,
,
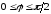 .
.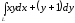 ,
если
,
если
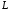 – дуга параболы
– дуга параболы
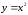 от точки
от точки
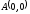 до точки
до точки
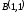 .
.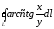 ,
если
,
если
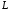 – окружность
– окружность
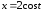 ,
,
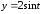 .
.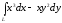 ,
если
,
если
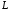 – отрезок прямой, соединяющей точки
– отрезок прямой, соединяющей точки
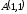 до точки
до точки
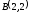 .
.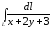 ,
если
,
если
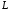 – отрезок прямой
– отрезок прямой
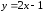 ,
соединяющий точки
,
соединяющий точки
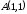 и
и
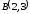 .
.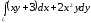 ,
если
,
если
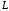 – дуга эллипса
– дуга эллипса
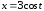 ,
,
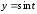 от точки
от точки
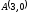 до точки
до точки
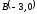 .
.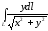 ,
если
,
если
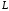 – дуга окружности
– дуга окружности
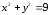 ,
,
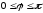 .
.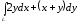 ,
если
,
если
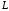 – дуга параболы
– дуга параболы
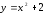 от точки
от точки
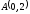 до точки
до точки
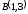 .
.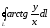 ,
если
,
если
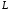 – окружность
– окружность
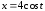 ,
,
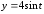 .
.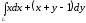 ,
если
,
если
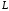 – дуга параболы
– дуга параболы
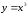 от точки
от точки
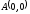 до точки
до точки
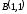 .
.