
Программирование / 4 Программирование вычислительных процессов#
.pdf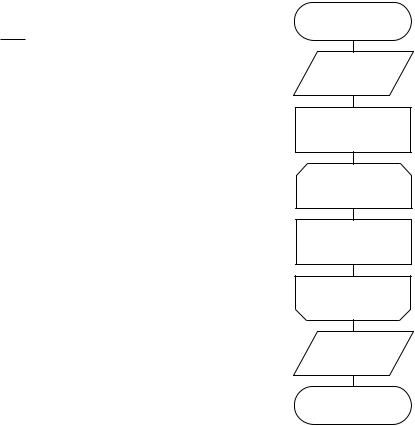
вычисления такого знаменателя в цикле удобно использовать рекуррентную зависимость с памятью в один член последовательности Аi= F(Ai-1). Для вывода рекуррентной формулы следует использовать следующую таблицу.
Номер 1 |
Член последовательности |
Величина |
||||||||
0 |
A0 |
|
1 |
|
|
|||||
1 |
A1 |
|
|
|
|
|
|
X |
2 |
|
9 |
|
|
|
|||||||
|
|
|
|
|||||||
|
|
A0 |
||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
A2 |
|
|
|
|
|
|
X |
2 |
|
7 |
|
|
|
|
||||||
|
|
|
A1 |
|||||||
|
|
|
|
|
|
|
|
|||
3 |
A3 |
|
|
|
|
|
|
X |
2 |
|
5 |
|
|
|
|
|
|||||
|
|
|
A2 |
|||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
4 |
A4 |
|
|
|
|
|
|
X |
2 |
|
3 |
|
|
|
|
|
|
||||
|
|
|
A3 |
|||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
5 |
A5 |
|
|
|
|
|
|
X |
2 |
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
A4 |
|||||||
|
|
|
|
|
|
|
|
|||
Из таблицы видно, что рекуррентная формула принимает вид:
Ai 11 2i X 2 , A0 1,i 1, 2,3, 4,5.
Ai 1
using System; class Example14
{
static void Main()
{
double x, a; Console.WriteLine("Введите x");
x = Convert.ToDouble(Console.ReadLine()); a = 1;
for (int i = 1; i <= 5; i++)
a = 11 - 2 * i - x * x / a; Console.WriteLine("tgx = {0:0.000}", x/a); Console.ReadLine();
}
}
Начало
Ввод x
a:=1
C i:=1; i>5;
a:=11-2i+x*x/a
C i:=i+1
Пример 15.
Пользуясь рекуррентной формулой, для заданного n вычислить
N
SN Yi , известны Y0, Y1, Y2, а Yi (i≥3) вычисляется по формуле:
i 0
Y ln |
Y 2 |
Y |
1 |
. |
i |
i 1 |
i 3 |
|
|
Вывод X/A
Конец
Таблица имен
Математ. |
Обозначение |
Содержательный смысл |
Тип |
величина |
в программе |
|
переменной |
N |
n |
Номер последнего члена последовательности SN |
int |
Y0, Yi-3 |
mem3 |
Член последовательности с номером i-3 |
double |
Y1, Yi-2 |
mem2 |
Член последовательности с номером i-2 |
double |
Y2, Yi-1 |
mem1 |
Член последовательности с номером i-1 |
double |
Yi |
mem |
Член последовательности с номером i |
double |
SN |
summ |
Искомая сумма |
double |
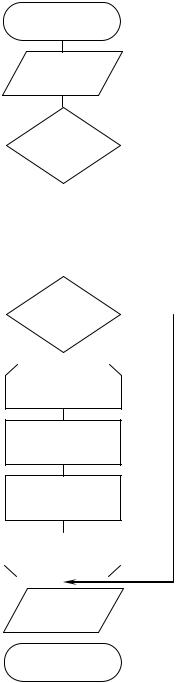
Первым шагом в работе алгоритма является ввод данных Y0, Y1, Y2, N. При вводе трех первых значений последовательности нужно использовать рабочие ячейки mem3, mem2 и mem1 соответственно. На втором шаге требуется проанализировать значение n. Если n < 3, то рекуррентная формула для подсчета summ суммы первых n членов не потребуется. Для определения summ при условии n < 3 в алгоритме предусмотрен переключатель (оператор switch), имеющий три ветви: n = 0, n = 1 и «В противном случае», куда попадает и случай n = 2. Для каждой ветви подсчитывается соответствующая сумма summ. Третий шаг выполняется только в том случае, если n > 2. На этом шаге для i от 3 до n по рекуррентной формуле вычисляются mem, и подсчитывается их сумма summ. Найденное значение summ на последнем четвертом шаге выводится на экран.
using System; class Example15
{
static void Main()
{
double summ, mem, mem1, mem2,
mem3;
Начало
Ввод n, mem3, mem2, mem1
n
0 |
|
1 |
|
|
|
|
|
Иначе |
|||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
summ=mem3 |
|
summ=mem3+ |
|
|
summ=mem3+ |
||||||
|
|
|
|
mem2 |
|
|
mem2+mem1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
False |
|
|
|
|
|
n > 2 |
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
True |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
C i=3; i>n;
mem:=Math.Log(Math.Abs
(mem1*mem1+mem3+1));
summ:=summ+mem;
mem3=mem2;
mem2=mem1;
mem1:=mem;
int n; |
|
|
|
|
|
C |
|||
Console.WriteLine("Введите первые |
|
|||
|
i=i+1 |
|||
три члена последовательности"); |
|
|||
|
|
|
|
|
|
|
|
|
|
mem1 = |
|
|
|
|
|
|
|
|
|
Convert.ToDouble(Console.ReadLine()); |
|
Вывод summ |
||
mem2 = |
|
|||
|
|
|
|
|
Convert.ToDouble(Console.ReadLine()); |
|
|
|
|
mem3 = |
|
|
|
|
|
|
|
|
|
Convert.ToDouble(Console.ReadLine()); |
|
Конец |
||
Console.WriteLine("Введите номер |
|
|||
|
|
|
|
|
последнего учитываемого члена |
|
|
|
|
последовательности"); |
|
|
|
|
n = Convert.ToInt32(Console.ReadLine()); |
|
|
|
|
switch (n) |
|
|
|
|
{ |
|
|
|
|
case 0: |
|
|
|
|
summ = mem3; |
|
|
|
|
break; |
|
|
|
|
case 1: |
|
|
|
|
summ = mem3 + mem2; |
|
|
|
|
break; |
|
|
|
|
default: |
|
|
|
|
summ = mem3 + mem2 + mem1; |
|
|
|
|
break; |
|
|
|
|
} |
|
|
|
|
if (n>2) |
|
|
|
|
for (int i = 3; i <= n; i++) |
|
|
|
|
{ |
|
|
|
|
mem = Math.Log(Math.Abs(mem1 * mem1 + mem3 + 1)); |
||||
summ += mem; |
|
|
|
|
mem3 = mem2; mem2 = mem1;
mem1 = mem;
}
Console.WriteLine("S= {0:0.000}", summ); Console.ReadLine();
}
}
Пример 16. Вычислить с точностью ε квадратный корень из величины X, Y 
 X .
X .
Вычисление проводить по рекуррентной формуле: Yi 0.5(Yi 1 X ), выбрав в качестве начального
Yi 1
X , X 1
приближения величину Y .
0 0.5X , X 1
При решении подобных задач условие остановки вычислительного процесса формулируется следующим образом: |Yi — Yi-1 |<ε.
Математ. |
Обозначение |
Содержательный смысл |
Тип |
|
величина |
в программе |
переменной |
||
|
||||
i |
i |
Номер итерации |
int |
|
Yi-1 |
prevmemb |
Член послед. У с номером i-1 |
double |
|
Yi |
memb |
Член последовательности У с номером i |
double |
|
X |
x |
Величина X, квадратный корень которой мы ищем |
double |
|
ε |
accuracy |
Требуемая точность расчетов |
double |
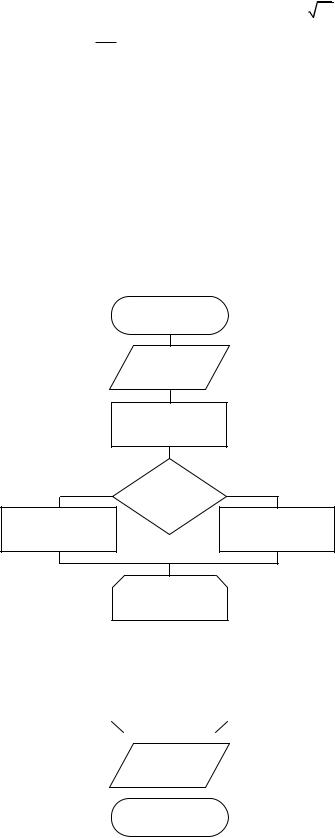
Вводим с клавиатуры величины x и accuracy. Далее вычисляем первое приближение memb. Если x<1, то memb принимается равным x, в противном случае за memb принимается величина x/2. Далее на основании memb нужно найти следующее приближение. Поэтому вычисленное значение записывается в ячейку с именем prevmemb и с этого момента времени считается предыдущим значением. Текущее значение memb рассчитывается по рекуррентной формуле на основании prevmemb и x. Этот циклический процесс повторяется до тех пор, пока не выполнится условие |memb – prevmemb| < acuracy. После чего memb считается равным значению корня из x с точностью accuracy и выводится на экран монитора.
|
Начало |
|
Ввод x, |
|
accuracy |
|
memb=x; |
False |
True |
|
x>=1 |
memb=x/2; |
memb=x/2; |
|
A |
|
memb |
|
|
|
|
|
|
|
using System; |
|
|
prevmemb=memb; |
|||
|
|
memb=(prevmemb+ |
||||
class Example16 |
|
|
x/prevmemb)/2; |
|||
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
static void Main() |
|
|
|
|
|
|
|
|
A |
|
|||
{ |
|
|
Math.Abs(memb- |
|
||
double memb, prevmemb, accuracy, x; |
|
prevmemb)>accyracy |
|
|||
|
|
|||||
Console.WriteLine("Введите x и |
|
|
|
|
|
|
|
|
|
|
|
|
|
точность"); |
|
|
Вывод |
|||
x = |
|
|
memb |
|||
Convert.ToDouble(Console.ReadLine()); |
|
|
||||
|
|
|
|
|
|
|
accuracy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
Convert.ToDouble(Console.ReadLine()); |
|
|
Конец |
|||
memb = (x >= 1) ? x : (x / 2); |
|
|
||||
|
|
|
|
|
|
|
do |
|
|
|
|
|
|
{ |
|
|
|
|
|
|
prevmemb = memb; |
|
|
|
|
|
|
memb = (prevmemb + x / prevmemb) / 2; |
|
|
|
|
|
|
} while (Math.Abs(memb - prevmemb) > accuracy); Console.WriteLine("y= {0:0.0000}", memb); Console.ReadLine();
}
}
4.4.12. Вычисление предела последовательности
Вычисление предела последовательности является типичной задачей на использование итерационного цикла.
Пример 17. Последовательность {Xn} определена следующим образом:
|
|
|
n2 2 |
|
|
|
|
|
X n |
|
, n 1, 2,3... |
|
|
|
|
3n2 n 1 |
|
|
||
Найти предел последовательности {Xn}, принимая за него такое Хn, при котором |
||||||
|
|
|
|Xn – Xn-1| < ε. |
|
|
|
|
|
|
|
|
Таблица имен |
|
Математ. |
Обозначение |
Содержательный смысл |
Тип |
|
||
величина |
в программе |
|
|
|
переменной |
|
|
|
|
|
|
|
|
n |
n |
|
Номер итерации |
int |
|
|
Xn-1 |
prevmemb |
Член последовательности X с номером n-1 |
double |
|
||
Хn |
memb |
Член последовательности X с номером n |
double |
|
||
ε |
accuracy |
Требуемая точность расчетов |
double |
|
||
using System; class Example17
{
static void Main()
{
double memb, prevmemb, accuracy; int n;
Console.WriteLine("Введите точность");
accuracy = Convert.ToDouble(Console.ReadLine()); memb = 1;
n = 1; do
{
prevmemb = memb;
memb = (double) (n * n + 2) / (3 * n * n - n + 1); n++;
} while (Math.Abs(memb - prevmemb) < accuracy);
Console.WriteLine("Предел последовательности равен {0:0.00000}", memb); Console.ReadLine();
}
}
4.4.13. Вычисление суммы бесконечного ряда с использованием рекуррентной формулы
Для вычисления на компьютере сумм бесконечного ряда часто используют рекуррентные формулы, с помощью которых друг за другом вычисляют значения членов бесконечной последовательности. Рекуррентные формулы существенно сокращают время работы программы, упрощают процесс написания программы и ее отладки. Как правило, рекуррентные формулы программист должен составить сам. В этом и состоит искусство программирования вычислительных процессов. Рекуррентная формула может и отсутствовать. В этом случае каждый член ряда придется рассчитывать «в лоб» по полной формуле.
Есть определенные признаки, которые помогают выявить наличие рекуррентных формул. К таким признакам относятся выражения (-1)n, Xn, n! и подобные этим выражения, присутствующие в формуле общего члена бесконечного ряда. Часто рекуррентная формула для бесконечного ряда находится путем деления соседних членов ряда друг на друга.

|
|
|
|
|
|
X |
2i |
|
||
Пример 18. Вычислить Y ( 1)i |
|
|
. Вычисление ряда окончить при выполнении |
|||||||
(2i)! |
||||||||||
|
|
|
|
|
i 1 |
|
||||
|
|
|
|
|
|
|
|
|
||
условия: |
|
X 2i |
|
. |
|
|
|
|
||
|
|
|
|
|
|
|||||
|
(2i)! |
|
|
|
|
|
|
|||
Для решения этой задачи необходимо использовать рекуррентную формулу. А найти ее можно следующим способом. Сделаем преобразование исходного ряда в следующий вид:
YAi , Ai ( 1)i X 2i i 1 (2i)!
Тогда условие окончания вычислений будет выглядеть так | Ai | < ε. Это условие либо выполнится, для некоторого i = n и вычислительный процесс будет завершен, либо не выполнится. Во втором случае используют термин «зависание программы». Программист искусственно останавливает программу и выясняет причину зависания: неправильные исходные данные, например комбинация X и ε, или допущена ошибка в тексте программы, а может быть получена неправильная рекуррентная формула, или другая причина имеет место.
Нас в этом примере интересует нормальный режим работы программы, а это означает, что существует такое n, для которого справедливы следующие формулы:
n |
X |
2i |
|
||
Y Ai , Ai ( 1)i |
|
|
,| Ai | . |
||
(2i)! |
|||||
i 1 |
|
||||
|
|
|
|
||
Эти формулы и будут исходными для нашей задачи. На этом первый этап подготовки бесконечного ряда к нахождению его суммы Y с погрешностью ε на компьютере завершается. Если рекуррентную формулу найти невозможно или нет в этом необходимости, то можно ограничиться только приведенными выше преобразованиями.
Но в нашем случае нужен второй этап преобразования, а именно, нахождение рекуррентной формулы. Для этого поделим два соседних члена Аi, Аi-1 (Иногда, с точки зрения математических преобразований проще будет разделить Аi+1 на Аi, что эквивалентно):
|
|
( 1)i |
X 2i |
|
|
|
X 2i |
|
|
|
X 2i |
|
|
|
|||||
A |
|
(2i)! |
|
|
(2i)! |
|
(2i 2)! (2i 1) (2i) |
|
X 2 |
||||||||||
|
|
|
|
|
|||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
X 2(i 1) |
X 2i 2 |
|
X 2i X 2 |
|
||||||||||
A |
|
( 1) |
i 1 |
|
|
|
|
|
|
(2i) (2i 1) |
|||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(2(i 1))! |
|
|
(2i 2)! |
|
|
(2i 2)! |
|
|
|
|||||||
Отсюда находим рекуррентную формулу:
Ai (2i) (2i 1) ,i 2,3,..., n.
Осталось только определить первый член ряда. Для этого, в формулу Ai вместо i подставим 1:
|
|
A ( 1)1 |
|
X 2 1 |
|
X |
2 |
|
X 2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
(2 1)! |
|
2! |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица имен |
|
Математ. |
Обозначение |
Содержательный смысл |
|
|
Тип |
|
|||||||
величина |
в программе |
|
|
|
|
|
|
|
|
|
|
переменной |
|
i |
i |
Номер итерации |
|
|
|
|
|
|
|
|
|
int |
|
X |
x |
Параметр бесконечного ряда |
|
|
|
|
double |
|
|||||
Y |
summ |
Искомая сумма |
|
|
|
|
|
|
|
|
|
double |
|
Ai |
memb |
Член последовательности А с номером i |
double |
|
|||||||||
ε |
accuracy |
Требуемая точность расчетов |
|
|
double |
|
|||||||
using System; class Example18
{
static void Main()
{
double summ, memb, x, accuracy; int i;
Console.WriteLine("Введите точность");

accuracy = Convert.ToDouble(Console.ReadLine()); Console.WriteLine("Введите x");
x = Convert.ToDouble(Console.ReadLine()); memb = -x * x / 2;
i = 1;
summ = memb;
while (Math.Abs(memb) >= accuracy)
{
i++;
memb = (double)-x * x / (4 * i * i - 2 * i);
}
Console.WriteLine("Сумма ряда равна {0}\nУчтено {1} элементов", memb, i); Console.ReadLine();
}
}
4.4.14. Примеры вложенных цикл
Под вложенным циклом понимают такую алгоритмическую структуру,
при которой в тело одного цикла с параметром включен другой цикл со своим |
|
Начало |
|||||
параметром. |
|
|
|
||||
|
|
|
|
|
|
||
10 |
15 |
|
|
|
|
|
|
Пример 19. Вычислить S k3 |
(k p)2 |
|
summ_k=0; |
||||
k 1 |
p 1 |
|
|
|
|
||
Для решения этой задачи необходима дополнительная переменная, как |
|
|
|
|
|||
|
|
|
|
||||
иногда говорят, рабочая ячейка R (переменная summ_p) для накопления в |
|
|
|
|
|||
|
A |
||||||
процессе вычисления S (переменная summ_k) вложенной суммы: |
|
k=1; |
|||||
|
k>10; |
||||||
|
15 |
|
|
||||
|
|
|
|
|
|
||
R (k p)2 |
|
|
|
|
|||
|
summ_p=0; |
||||||
|
p 1 |
|
|||||
|
|
|
|
||||
using System; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
class Example19 |
|
|
|
B |
|||
{ |
|
|
|
p=1; |
|||
static void Main() |
|
|
|
p>15; |
|||
{ |
|
|
|
|
|
|
|
double summ_k, summ_p; |
|
|
|
summ_p= |
|||
summ_k = 0; |
|
|
|
summ_p+(k-p)2; |
|||
for (int k = 1; k <= 15; k++) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
B |
||||
{ |
|
|
|
||||
|
|
|
p++ |
||||
summ_p = 0; |
|
|
|
||||
|
|
|
|
|
|
||
for (int p = 1; p <= 15; p++) |
|
|
|
|
|||
|
|
|
|
||||
summ_p += (k - p) * (k - p); |
|
|
|
|
|||
summ_k=summ_k+ |
|||||||
summ_k += k * k * k * summ_p; |
|||||||
|
k3*summ_p; |
||||||
} |
|
|
|
||||
|
|
|
|
|
|
||
Console.WriteLine("S= {0}", summ_k); |
|
|
|
|
|
||
|
|
|
|
|
|||
|
|
A |
|||||
Console.ReadLine(); |
|
|
|
k++ |
|||
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Во-первых, теоретически возхможно сделать так, чтобы все вложенные циклы управлялись одной и той же переменной, однако это затрудняет понимание и отладку программы. На практике старайтесь для каждого вложенного цикла объявлять свою уникальную переменную, которая будет управлять его работой.
Во-вторых, здесь не использована возможность цикла for – использовать несколько переменных в разделах инициализации и итерации. Так, переменные, накапливающие суммы, можно тоже инициализировать и накапливать в них сумму в соответствующих разделах:
using System;
class Example19_shoter
{
static void Main()
{
double summ_k=0;
for (int k = 1, summ_p = 0; k <= 15;summ_k += k * k * k * summ_p, k++, summ_p=0) for (int p = 1; p <= 15; summ_p += (k - p) * (k - p), p++);
Console.WriteLine("S= {0}", summ_k); Console.ReadLine();
}
}
Как видно, данный код программы является более лаконичным и, вместе с тем, более трудным для понимания (такова цена лаконичности). Рассмотрим его более подробно. Вне циклов объявлена только одна переменная summ_k, поскольку вывод ее значения осуществляется тоже вне циклов. Если бы она была объявлена в инициализирующей части цикла for по k, то вне его доступ к ней получить было бы не возможно.
Управляющие переменные (k и p) инициализируются внутри операторов for (как и в предыдущем случае). Однако во внешнем цикле инициалищируется и переменная summ_p, поскольку вне его она не нужна. Внутренний цикл – без тела. Накапливание суммы происходит в итерационной части оператора. Обратите внимание на порядок следования операторов – сначала происходит увеличение переменной summ_p, а затем переменная p инкрементируется. При
обратном порядке потерялся бы первый элемент суммы. |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Вренемся к внешнему циклу. В итерационной |
||||||||||
|
|
Начало |
|
|
|
|
|
|
|
|
|
части оператора for выполняется 3 действия: |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
сначала |
накапливается |
искомая |
сумма |
в |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
переменную |
summ_k, |
затем |
увеличение |
k, и |
в |
|||||
|
lucky_ticket=-1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
завершение |
– |
обнуление |
|
переменной |
summ_p. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
F |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Последнее действие необходимо, поскольку после |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
digit5++ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
A |
|
|
|
|
|
|
|
|
|
завершения работы внутреннего цикла переменная |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
digit0=0; |
|
|
|
|
|
|
|
|
|
summ_p |
будет |
содержать |
|
некоторое |
значение, |
||||||
|
|
digit0>10; |
|
|
|
|
|
|
E |
|
|||||||||||||
|
|
|
|
|
|
|
|
которое |
для |
нахождения суммы при |
следующем |
||||||||||||
|
|
|
|
|
|
|
|
|
|
digit4++ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
B |
|
|
|
|
|
|
|
|
|
значении |
k |
должно |
быть |
удалено (в |
противном |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
digit1=0; |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
случае в summ_p для каждого k, будет включаться |
||||||||||||
|
|
digit1>10; |
|
|
|
|
|
|
D |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
digit3++ |
значение summ_p для k-1). |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
digit2=0; |
|
|
|
|
|
|
|
|
|
Пример 20. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
digit2>10; |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
digit2++ |
Используя вложенный цикл, определить число |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
D |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
счастливых билетов lucky_ticket, номера которых |
||||||||||||
|
|
digit3=0; |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
digit3>10; |
|
|
|
|
|
|
B |
меняются от 000001 до 999999. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
digit1++ |
В |
основе |
алгоритма |
решения этой |
задачи |
||||||||
|
|
E |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
лежит |
принцип |
десятичного |
счетчика, |
имеющего |
||||||||
|
|
digit4=0; |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
digit4>10; |
|
|
|
|
|
|
A |
шесть разрядов. |
Роль разрядов играют индексы в |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
digit0++ |
следующем порядке digit0, digit1, digit2, digit3, |
||||||||||||
|
|
F |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
digit5=0; |
|
|
|
|
|
|
|
|
|
digit4, digit5. Счастливым называется такой номер, у |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
digit5>10; |
|
|
|
|
|
|
Вывод |
которого три левых разряда в сумме равны сумме |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
lucky_ticket |
трех правых разрядов. |
|
|
|
|
|
|
||||||
|
digit0+digit1+digit2= |
FALSE |
|
|
|
|
|
В связи с тем, что номер 000000 в катушке |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
билетов отсутствует, то этот номер нужно вычесть |
|||||||||||||
|
=digit3+digit4+digit5 |
|
|
|
|
|
|
Конец |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
TRUE |
|
|
|
|
|
|
из найденного числа. Это можно сделать разными |
|||||||||||||
|
|
|
|
|
|
|
|
|
способами. В предложенном алгоритме это |
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
lucky_ticket+=1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
реализовано |
через |
инициализацию |
переменной |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
lucky_ticket значеним -1. Это решение логично. При |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
исходном |
|
состоянии |
счетчика |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
digit0=digit1=digit2=digit3=digit4=digit5=0, |
условие |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
digit0+digit1+digit2==digit3+digit4+digit5 принимает значение TRUE, и lucky_ticket увеличивается на 1 и становится равным нулю lucky_ticket = -1 + 1 = 0. Таким образом, все переменные приняли исходное значение для дальнейших расчетов.
using System; class Example20
{
static void Main()
{
double lucky_ticket=0;
for (int digit0 = 0; digit0 < 10; digit0++)
for (int digit1 = 0; digit1 < 10; digit1++)
for (int digit2 = 0; digit2 < 10; digit2++)
for (int digit3 = 0; digit3 < 10; digit3++)
for (int digit4 = 0; digit4 < 10; digit4++)
for (int digit5 = 0; digit5 < 10; digit5++)
lucky_ticket += (digit0 + digit1 + digit2 == digit3 + digit4 +
digit5) ? 1 : 0;
Console.WriteLine("Число счастливых билетов= {0}", lucky_ticket); Console.ReadLine();
}
}
Для проверки и увеличения переменной lucky_ticket используется составной оператор присваивания += и оператор ?. То есть, если условие (digit0 + digit1 + digit2 == digit3 + digit4 + digit5) выполняется, то к переменной lucky_ticket прибавляется 1, в противном случае – прибавляется 0.
Основным достоинством вложенного цикла является возможность в выражениях (в заголовке цикла или его теле) использовать параметры внешних циклов. Например, в описанном выше примере, в теле цикла с параметром digit5 используются также текущие значения параметров digit0 , digit1 , digit2 , digit3 ,digit4 внешних циклов по отношению к этому циклу.
Допускается выход из тела цикла любого уровня вложения на любой предыдущий уровень до полного завершения цикла с помощью оператора goto.
Пример 21.
Составить программу для нахождения числа слов в предложении и количества букв в самом длинном слове.
Решение этой задачи сделаем в предположении: в конце предложения стоит точка, слова не имеют знака переноса и написаны на русском языке. В теле предложения могут стоять знаки препинания, но после каждого из них должен быть один пробел, который для предлагаемой программы является разделителем слов. Переменные, используемые в программе, и их тип описаны в следующей таблице.
Идентификатор |
Содержательный смысл |
Тип переменной |
ch_count |
Число букв в новом слове |
int |
maxch_count |
Число букв в самом длинном слове |
int |
words_count |
Число слов |
int |
ch |
Последний символ, введенный с клавиатуры |
char |
В программе используется три счетчика ch_count, maxch_count, words_count и переменная ch для чтения из стандартного входного потока текущего символа (литеры). Алгоритм содержит два итерационных цикла. Внешний цикл с постусловием используется для подсчета числа слов в предложении words_count, а также для выявления самого длинного слова (формирование значения переменной maxch_count). Внутренний цикл обеспечивает чтение очередной литеры ch, отделяет русские буквы от знаков препинания и латинских букв, определяет конец слова и подсчитывает количество букв ch_count в текущем слове. Концом слова считается пробел или точка.
using System; class Example21
{
static void Main()
{
int ch_count, maxch_count, words_count; double ch;
Console.WriteLine("Введите слова, разделенные пробелами"); Console.WriteLine("В конце предложения поставьте точку"); maxch_count = words_count =0;
do
{
ch_count = 0; ch = '*';
while ((ch != ' ') && (ch != ',') && (ch != '.')) //Конец слова
{
ch = Console.Read();
if ((('А' <= ch) && (ch <= 'Я')) || ((('а' <= ch) && (ch <= 'п')) || (('р' <= ch) && (ch <= 'я'))))
ch_count++;
}
words_count += (ch == ',') ? 0 : 1;
if (maxch_count < ch_count) maxch_count = ch_count;
}
while (ch != '.'); Console.ReadLine(); Console.WriteLine(maxch_count); Console.WriteLine(words_count); Console.ReadLine();
}
}
