135

«Эконометрика» Тесты

1. Какие переменные называются предопределенными:

а) экзогенные;

б) эндогенные;

в) лаговые;

г) экзогенные и лаговые.

2.1.1 Перепись населения является

а) выборочным исследованием;

б) сбором данных о генеральной совокупности;

в) выборкой.

2.1.2. По некоторой выборке нельзя судить о генеральной совокупности. В таком случае говорят, что выборка

а) не нормализована;

б) не структурирована;

в) не репрезентативна;

г) не показательна.

2.2.1 Чему равен размах выборки {1, 30, 1000, 24, 99 }?

а) 98

б) 999

в) 1000

г) 230,8

2.2.2 Какова сумма абсолютных частот в следующей выборке {25, 30, 42, 30, 30, 42, 25}?

а) 7

б) 3

в) 97

г) 1

2.2.3 Какова сумма относительных частот в выборке {5, 3, 2, 3, 5, 2, 5, 2, 3}

а) 9

б) 1

в) 10

г) 30

2.2.4 По формуле , где N_k - число опытов, в которых произошло событие А_k при полном числе испытаний N, определяется:

а) относительная частота появления события А_k

б) интегральная частота появления события А_k

в) размах выборки появления события А_k

г) репрезентативность появления события А_k

2.2.5 В выборке {5, 3, 2, 3, 5, 2, 5, 2, 3, 2} интегральная относительная частота _z=2 равна:

а) 2

б) 0,3

в) 0,4

г) 3

2.2.6. В выборке {5, 3, 2, 3, 5, 2, 5, 2, 3, 3} интегральная относительная частота  _z=3 равна:

а) 5

б) 0,4

в) 0,7

г) 2

7. Чему равна относительная частота _k для k=2 в выборке {5, 3, 2, 3, 5}

а) 3

б) 1

в) 5

г) 0,4

2.2.8 Статистическим распре­делением выборки называют

а) последовательность пар различных элементов выборки и их относительных частот

б) последовательность пар различных элементов выборки и их абсолютных частот

в) значения накопленных частот

г) кусочно-постоянную неубывающую функцию, изменяющуюся от 0 до 1.

2.3.1 Чему равен размах выборки {1, 5, 12, 1, 5, 12, 1, 5}

а) 3

б) 11

в) 4

г) 8.

2.3.2. Плотность вероятности f(x) можно интерпретировать как

а) вероятность попадания реализации случайной величины Х в бесконечно малый интервал, в расчете на единицу его длины;

б) вероятность того, что случайная величина Х попадает в интервал, содержащий точку х, в расчете на единицу его длины;

в) вероятность попадания реализации случайной величины Х в бесконечно малый интервал, содержащий точку х, в расчете на единицу его длины;

г) вероятность того, что случайная величина Х принимает значение меньше данного числа х;

2.3.2. Функция распределения F_Х(x) случайной величины Х можно интерпретировать как

а) вероятность попадания реализации случайной величины Х в бесконечно малый интервал, в расчете на единицу его длины;

б) вероятность того, что случайная величина Х попадает в интервал, содержащий точку х;

в) вероятность того, что случайная величина Х принимает значение не более данного числа х;

г) вероятность того, что случайная величина Х принимает значение меньше данного числа х;

2.3.4. В анализе непрерывных случайных величин относительные частоты являются

а) величинами, зависящими от размаха выборки;

б) величинами, не зависящими от размаха выборки и выбранного количества интервалов для группировки;

в) величинами, зависящими от размаха выборки и выбранного количества интервалов для группировки;

г) величинами, зависящими от выбранного количества интервалов для группировки;

2.4.1 Чему равно математическое ожидание числа, которое выпадает при подбрасывании игральной кости?

а) 3

б) 3,5

в) 1,2,3,4,5,6

г) 21

2.4.2 Известно, что математическое ожидание M[Х] некоторой случайной величины Х равно 40, а M[Х²] = 1990. Чему равна дисперсия?

а) 1170

б) 1462500

в) 390

г) 1600

2.4.3 В некоторой выборке дисперсия доходов населения в неденоминированных рублях (до 1.01.1998) года составила 439560000000 рублей². Чему она равна в деноминированных рублях.

а) 439560 руб.²

б) 439560000 руб.²

в) 66299,32 руб.²

г) 439560 тыс. руб.²

3.1.1. Чему равен парный коэффициент корреляции для переменных, зависимость между которыми отображена на графике?

а) r_ху =1

б) r_ху =0

в) r_ху = -1

г) r_ху = 0,5

3.1.2. Коэффициент корреляции r_ху может принимать значения только в пределах:

а) -1r_ху 1

б) 0r_ху 1

в) –1<r_ху <1

г) 0r_ху <1

3.1.3. Спрос на белый хлеб (y) зависит от цен на белый (x1) и черный хлеб (x2). Какое утверждение верно?

а) 0<r _yx1<1 б) r _yx2 =0 в) -1<r _yx1 < 0 г) r_yx2 < r_yx1

3.1.4. Спрос на белый хлеб (y) зависит от цен на белый (x1) и черный хлеб (x2). Что можно сказать о коэффициенте корреляции r_yx1?

а) r _yx1<1

б) r _yx1 >0

в) r _yx1 > -1

г) r _yx1 < 0

3.2.1. Деятельность n=6 карьеров характеризуется себестоимостью 1т песка (х1), объемом добычи песка за смену (х2) и фондоотдачей (х3). Оценены парные коэффициенты корреляции r₁₂=0,8 ; r₂₃= 0,6; r₁₃= 0,7; По таблице функции распределения Стьюдента для двусторонней критической области определите определите, какие из коэффициентов корреляции значимы при =0,1

	0,005	0,01	0,025	0,05	0,1
1	127,3211	63,6559	25,45188	12,70615	6,313749
4	5,59754	4,60408	3,495406	2,776451	2,131846
6	4,316826	3,707428	2,968682	2,446914	1,943181
8	3,832538	3,355381	2,751531	2,306006	1,859548

а) r₁₂ и r₂₃

б) r₁₂, r₂₃ и r₁₃

в) r₁₂

г) r₁₂ и r₁₃

3.2.2. Для оценки значимости парного коэффициента корреляции используется

а) t-статистика, рассчитываемая по формуле и  = n-2.

б) F-статистика с параметрами ₁=n и ₂=r

в) t-статистика, рассчитываемая по формуле t = r и  = n-2.

г) F-статистика с параметрами ₁=n-2 и ₂=n.

1. При оценке линейной зависимости переменных методом наименьших квадратов в качестве критерия близости используется

а) минимум суммы модулей разностей наблюдений зависимой переменной y_i и теоретических, рассчитанных по уравнению регрессии значений (a+bx)

б) минимум квадратов разностей наблюдений зависимой переменной y_i и теоретических, рассчитанных по уравнению регрессии значений (a+bx)

в) минимум суммы квадратов разностей наблюдений зависимой переменной y_i и теоретических, рассчитанных по уравнению регрессии значений (a+bx)

г) минимум суммы разностей наблюдений зависимой переменной y_i и теоретических, рассчитанных по уравнению регрессии значений (a+bx)

2. Какие требования в модели регрессионного анализа предъявляются к распределению ошибок наблюдения _i , а именно к их математическому ожиданию M[_i]и дисперсии D[_i ]:

а) M[_i]=1; D[_i ]=²

б) M[_i]=0; D[_i ]=1

в) M[_i]=0; D[_i ]=²

г) M[_i]=1; D[_i ]=0

3.3.3. Наблюдения 16 пар (X,Y) дали следующие результаты: Y²=526, Y=64, X²=657, X=96, XY=492. Чему равен коэффициент b в уравнении регрессии: Y_i=a+bX_i+e_i

а) 0,77

б) 1,33

в) 1

г) 0,7

4. По результатам бюджетного обследования случайно выбранных семей построено уравнение регрессии зависимости накоплений S от доходаY:

S_i= -33,5+1,05Y_i+e_i

Спрогнозируйте накопления семьи, имеющей доход 40 тыс. руб.

а) 42

б) 8,5

в) 4,2

г) 1,05

4. По результатам бюджетного обследования случайно выбранных семей построено уравнение регрессии зависимости накоплений S от дохода Y:

S_i= -33,5+1,05Y_i+e_i

Как изменятся накопления, если доходы увеличатся на 10 тыс. руб.?

а) возрастут на 1,05 тыс.руб.

б) уменьшатся на 33,5 тыс. руб.

в) возрастут на 10,5 тыс. руб.

г) данных недостаточно

4. По результатам бюджетного обследования случайно выбранных семей построено уравнение регрессии зависимости накоплений S от дохода Y:

S_i= -33,5+1,05Y_i+e_i

Начиная с какого уровня дохода это уравнение имеет экономический смысл?

а) 1,05 тыс. руб.

б) 40,05 тыс. руб.

в) 31,91 тыс. руб.

г) 32,00 тыс. руб.

3.4.1. По выборке из 20 наблюдений была оценена парная регрессия y=f(x). Для коэффициента регрессии а₁ получена t-статистика: t₁= -2,09. По таблице функции распределения Стьюдента для двусторонней критической области определите, на каком максимальном уровне значим полученный коэффициент.

 / 	0,005	0,01	0,025	0,05	0,1
15	3,286041	2,946726	2,489878	2,131451	1,753051
16	3,251989	2,920788	2,47288	2,119905	1,745884
17	3,222449	2,898232	2,458055	2,109819	1,739606
18	3,196583	2,878442	2,445004	2,100924	1,734063
19	3,1737	2,860943	2,433444	2,093025	1,729131
20	3,1534	2,845336	2,423112	2,085962	1,724718

а) =0,05

б) =0,01

в) =0,1

г) =0,005

3.4.2. Оценка коэффициента  в уравнении парной линейной регрессии Y=+X+ тем точнее, чем

а) больше дисперсия объясняющей переменной Х;

б) больше объем выборки n;

в) меньше дисперсия отклонений ;

г) все три условия.

3.4.3. Оценка коэффициента  в уравнении парной линейной регрессии Y=+X+

а) пропорциональна коэффициенту корреляции r_XY;

б) пропорциональна коэффициенту детерминации R²;

в) обратно пропорциональна коэффициенту ;

г) все три условия.

3.4.4. Оценка коэффициента  в уравнении парной линейной регрессии Y=+X+

а) пропорциональна коэффициенту корреляции r_XY;

б) тем точнее, чем больше х_i²;

в) тем точнее, чем больше ;

г) все три утверждения верны.

3.4.5. Нулевая гипотеза для коэффициента регрессии b в уравнении парной линейной регрессии Y=a+bX+e проверяется с помощью

а) статистики Стьюдента;

б) стандартного нормального распределения;

в) статистики Фишера;

г) распределения Пуассона.

3.4.6. Стандартная ошибка коэффициента b в уравнении парной линейной регрессии Y=a+bX+e равна b/2, число наблюдений превышает 60. В этом случае можно утверждать, что

а) Y не зависит от X;

б) с вероятностью 70% Y зависит от X;

в) с вероятностью 70% Y не зависит от X;

г) с вероятностью 95% Y зависит от X;

4.1.1. По выборке из 20 наблюдений была оценена регрессия y=f(x₁,x₂,x₃). Для коэффициентов регрессии а₁,а₂,а₃ получены t-статистики: t₁= -2,2; t₂= 2,1; t₃= 2,5. По таблице функции распределения Стьюдента для двусторонней критической области определите, какие из оценок коэффициентов регрессии значимы с доверительной вероятностью 95%.

 / 	0,005	0,01	0,025	0,05	0,1
15	3,286041	2,946726	2,489878	2,131451	1,753051
16	3,251989	2,920788	2,47288	2,119905	1,745884
17	3,222449	2,898232	2,458055	2,109819	1,739606
18	3,196583	2,878442	2,445004	2,100924	1,734063
19	3,1737	2,860943	2,433444	2,093025	1,729131
20	3,1534	2,845336	2,423112	2,085962	1,724718

а) а₃

б) а₁,а₂,а₃

в) а₂,а₃

г) а₁,а₃

4.1.2. По выборке из 20 наблюдений была оценена регрессия y=f(x₁,x₂,x₃). Для коэффициентов регрессии а₁,а₂,а₃ получены t-статистики: t₁= -2,44; t₂= 2,1; t₃= 3,1. По таблице функции распределения Стьюдента для двусторонней критической области определите, с какой максимальной доверительной вероятностью значимы эти коэффициенты.

 / 	0,005	0,01	0,025	0,05	0,1
15	3,286041	2,946726	2,489878	2,131451	1,753051
16	3,251989	2,920788	2,47288	2,119905	1,745884
17	3,222449	2,898232	2,458055	2,109819	1,739606
18	3,196583	2,878442	2,445004	2,100924	1,734063
19	3,1737	2,860943	2,433444	2,093025	1,729131
20	3,1534	2,845336	2,423112	2,085962	1,724718

а) 99%

б) 90%

в) 95%

г) 97,5%

4.1.3. По выборке из 20 наблюдений была оценена регрессия y=f(x₁,x₂). Для коэффициентов регрессии а₁=100, а₂=150 получены значения стандартных отклонений : ₁= 33; ₂= 51. По таблице функции распределения Стьюдента для двусторонней критической области определите, с какой максимальной доверительной вероятностью коэффициенты регрессии значимы.

 / 	0,005	0,01	0,025	0,05	0,1
15	3,286041	2,946726	2,489878	2,131451	1,753051
16	3,251989	2,920788	2,47288	2,119905	1,745884
17	3,222449	2,898232	2,458055	2,109819	1,739606
18	3,196583	2,878442	2,445004	2,100924	1,734063
19	3,1737	2,860943	2,433444	2,093025	1,729131
20	3,1534	2,845336	2,423112	2,085962	1,724718

а) 99%

б) 99,5%

в) 97,5%

г) 95%

4.1.4. При исследовании зависимости себестоимости продукции y от объема выпуска x₁ и производительности труда x₂ по данным n=20 предприятий получено уравнение регрессии ŷ =2,88 – 0,72 x₁– 1,51 x₂и среднеквадратические отклонения коэффициентов регрессии: s_b1 =0,052 и s_b2=0,5. По таблице функции распределения Стьюдента для двусторонней критической области определите можно ли при уровне значимости =0,05 утверждать, что значимы коэффициенты регрессии

 / 	0,005	0,01	0,025	0,05	0,1
16	3,251989	2,920788	2,47288	2,119905	1,745884
17	3,222449	2,898232	2,458055	2,109819	1,739606
18	3,196583	2,878442	2,445004	2,100924	1,734063
19	3,1737	2,860943	2,433444	2,093025	1,729131
20	3,1534	2,845336	2,423112	2,085962	1,724718

а) b₁

б) b₂

в) оба значимы

г) оба незначимы

4.1.5. При исследовании зависимости себестоимости продукции y от объема выпуска x₁ и производительности труда x₂ по данным n=20 предприятий получено уравнение регрессии ŷ =2,88 – 0,72 x₁– 1,51 x₂. Приблизительно определите, на сколько процентов в среднем изменится себестоимость продукции y, если производительность труда x₂ увеличить на 1%, учитывая при этом :

а) 0,101%

б) –0,101%

в) –0,404%

г) 0,404%

4.1.6. По данным n =25 регионов получена регрессионная модель объема реализации медикаментов на одного жителя y в зависимости от доли городского населения x₁ и числа фармацевтов на 10 тыс. жителей x₂: ŷ =11,7 – 0,06x₁– 0,42x₂и среденеквадратические отклонения s_b1=0,04 и s_b2=0,14. По таблице функции распределения Стьюдента для двусторонней критической области определите, начиная с какого уровня значимости  можно утверждать, что y зависит от доли городского населения x₁:

 / 	0,1	0,2	0,3	0,4
22	1,717144	1,321237	1,061449	0,858266
23	1,71387	1,319461	1,060337	0,85753
24	1,710882	1,317835	1,059319	0,856855
25	1,70814	1,316346	1,058385	0,856236

а) 0,3

б) 0,2

в) 0,1

г) 0,05

4.2.1. Какой показатель характеризует долю объясненной с помощью регрессии дисперсии в общей дисперсии зависимой переменной?

а) коэффициент корреляции;

б) t–статистика;

в) F–статистика;

г) коэффициент детерминации.

4.2.2 Какой показатель характеризует долю объясненной с помощью регрессии дисперсии в общей дисперсии зависимой переменной?

а) ;

б) ;

в) , где ;

г) .

4.2.3. Для определения статистической значимости коэффициента детерминации R² проверяется нулевая гипотеза для F–статистики, рассчитываемая по формуле:

а) ;

б) ;

в) ;

г) .

5.3.1. Совершенную мультиколлинеарность нельзя определить следующим предложением:

а) столбцы матрицы Х, состоящей из m столбцов объясняющих переменных и единичного столбца, линейно зависимы;

б) матрица (Х^ТХ)^-1 имеет полный ранг m +1;

в) корреляция между некоторыми переменными х_i и х_j по модулю равна единице;

г) одна из объясняющих переменных линейно зависит от других.

5.3.2. В результате регрессионного анализа получена модель

y = 7,1 +0,6 х₁+0,4 х₂+0,1 х₃, t-статистики коэффициентов регрессии равны соответственно 24,5; 9,7; 0,7; 1,3. Коэффициент детерминации R²=0,9. Чем можно объяснить низкое качество коэффициентов регрессии при второй и третьей переменной?

а) тем, что количество наблюдений мало;

б) тем, что х₂ и х₃ фиктивные переменные;

в) тем, что х₂ и х₃ не влияют на y;

г) тем, что х₂ и х₃ линейно зависимы.

5.3.3. Признаком мультиколлинерности не является то, что

а) небольшое изменение исходных данных (например, добавление новых наблюдений) приводит к существенному изменению оценок коэффициентов модели;

б) невысокое значение коэффициента детерминации;

в) оценки коэффициентов регрессии имеют малую значимость при высоком значении коэффициента детерминации R² и соответствующей F-статистики;

г) оценки коэффициентов регрессии имеют неправильные с точки зрения теории знаки или неоправданно большие значения.

5.3.4. Матрица Х^ТХ (Х – регрессоры) близка к вырожденной (detX^TX~0). Это свидетельствует о

а) наличии фиктивной переменной;

б) наличии мультиколлинерности;

в) недостатке наблюдений в выборке;

г) о существовании переменных, влияющих на объясняемую переменную больше, чем переменные, входящие в набор Х.

5.3.5.Коэффициенты парной корреляции между тремя регрессорами следующие: r_x1x2=0,9; r_x1x3=0,5; r_x2x3=0,6. Это свидетельствует о мультиколлинеарности между объясняющими переменными. Какую из переменных следует исключить?

а) х₁;

б) х₂;

в) х₃;

г) для ответа на вопрос данных недостаточно

5.3.6. Корреляционная матрица для объясняемой переменной y (объем потребления) и объясняющих переменных х₁ (размер заработной платы); х₂ (трансферты); х₃ (доходы в целом) выглядит следующим образом:

у х₁ х₂ х₃

у 1

х₁ 0,4 1

х₂ 0,3 0,9 1

х₃ 0,5 0,75 0,82 1

Какое из уравнений регрессии можно идентифицировать?

а) у=а₁х₁+ а₂х₂+ а₃х₃+ а₀

б) у=а₁х₁+ а₃х₃+ а₀

в) у=а₂х₂+ а₃х₃+ а₀

г) у= а₃х₃+ а₀

5.3.7. Стоимость торта коррелирует с затратами в % муки, сливочного масла и сахара. При построении регрессионной модели следует ожидать эффекта мультиколлинерности между тремя основными ингредиентами. Как можно выявить фактор, наименее значимый в модели?

а) с помощью коэффициентов парной корреляции;

б) с помощью коэффициентов частной корреляции;

в) с помощью коэффициентов множественной корреляции;

г) с помощью коэффициента детерминации.

5.3.8. Мультиколлинеарность между объясняющими переменными возникает вследствие того, что

а) независимые переменные могут иметь общий временной тренд;

б) среди независимых переменных используются переменные, агрегирующие другие;

в) объясняющие переменные являются долями некоторого целого;

г) верны все три утверждения.

5.4.1. Переменные, принимающие только два значения 0 и 1 не называются

а) фиктивными;

б) двойственными;

в) бинарными;

г) dummy.

5.4.2. Фиктивные переменные позволяют исследовать

а) влияние качественных признаков;

б) влияние нескольких переменных, взаимосвязанных между собой;

в) сезонные различия;

г) верны все утверждения.

5.4.3. Для описания влияния образования (высшее, среднее, среднее специальное, неполное среднее) на уровень заработной платы следует ввести фиктивные переменные в количестве:

а) 1;

б) 2;

в) 3;

г) 4.

5.4.4. Объем продажи зонтиков от дождя зависит от сезона (зима, весна, лето, осень). Для учета сезонной составляющей следует ввести фиктивные переменные в количестве

а) 4;

б) 3;

в) 2;

г) 1.

5.4.5. Модель y = a₀ +a₁ х₁+a₂ х₂+a₃ х₃, где х₁ и х₂ принимают значения 0 и 1, а х₃ - положительное подходит для описания следующей ситуации

а) зависимость объема продаж тортов от цены в праздничные дни и в будни;

б) зависимость объема продаж тортов от цены в выходные, праздничные дни и в будни;

в) зависимость объема продаж от цены зонтиков от дождя в различные времена года;

г) зависимость объема продаж велосипедов от цены в периоды с октября по март и с апреля по сентябрь включительно.

5.4.6. Модель y = a₀ +a₁ х₁+a₂ х₂ описывает зависимость объема потребления y городских и сельских жителей от уровня дохода х₂ в предположении одинаковой предельной склонности к потреблению у этих групп. Сдвиг в объеме потребления между этими группами жителей по абсолютной величине равен

а) a₀

б) a₁

в) х₁

г) a₂

5.6.1. Выберите уравнения, которые могут быть преобразованы в уравнения, линейные по параметрам:

1. Y_i=exp(x_i)_i

2. Y_i=exp(-x_i)+_i

3. Y_i=exp(+x_i+_i)

4. Y_i=/exp(-x_i)+_i

а) 1 и 3 б) 2 и 4 в) 1 и 4 г) 2 и 3

5.6.2. При каких условиях на параметры  и  производственная функция в модели Кобба-Дугласа Y=AK^L^ может быть преобразована в парную линейную регрессию по этим параметрам?

а) при <1 и <1

б) при =1

в) при +=1

г) при любых

6.1.1. В чем состоит условие гомоскедастичности в регрессионной модели, если t₁,t₂=1,2,…,n и t₁t₂:

а) M[_t1_t2]=0;

б) M[_t1] M[_t2]

в) M[²_t1]= M[²_t2]

г) M[_t1_t2] 0

6.1.2. В чем состоит условие гетероскедастичности в регрессионной модели, если t₁,t₂=1,2,…,n и t₁t₂:

а) M[_t1] =M[_t2]

б) M[²_t1]= M[²_t2]

в) M[_t1_t2] 0;

г) M[²_t1] M[²_t2]

6.1.3. Какие оценки коэффициентов регрессии будут иметь наименьшую дисперсию, если матрица ковариаций ошибок cov(e_i,e_j) имеет следующий вид:

а) оценки, полученные с помощью метода наименьших квадратов;

б) оценки, полученные с помощью обобщенного метода наименьших квадратов;

в) оценки, полученные с помощью взвешенного метода наименьших квадратов;

г) другое.

6.1.4. Оценка параметров a уравнения регрессии y=Xa получена обобщенным методом наименьших квадратов. Это означает, что она получена в результате решения оптимизационной задачи, в которой критерием оптимальности выступает:

а) F(a) = (y-Xa)^T(y-Xa) min;

б) F(a) = (y-Xa)^TV(y-Xa) min, где V – матрица ковариаций ошибок;

в) F(a) = (y-Xa)^TV^-1(y-Xa) min, где V – матрица ковариаций ошибок;

г) F(a) = (y-Xa)^T(X^TX)^-1(y-Xa) min.

6.3.1. Матрица ковариаций ошибок имеет вид

, где s_i  s_j при i  j

Это свидетельствует о наличии

а) авторегрессии ошибок;

б) автокорреляции ошибок:

в) гетероскедастичности;

г) гомоскедастичности.

6.3.2. Если ошибки регрессии порождаются авторегрессионным процессом 1-го порядка: e_i=e_i-1+u_i, где e_i – i-тая ошибка регрессии, - коэффициент авторегрессии, u_i - «белый шум», то ковариационная матрица может быть представлена в виде:

а)

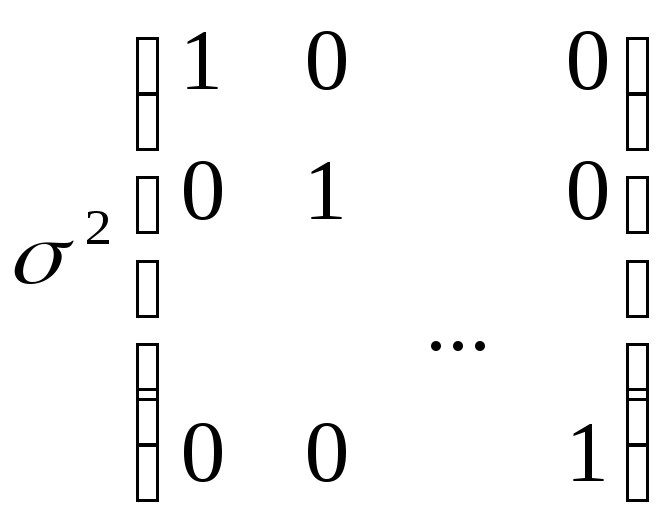
б)

в)

г)

6.3.3 Наличие автокорреляции в модели может быть выражено следующей записью (t=2,…,n ):

а) M[_t] M[_t-1];

б) D[_t] D[_t-1];

в) M[_t_t-1] =0;

г) r_t,t-1 0.

7.1 Цена на двухкомнатные квартиры price зависит от общей площади totsq, площади кухни kitsq и расстояния от центра dist следующим образом:

price= 235,6+ 1,8 totsq +1,6 kitsq – 1,7 dist

При этом дисперсия ошибок составляет s²=35,24. В каких пределах может находится цена на квартиру с параметрами totsq=32; kitsq=6; dist=15 с вероятностью 95% (t=1,96).

а) [208,23; 346,37];

б) [265,67; 288,94];

в) [275,34; 279,26];

г) [242,06; 312,54].

7.2 Цена на двухкомнатные квартиры price зависит от общей площади totsq, площади кухни kitsq и расстояния от центра dist следующим образом:

price= 235,6+ 1,8 totsq +1,6 kitsq – 1,7 dist

При этом дисперсия ошибок составляет s²=35,24. В каких пределах может находится цена на квартиру с параметрами totsq=40; kitsq=8; dist=5 с вероятностью 95% (t=1,96).

а) [300,27; 323,54];

б) [309,94; 313,86];

в) [276,66; 347,14];

г) [242,83; 380,97].

7.3. Цена на однокомнатные квартиры price зависит от общей площади totsq, площади кухни kitsq и расстояния от автобусной остановки dist следующим образом:

price= 184,8+ 2,8 totsq +1,3 kitsq – 3,7 dist

При этом дисперсия ошибок составляет s²=51,7. В каких пределах может находится цена на квартиру с параметрами totsq=40; kitsq=8; dist=5 с вероятностью 95% (t=1,96).

а) [237; 340,4];

б) [274,61; 302,79];

в) [187,37; 390,03];

г) [286,74; 290,66].

7.4. Цена на однокомнатные квартиры price зависит от общей площади totsq, площади кухни kitsq и расстояния от автобусной остановки dist следующим образом:

price= 184,8+ 2,8 totsq +1,3 kitsq – 3,7 dist

При этом дисперсия ошибок составляет s²=51,7. В каких пределах может находится цена на квартиру с параметрами totsq=40; kitsq=8; dist=5 с вероятностью 99% (t=2,58).

а) [155,53; 421,87];

б) [286,12; 291,28];

в) [270,18; 307,22];

г) [237; 340,4].

7.5. Цена на однокомнатные квартиры price зависит от общей площади totsq, площади кухни kitsq и расстояния от автобусной остановки dist следующим образом:

price= 184,8+ 2,8 totsq +1,3 kitsq – 3,7 dist

При этом дисперсия ошибок составляет s²=31,7. В каких пределах может находится цена на квартиру с параметрами totsq=30; kitsq=4; dist=4 с вероятностью 99% (t=2,58).

а) [244,7; 273,7];

б) [177,55; 340,85];

в) [256,62; 261,78];

г) [227,5; 290,9].

7.6. Интервальная оценка при прогнозировании значения случайной величины зависит от

а) заданного уровня вероятности;

б) дисперсии случайной величины;

в) среднего значения случайной величины;

г) всего вышеперечисленного.

7.7. Интервальный прогноз в регрессионной модели будет тем менее достоверным, чем далее удалена точка X_n+1 относительно если

а) известны коэффициенты регрессии и ошибки гомоскедастичны;

б) известны оценки коэффициентов регрессии и ошибки гомоскедастичны;

в) известны оценки коэффициентов регрессии и ошибки автокоррелированы;

8.1.1. Временной ряд x(t) называется строго стационарным (в узком смысле слова) если

а) закон распределения вероятностей случайной величины x(t) не зависит от t;

б) среднее значение случайной величины x(t) постоянно для любого t;

в) дисперсия случайной величины x(t) постоянна для любого t;

г) среднее значение случайной величины x(t) постоянно для любого t и равно 0.

8.2.1. Автоковариационная функция в предположении строгой стационарности ряда x_t для (0) равна:

а) r[x_t1x_t2]

б) cov[x_t1x_t2]

в) D[x_t]

г) M[x_t]

8.3.1. Какой метод не используется для сглаживания стационарного временного ряда?

а) метод скользящего среднего

б) метод серий, основанных на медиане

в) метод подбора аппроксимирующего полинома

г) метод Брауна

8.4.1. Для модели авторегрессионного преобразования АР(1) (t)=(t-1)+u(t) известны значения автоковариационной функции (1)=1,3 и (0)=1,5. Чему равен коэффициент ?

а) 2,8;

б) 0,87;

в) 1,15;

г) –0,2;

8.4.2. Для модели авторегрессионного преобразования АР(1) (t)=(t-1)+u(t) известны значения автоковариационной функции (1)=1,2 и (0)=1,7. Чему равен коэффициент ?

а) 2,04;

б) 1,41;

в) 0,71;

г) 2,9.

8.4.3. Для модели авторегрессионного преобразования АР(1) (t)=(t-1)+u(t) известны значения автоковариационной функции (1)=1,1 и (0)=2,7. Чему равен коэффициент ?

а) 0,41;

б) 2,45;

в) 3,8;

г) 2,87.

8.4.4. Для модели авторегрессии второго порядка АР(1) (t) = ₁(t-1) + ₂(t-2) + u(t) верно следующее утверждение:

а) (1) = ₁(0) + ₂(2)

б) (0) = ₁(1) + ₂(2)

в) (1) = ₁(0) + ₂(1)

г) (1) = ₁(2) + ₂(0)

8.4.5. Известен вид модели авторегрессионного преобразования АР(2) . Какое из следующих утверждений верно для автоковариационной функции ()?

а) (1) = 2,5(0) + 4,5(2)

б) (0) = 2,5(1) + 4,5(2)

в) 3,5(1) = -2,5(0)

г) (1) = 2,5(2) + 4,5(0)

8.4.6. Известен вид модели авторегрессионного преобразования АР(2) . Какое из следующих утверждений верно для автоковариационной функции ()?

а) (1) = 4,5(0) + 2,5(2)

б) (0) = 4,5(1) + 2,5(2)

в) (1) = 4,5(2) + 2,5(0)

г) (1) = -3(0)

8.4.7. Известен вид модели авторегрессионного преобразования АР(2) . Какое из следующих утверждений верно для автоковариационной функции ()?

а) (1) = 5(0) + 2(2)

б) (1) + 5(0) = 0

в) (1) = 5(2) + 2(0)

г) (0) = 5(1) + 2(2)

8.4.8. Известен вид модели авторегрессионного преобразования АР(3) . Какое из следующих утверждений верно для автоковариационной функции ()?

а) 4,5(0) = -2,5(2)

б) (2) = 5,5(1) + 2,5(0)

в) (1) = 4,5(2) + 2,5(0) + (1)

г) (1) = -3,5(0) + (2)

8.4.9. Известен вид модели авторегрессионного преобразования АР(3) . Какое из следующих утверждений верно для автокорреляционной функции ()?

а) 4,5(1) = -2,5(2)

б) (2) = 4,5(1)

в) (2)= -4,5 - 2,5(1)

г) (2) = 5,5(1) + 2,5

9.2.1. Какая из систем регрессионных уравнений относится к рекурсивной модели:

а) y_1,t=₁(x_1,t;y_2,t-1;x_2,t-1)

y_2,t=₂(y_1,t;x_1,t; x_2,t)

б) y_1,t=₁(x_1,t;y_2,t;x_2,t-1)

y_2,t=₂(y_1,t; y_2,t-1;x_1,t)

в) y_1,t=₁(y_2,t;x_1,t; x_2,t-1)

y_2,t=₂(y_1,t;x_t; x_2,t)

г) y_1,t=₁(x_1,t;y_2,t;x_1,t-1)

y_2,t=₂(y_1,t;x_1,t-1; x_2,t-2)

9.3.1. При нахождении оценок параметров системы одновременных эконометрических уравнений не используется:

а) трехшаговый метод;

б) косвенный метод:

в) метод скользящих средних;

г) двухшаговый метод.

10.1.1. Плотность вероятности распределения на заданном интервале одинакова. Такое распределение называется

а) равновероятным

б) нормальным

в) биномиальным

г) равномерным

10.1.2. Какова вероятность попадания реализации случайной величины R(1;5) в интервал (-;2]?

а) 0,5

б) 1

в) 0,25

г) 0,75

10.2.1. Если ряд случайных величин (X₁,X₂, …X_n) имеет нормальное распределение, то их линейная комбинация (₁X₁+₂X₂+ …+_nX_n) будет иметь

а) нормальное распределение

б) распределение Стьюдента

в) распределение Фишера

г) равномерное распределение

10.2.2. Какова вероятность попадания реализации случайной величины N(1;100) в интервал (-;1]?

а) 0,5

б) 1

в) 0,25

г) 0,75

10.2.3. По таблице функции распределения стандартного нормального распределения определите, какова вероятность попадания реализации случайной величины N(1;10) в интервал (-;2]?

Z	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0	0,5	0,503989	0,507978	0,511967	0,515953	0,519939	0,523922	0,527903	0,531881	0,535856
0,1	0,539828	0,543795	0,547758	0,551717	0,55567	0,559618	0,563559	0,567495	0,571424	0,575345
0,2	0,57926	0,583166	0,587064	0,590954	0,594835	0,598706	0,602568	0,60642	0,610261	0,614092
0,3	0,617911	0,621719	0,625516	0,6293	0,633072	0,636831	0,640576	0,644309	0,648027	0,651732
0,4	0,655422	0,659097	0,662757	0,666402	0,670031	0,673645	0,677242	0,680822	0,684386	0,687933

а) 0,5

б) 0,503989

в) 0,539828

г) 0,57926