10.4.2. Примеры расчетов вероятности попадания в заданный интервал с помощью таблиц t-распределения Стьюдента

В таблице функции распределения Стьюдента приводятся обычно, для различных чисел степеней свободы , критические точки, соответствующие приведенным в верхней строке таблицы вероятностямпопадания в правый «хвост» распределения. Иными словами, в приведенной ниже таблице число- это вероятность превышенияt–статистикой приведенного в таблице критического значения при соответствующем числе степеней свободы (более подробная таблица приведена в прил.1):

Таблица 10.2

\	0,005	0,01	0,025	0,05	0,1
1	63,657	31,821	12,706	6,314	3,078
…	…	…	…	…	…
10	3,169	2,764	2,228	1,812	1,372
…	…	…	…	…	…
30	2,750	2,457	2,042	1,697	1,310
	2,576	2,326	1,960	1,645	1,282

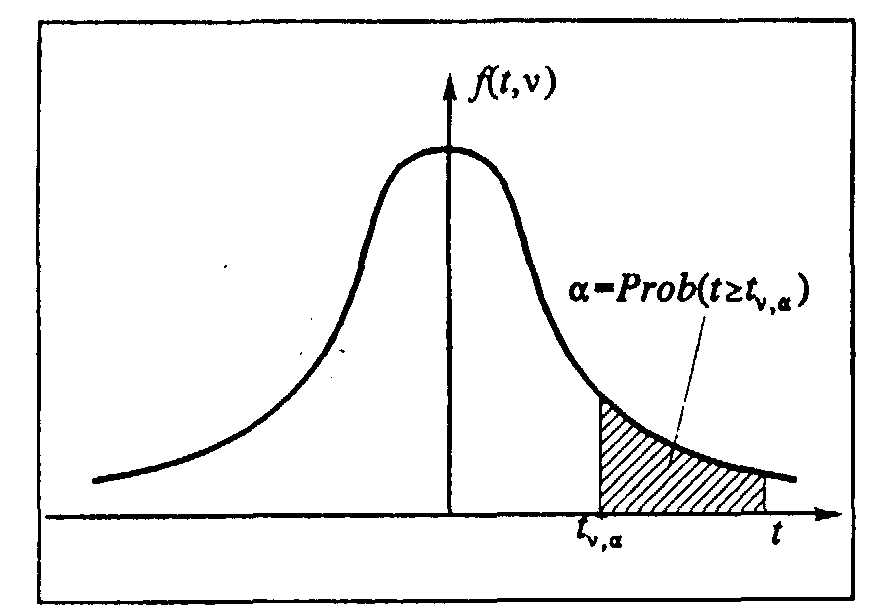
Рис. 10.7. Односторонняя критическая область распределения Стьюдента

Критическая точка t_,(например,t_10;0,05) находится на пересечении строки с числом степеней свободы (в данном случае=10) и столбца с заданной вероятностью (в данном случае=0,05). Из приведенной таблицы находим, чтоt_10,0,05=1,812. Напомним, что критическая точка в данном случае имеет смысл:Prob{t>t_,}=.

Отметим, что иногда таблицы распределения Стьюдента приводятся для двусторонних критических точек t^s_,, определяемых их условияProb{t>t^s_,}=.

Рис. 10.8. Двусторонняя критическая область распределения Стьюдента

В силу симметричности распределения Стьюдента эти точки связаны с односторонними критическими точками соотношением t^s_,= t_,/2,так как при заданной вероятности а попадания в оба "хвоста" распределения вероятность попадания в один из "хвостов" распределения будет в два раза меньше и равна/2.

Кроме того, в некоторых таблицах распределения Стьюдента вместо малых чисел (вероятностей попадания в "хвост" распределения) приводятся числа 1-(вероятности попадания в интервал (-, t_,) для односторонних критических точек и в интервал [-t^s_,,t^s_,) для двусторонних критических точек).

10.5. F-распределение Фишера

Это распределение (называемое иногда распределением дисперсионного отношения) имеет случайная величина, равная отношению двух независимых случайных величин: величины выражающейся через случайную величину, имеющую распределение² сk₁ степенями свободы и величинывыражающейся через случайную величину, имеющую распределение² сk₂ степенями свободы (распределение², имеет сумма квадратовk₁ независимых стандартно нормально распределенных случайных величин).

Вводя новую случайную величину , мы получим для нее распределение Фишера сk₁иk₂степенями свободы с плотностью вероятности:

, (10. 0)

. (10. 0)

Рис. 10.9. F-распределение Фишера

1^о. Критические точки распределения Фишера обладают следующим свойством:

(10. 0)

2^о. Квадрат случайной величины, имеющей распределение Стьюдента сk₂степенями свободы, имеет распределение Фишера с (1,k₂) степе­нями свободы.

Подставляя в определение случайной величины F«выборочное представление случайной величины, можно получить «выборочное представление» случайной величиныF:

(10. 0)

где - исправленная выборочная дисперсия для выборки объемап.

Распределение Фишера используется, например, при:

• сравнении двух дисперсий;

• проверке гипотезы об одновременном равенстве нулю всех или части коэффициентов линейной регрессии;

• проверке гипотезы о совпадении всех коэффициентов двух уравнений линейной регрессии.