
- •Введение
- •Основные понятия теории вероятностей
- •1.1. События и действия над ними
- •1.2. Определение вероятности
- •1.3. Элементы комбинаторики
- •1.4. Условная вероятность события
- •1.5. Вероятность суммы двух событий
- •1.6. Формула полной вероятности. Формула Байеса
- •Упражнения
- •2. Повторные независимые испытания
- •2.1. Формула Бернулли
- •2.2. Формула Пуассона
- •2.3. Локальная и интегральная формулы Муавра-Лапласа
- •2.4. Полиномиальная схема
- •Упражнения
- •3. Случайные величины
- •3.1. Закон распределения случайной величины
- •Математические операции над случайными величинами
- •3.3. Математическое ожидание и дисперсия дискретной случайной величины
- •3.4. Функция распределения случайной величины
- •3.5. Непрерывные случайные величины
- •Упражнения
- •4. Основные законы распределения
- •4.1. Биномиальное распределение
- •4.2. Закон распределения Пуассона
- •4.3. Равномерный закон распределения
- •4.4. Показательный закон распределения
- •4.5. Нормальный закон распределения
- •Упражнения
- •5. Закон больших чисел и предельные теоремы
- •5.1. Неравенство Маркова
- •5.2. Неравенство Чебышева
- •5.3. Теорема Чебышева
- •5.4. Центральная предельная теорема
- •Упражнения
- •6. Однородные цепи Маркова
- •Упражнения
- •7. Занимательная теория вероятностей
- •7.1. Занимательные задачи
- •7.2. Парадоксы теории вероятностей
- •Упражнения
- •9. Статистическое распределение выборки
- •Упражнения
- •Упражнения
- •11. Статистические оценки параметров распределения
- •11.1. Точечные оценки
- •Упражнения
- •11.2. Интервальные оценки
- •Упражнения
- •Упражнения
- •13. Статистическая проверка гипотез о вероятностях,
- •средних, дисперсиях. Критерий согласия Пирсона
- •Упражнения
- •14. Регрессия и корреляция
- •14.1. Функциональная, статистическая и корреляционная зависимости
- •14.2. Линейная модель парной регрессии
- •14.3. Корреляционная таблица. Коэффициент корреляции
- •Упражнения
- •Домашняя контрольная работа
- •Библиографический список
- •Приложения. Математико-статистические таблицы
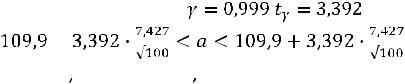
При надежности |
; подставляя данные, получаем: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или 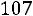
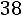
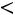
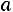
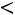
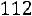
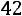 .
. 
Упражнения
13.1. В результате опыта получено 100 значений признака, составляющих выборку из генеральной совокупности. Данные приведены в таблицах 13.1, 13.2:
Задание:
1.Составить вариационный ряд.
2.Составить статистический ряд частот.
3.Составить сгруппированный статистический ряд.
4.Построить гистограмму частот.
5.Записать значения и построить график эмпирической функции.
6.Найти выборочное среднее, выборочную дисперсию, среднеквадратическое отклонение, асимметрию, эксцесс.
7.Выдвинуть гипотезу о нормальном распределении по виду графика эмпирической функции, гистограммы частот, по величинам асимметрии и эксцесса.
8.Построить кривую плотности нормального распределения.
9.Применить критерий Пирсона с уровнем значимости 0,05 для окончательного принятия или отклонения гипотезы о нормальном распределении генеральной совокупности.
10.Оценить математическое ожидание генеральной совокупности
спомощью доверительного интервала с надежностями 0,95, 0,99, 0,999. Значение наблюдаемого признака выбирается обучающимся из таб-
лицы 13.2 в зависимости от номера варианта. Номер варианта определяется из таблицы 13.1 по последней цифре номера зачетной книжки.
Таблица 13.1
Но- |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
мер |
|
|
|
|
|
|
|
|
|
|
вари- |
|
|
|
|
|
|
|
|
|
|
анта |
|
|
|
|
|
|
|
|
|
|
Но- |
1–10 |
2–11 |
3–12 |
4–13 |
5–14 |
6–15 |
7–16 |
8–17 |
9–18 |
10–19 |
мера |
|
|
|
|
|
|
|
|
|
|
строк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
99 |
|
|
|
|
|
