3. «Правило трех сигм». Практически достоверно, что значения нормально распределенной случайной величины заключены в интервале

в результате опыта примет значение, заключенное в интервале (12,5; 14).

■

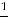
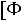
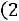
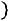
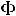
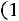
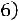
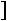
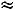
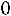
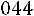
Упражнения

4.1.Вероятность выигрыша в лотерее равна 0,1. Cоставить закон распределения числа выигравших билетов среди 10 приобретенных. Найти математическое ожидание и дисперсию этой случайной величины.

4.2.Устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента равна 0,002. Необходимо: а) составить закон распределения отказавших элементов; б) найти математическое ожидание и дисперсию этой случайной величины; в) определить вероятность того, что откажет хотя бы один элемент. От-

вет: в) 0,865.

4.3.Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (15, 25).

4.4.Случайная величина Z подчиняется стандартному нормальному закону распределения. Найти вероятность попадания Z в интервалы: а) от

2 до 3; б) менее 2,1.

4.5.Текущая цена акции может быть смоделирована спомощью нормального закона распределения с математическим ожиданием 15 ден. ед.

исредним квадратическим отклонением 0,2 ден. ед. 1. Найти вероятность того, что цена акции: а) не выше 15,3 ден. ед.; б) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3 ден. ед. 2. С помощью правила трех сигм найти границы, в которых будет находиться текущая цена акции. Ответ: 1.

а) 0,9332; б) 0,0228; в) 0,6246; 2.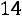

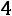
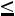
50