Т е м а 8. Преобразование лоренца

8.1. Пусть для измерения времени используется периодический процесс отражения светового “зайчика” попеременно от двух зеркал, укрепленных на концах стержня длиной l. Один период — это время движения зайчика от одного зеркала до другого и обратно. Световые часы неподвижны в системе и ориентированы параллельно направлению движения. Пользуясь постулатом о постоянстве скорости света, показать, что интервал собственного временивыражается через промежуток времени dt в системе S формулой

.

8.2. Какой промежуток времени занял бы по земным часам полет ракеты до звездной системы Проксима-Центавра и обратно (расстояние до нее 4 световых года), если бы он осуществлялся с постоянной скоростью? Из расчета какой длительности путешествия следовало бы запасаться продовольствием и другим снаряжением? Какой запас кинетической энергии в такой ракете, если ее масса 10 т?

8.3. Два пучка электронов летят навстречу друг другу со скоростью относительно лабораторной системы координат. Какова относительная скорость V электронов:

а) с точки зрения наблюдателя в лаборатории;

б) с точки зрения наблюдателя, движущегося с одним из пучков электронов?

8.4. Ракета, рассматриваемая в задаче 8.2., разгоняется от состояния покоя до скорости . Ускорение ракеты составляетм/с² в системе, мгновенно сопутствующей ракете. Сколько времени длится разгон ракеты по часам в неподвижной системе отсчета и по часам в ракете.

Указание: Влияние сил инерции на ход часов не учитывать. Это означает, что предполагается вычислить сумму собственных времен в последовательности мгновенно сопутствующих ракете инерциальных систем отсчета, выражаемую интегралом.

8.5. Пучок света в некоторой системе отсчета образует телесный угол . Как изменится этот угол при переходе к другой инерциальной системе отсчета?

8.6. Длина волны света, излучаемого некоторым источником, в той системе, в которой источник покоится, равна . Какую длину волнызарегистрируют:

а) наблюдатель, приближающийся со скоростью V к источнику, и б) наблюдатель, удаляющийся с такой же скоростью от источника?

8.7. Плоская волна распространяется в движущейся со скоростью V среде в направлении перемещения среды. Длина волны в вакууме . Найти скорость v волны относительно лабораторной системы (опыт Физо). Показатель преломления n определяется в системе, связанной со средой, и зависит от длины волныв этой системе. Вычисления проводить с точностью до первого порядка по v/c.

Т е м а 9-10. Релятивистские электродинамика и механика

9.1. В системе отсчета S электрическое и магнитное поля взаимно перпендикулярны: . С какой скоростью относительно S должна двигаться система, в которой имеется только электрическое или магнитное поле? Всегда ли существует решение и единственно ли оно?

9.2. Бесконечно длинный круговой цилиндр равномерно заряжен с линейной плотностью . Вдоль оси цилиндра течет равномерно распределенный ток I. Во всем пространстве проницаемость. Найти такую систему отсчета, в которой существует только электрическое или только магнитное поле. Найти величину этих полей.

9.3. Электрический диполь с моментом в системе покоя равномерно движется со скоростью. Найти создаваемое им электромагнитное полеи.

10.1. Выразить импульс релятивистской частицы через ее кинетическую энергию Т.

10.2. Выразить скорость 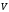частицы через ее импульс.

10.3. Частица с массой m обладает энергией Е. Найти скорость v частицы. Рассмотреть, в частности, нерелятивистский и ультрарелятивистский пределы.

10.4. Найти скорость V частицы с массой m и зарядом e, прошедшей разность потенциалов U (начальная скорость равна нулю). Упростить общую формулу для нерелятивистского и ультрарелятивистского случаев (учесть по два члена разложения).

10.5. Частица с массой m₁ и скоростью v сталкивается с покоящейся частицей массы m₂ и поглощается ею. Найти массу m и скорость V образовавшейся частицы.

10.6. Ускоритель дает на входе пучок заряженных частиц с кинетической энергией T; сила тока в пучке равна I. Найти силу F давления пучка на поглощающую его мишень и выделяемую в мишени мощность W. Масса частицы m, заряд e.