
- •Задачи по электродинамике
- •Т е м а 3. Электростатическое поле. Уравнение пуассона
- •Т е м а 4. Стационарное магнитное поле. Векторный потенциал. Закон био — савара — лапласа
- •Т е м а 5. Разложение эликтрического поля по мультиполям
- •Т е м а 6. Дифракция электромагнитных волн
- •Т е м а 7. Движение заряженных частиц. Излучение электромагнитных волн
- •Т е м а 8. Преобразование лоренца
- •Т е м а 9-10. Релятивистские электродинамика и механика
- •Т е м а 11. Релятивистское движение заряженных частиц в электромагнитном поле
- •Т е м а 12-13. Поляризация вещества. Диэлектрическая проницаемость
- •Т е м а 14-15. Плоские электромагнитные волны. Волновое уравнение. Поляризация. Отражение и преломление электромагнитных волн
- •Рекомендуемый библиографический список
Т е м а 6. Дифракция электромагнитных волн
6.1.* Найти волновое возмущение в области z>0, если все источники волн находятся в области z<0 и известно волновое возмущение в плоскости z=0.
6.2.* Рассмотреть интегральное соотношение Зоммерфельда для электромагнитного поля
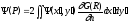
и выразить напряженность электрического поля в области z>0 через тангенсальные составляющие вектора напряженности электрического поля в плоскости дифракции.
6.3. Рассмотреть дифракцию электромагнитных волн на щели для двух случаев поляризации падающего излучения.
6.4. Черный экран с круглым отверстием радиуса а расположен в плоскости x, y так, что центр отверстия совпадает с началом координат. Найти точки на положительной оси (z>>a), где интенсивность приблизительно равна нулю, если на экран падает плоская волна
 .
.
6.5.
Точечный источник электромагнитной
волны расположен на оси, проходящей
через центр круглого непрозрачного
экрана радиуса а перпендикулярно его
плоскости. Считая выполненным условие
 ,
где
,
где —
длина волны, найти интенсивность
электромагнитного возмущения I в
симметричной относительно экрана точке
Р.
—
длина волны, найти интенсивность
электромагнитного возмущения I в
симметричной относительно экрана точке
Р.
6.6. Рассмотреть дифракцию на круглом отверстии в бесконечном непрозрачном экране. Условия дифракции аналогичны задаче 6.5.
6.7. Параллельный пучок электромагнитных волн падает на круглое отверстие в непрозрачном экране перпендикулярно ее плоскости. Найти распределение интенсивности на средней линии за экраном.
Т е м а 7. Движение заряженных частиц. Излучение электромагнитных волн
7.1.
Поверхность шара равномерно покрыта
слоем радиоактивного вещества, которое
испускает
 -частицы
высокой энергии. Вообразим, что
-частицы
высокой энергии. Вообразим, что -частицы
вылетают только наружу от поверхности
шара, причем только в радиальном
направлении. С поверхности шара тем
самым стекают заряды, то есть течет
некоторый ток. Создает ли этот ток
магнитное поле?
-частицы
вылетают только наружу от поверхности
шара, причем только в радиальном
направлении. С поверхности шара тем
самым стекают заряды, то есть течет
некоторый ток. Создает ли этот ток
магнитное поле?
7.2.
По малому участку внутри однородного
проводника в начальный момент распределен
заряд с объемной плотностью
 ,
представленный потом самому себе заряд
стекает на поверхность проводника. Как
будет при этом изменяться плотность
заряда на указанном участке? Каково
время релаксации процесса растекания
заряда в проводнике?
,
представленный потом самому себе заряд
стекает на поверхность проводника. Как
будет при этом изменяться плотность
заряда на указанном участке? Каково
время релаксации процесса растекания
заряда в проводнике?
7.3. Показать, что при релаксации зарядов в однородной проводящей среде ток смещения точно компенсирует ток проводимости, так что магнитное поле в процессе релаксации зарядов не создается.
7.4. Определить полную среднюю интенсивность дипольного излучения вибратора Герца, дипольный момент которого изменяется со временем по закону:
 .
.
7.5. Оценить, за какое время электрон, обращающийся по круговой орбите в атоме водорода, упадет на ядро вследствие излучения электромагнитных волн.
7.6. Определить интенсивность электромагнитного излучения системы заряженных частиц (с зарядами e1 и e2 и массами m1 и m2), взаимодействующих по закону Кулона.
7.7.
Классический осциллятор в отсутствие
поля колеблется с частотой
 .
Найти изменение частоты колебаний
осциллятора при включении постоянного
однородного магнитного поля
.
Найти изменение частоты колебаний
осциллятора при включении постоянного
однородного магнитного поля .
Указать результат решения задачи для
случая слабого магнитного поля.
.
Указать результат решения задачи для
случая слабого магнитного поля.
7.8.
Электрон влетает в однородное магнитное
поле
 со скоростью
со скоростью ,
направление которой образует угол
,
направление которой образует угол с направлением линий поля. Показать,
что время, в течение которого электрон
описывает один виток винтовой траектории,
не зависит ни от скорости
с направлением линий поля. Показать,
что время, в течение которого электрон
описывает один виток винтовой траектории,
не зависит ни от скорости ,
ни от угла
,
ни от угла .
.
7.9.
Показать, что в волновой зоне при
выполнении условия Лоренца скалярный
потенциал ограниченной излучающей
системы может быть выражен через
векторный потенциал формулой
 ,
где
,
где —
радиус-вектор точки наблюдения.
—
радиус-вектор точки наблюдения.
