
- •Задачи по электродинамике
- •Т е м а 3. Электростатическое поле. Уравнение пуассона
- •Т е м а 4. Стационарное магнитное поле. Векторный потенциал. Закон био — савара — лапласа
- •Т е м а 5. Разложение эликтрического поля по мультиполям
- •Т е м а 6. Дифракция электромагнитных волн
- •Т е м а 7. Движение заряженных частиц. Излучение электромагнитных волн
- •Т е м а 8. Преобразование лоренца
- •Т е м а 9-10. Релятивистские электродинамика и механика
- •Т е м а 11. Релятивистское движение заряженных частиц в электромагнитном поле
- •Т е м а 12-13. Поляризация вещества. Диэлектрическая проницаемость
- •Т е м а 14-15. Плоские электромагнитные волны. Волновое уравнение. Поляризация. Отражение и преломление электромагнитных волн
- •Рекомендуемый библиографический список
Министерство общего и профессионального образования
Российской Федерации
СЫКТЫВКАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра физики твердого тела
Задачи по электродинамике
Методические указания
к практическим занятиям
Сыктывкар 1999
Методические указания по курсу электродинамики рассчитаны на студентов-физиков с учетом существующих программ по электродинамике. Предложенные задачи требуют соответствующей математической подготовки. Большинство из них решаются простыми математическими методами. Несколько задач выделяется по своей сложности и их решение связано с трудоемкими вычислениями. Эти задачи отмечены звездочкой.
В методических указаниях используется гауссова система единиц, так как она наиболее часто употребляется в физической литературе.
Т е м а 1, 2. ВЕКТОРНЫЙ АНАЛИЗ В КУРСЕ ЭЛЕКТРОДИНАМИКИ
Разложение вектора
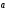 по ортам
по ортам ,
, ,
,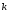 декартовой системы координат имеет
вид:
декартовой системы координат имеет
вид:
 .
.
Некоторые сведения из векторного анализа:
1.
Скалярное произведение двух векторов
 и
и :
:
 ,
,
 ,
,
 —
угол между
—
угол между и
и ;
;
2.
Векторное произведение двух векторов
 и
и :
:
 ,
,
 ,
,
где
 — угол между
— угол между и
и ;
;
3. Смешанное произведение:
 ;
;
4. Двойное векторное произведение:
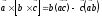 .
.
5.
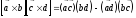 .
.
Дифференциальные операции:
1. Дифференцирование вектора, зависящего от скалярного аргумента
 ,
,
где
 — единичный вектор по направлению
— единичный вектор по направлению .
.
2.
Полная производная от
 по времени t
по времени t
 ,
,
где
 — векторный дифференциальный оператор.
— векторный дифференциальный оператор.
3.
Пусть
 ,
где u — скалярный аргумент, зависящий
от координат:
,
где u — скалярный аргумент, зависящий
от координат:
 ,
,
 .
.
Задания.
1.1.
С помощью оператора
 ,
пользуясь правилами дифференцирования
и перемножения векторов, доказать
тождества:
,
пользуясь правилами дифференцирования
и перемножения векторов, доказать
тождества:
1.

2.

3.

4.

5.

6.

7.
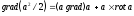
8.

9.
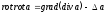
10.

1.2. Вычислить:
 ,
,
 ,
,
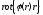 ,
,
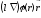 .
.
1.3. Доказать тождества:
1.

2.

3.

4.

5.

6.

1.4. В некоторых случаях бывает удобно вместо декартовых компонент вектора аx, ay, az рассматривать его циклические компоненты, определяемые формулами:
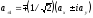 ,
,
 .
.
Выразить скалярные и векторные произведения двух векторов через их циклические компоненты.
1.5. Записать циклические компоненты градиента в сферических координатах (см. задачу 1.4.).
1.6.
Найти функцию
 ,
удовлетворяющую условию:
,
удовлетворяющую условию:
 .
.
1.7. Найти дивергенции и вихри следующих векторов:
1.

2.

3.

4.

5.
 ,
,
где
 и
и — постоянные векторы.
— постоянные векторы.
1.8. Вычислить
 ,
,
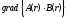 ,
,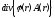 ,
,
 ,
,
 ,
,
где
 .
.
Т е м а 3. Электростатическое поле. Уравнение пуассона
3.1.
Объемная плотность заряда полупространства
 имеет периодическую структуру
имеет периодическую структуру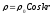 ,
где постоянный вектор
,
где постоянный вектор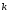 образует с осью z отличный от нуля угол.
Найти потенциал
образует с осью z отличный от нуля угол.
Найти потенциал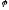 электрического поля в каждой точке
пространства.
электрического поля в каждой точке
пространства.
Решение: Потенциал
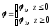 (1)
(1)
является решением уравнений
 ,
,
 (где
(где )
)
с дополнительными условиями
 ,
,
 (2)
(2)
 ,
,
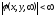 (3)
(3)
Последние два условия вытекают из того, что точечные и линейные заряды отсутствуют, а полный заряд равен нулю. Так как
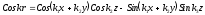 ,
,
задача допускает разделение переменных:
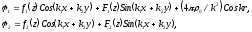
где
последнее слагаемое потенциала
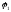 является частным решением уравнения
Пуассона. Функции
является частным решением уравнения
Пуассона. Функции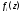 и
и (i=1, 2) удовлетворяют одному и тому же
уравнению:
(i=1, 2) удовлетворяют одному и тому же
уравнению:
 ,
,
в
котором
 .
Принимая во внимание условие (3), находим
.
Принимая во внимание условие (3), находим
 .
.
Постоянные множители ai, bi (i=1, 2) определяются из граничных условий (2), так что
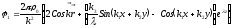 ,
,
 .
.
3.2. Вывести закон Ленгмюра для плоского вакуумного диода:
j=kU3/2,
где j — величина плотности тока, U — напряжение между анодом и катодом, k — коэффициент пропорциональности, зависящий от l — расстояния между катодом и анодом, e, m — заряда и массы электрона. Считать, что сила тока далека от насыщения. начальная скорость электронов равна нулю.
3.3.
Определить потенциал
 и напряженность
и напряженность электрического поля на оси тонкого
диска радиуса R, равномерно заряженного
с поверхностной плотностью
электрического поля на оси тонкого
диска радиуса R, равномерно заряженного
с поверхностной плотностью .
Убедиться, что на большом расстоянии
от диска найденный потенциал совпадает
с кулоновским, а при переходе через
поверхность диска напряженность
электрического поля удовлетворяет
необходимому граничному условию:
.
Убедиться, что на большом расстоянии
от диска найденный потенциал совпадает
с кулоновским, а при переходе через
поверхность диска напряженность
электрического поля удовлетворяет
необходимому граничному условию:
 .
.
3.4.
Вычислить напряженность поля
 и потенциал
и потенциал ,
создаваемый длинным прямым проводником
радиуса а, равномерно заряженным с
плотностью заряда
,
создаваемый длинным прямым проводником
радиуса а, равномерно заряженным с
плотностью заряда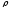 .
.
3.5.
Бесконечная плоская плита толщиной а
равномерно заряжена с плотностью
 .
Найти потенциал
.
Найти потенциал и напряженность
и напряженность электрического поля внутри и вне плиты.
Задачу решить двумя способами:
электрического поля внутри и вне плиты.
Задачу решить двумя способами:
а) используя теорему Гаусса;
б) используя общее решение уравнения Пуассона.
