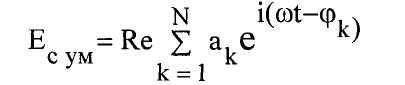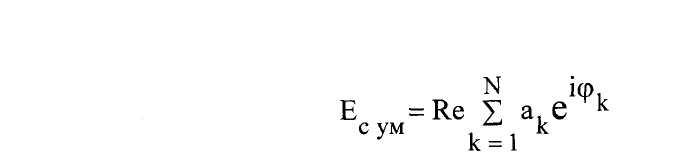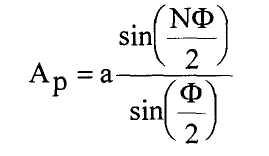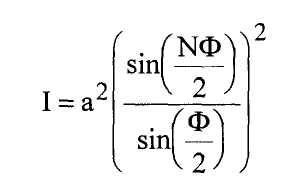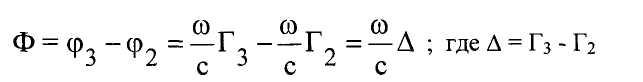Лабораторная работа № 3 исследование дифракционной решетки
Цель работы: ознакомиться с принципом действия и основными характеристиками дифракционных спектральных приборов.
Обеспечивающие средства: набор дифракционных решеток, ртутная лампа, линза, микрометрический окуляр.
Теоретическая часть
Приборы, разлагающие излучение в спектр, называются спектральными приборами. Наибольшее распространение в настоящее время получили дифракционные спектральные приборы. Основным элементом таких приборов является дифракционная решетка, которая позволяет развести излучения с различными длинами волн на разные углы.
Для того, чтобы понять принцип действия дифракционных решеток, рассмотрим распределение интенсивности света на экране при интерференции от N одинаковых точечных источников электромагнитных волн.
Предположим, что все источники излучают монохроматические электромагнитные волны с частотой ω и амплитудой а
|
|
(1) |
где гi - расстояние от i - того источника до точки наблюдения на экране
|
|
(2) |
φi - фаза колебаний электромагнитной волны в точке наблюдения Р (см. рис. 1). Какова будет освещенность экрана?
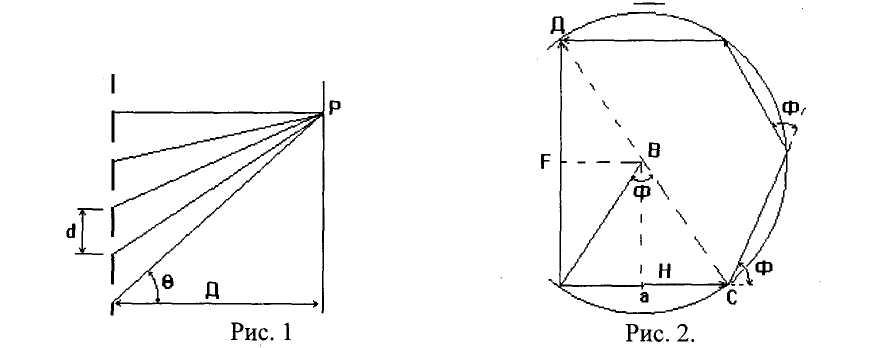
Для того чтобы рассчитать распределение интенсивности на экране, рассмотрим некоторую точку Р экрана и просуммируем амплитуды всех электромагнитных волн, пришедших от N источников, с учетом фазы колебания
|
|
(3) |
Так как нас интересует стационарная (не зависящая от времени картина, то достаточно вычислить сумму (3) для момента времени t=0. Тогда выражение (3) примет вид :
|
|
(4) |
 Как
известно, слагаемое типа
eiφk
есть вектор
длиной ак,
составляющий
угол φк
с
некоторой
осью отсчета. Если расстояние между
источниками
одинаково и равно
d,
а расстояние между крайними источниками
много меньше расстояния до
экрана (Nd«Д),
то разность фаз колебаний Ф = φк
- фк-1-|
электромагнитных волн
от двух произвольных соседних источников
будет одинакова. Тогда, для вычисления
суммы (4), применив
обычное
правило сложения векторов,
получим
(рис.
2), что суммарная амплитуда вектора
электрического поля в точке наблюдения
Р равна вектору АД, длину которого
обозначим Ар.
Интенсивность в
точке
света наблюдения Р определяется
квадратом
амплитуды электромагнитной
волны :
Как
известно, слагаемое типа
eiφk
есть вектор
длиной ак,
составляющий
угол φк
с
некоторой
осью отсчета. Если расстояние между
источниками
одинаково и равно
d,
а расстояние между крайними источниками
много меньше расстояния до
экрана (Nd«Д),
то разность фаз колебаний Ф = φк
- фк-1-|
электромагнитных волн
от двух произвольных соседних источников
будет одинакова. Тогда, для вычисления
суммы (4), применив
обычное
правило сложения векторов,
получим
(рис.
2), что суммарная амплитуда вектора
электрического поля в точке наблюдения
Р равна вектору АД, длину которого
обозначим Ар.
Интенсивность в
точке
света наблюдения Р определяется
квадратом
амплитуды электромагнитной
волны :
|
|
|
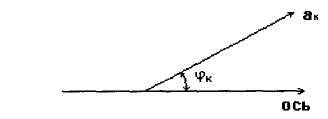
Выразим величину Ар через амплитуды электромагнитных волн источников ак . Так как разность фаз колебаний Ф одинакова, то концы векторов образуют (рис. 2) правильный многоугольник, вокруг которого можно описать окружность радиуса R с центром в некоторой точке В. Легко показать, что угол ABC = Ф, а следовательно, угол АВД = N Ф. Тогда
|
|
|
В то же время из Δ АВН получим : R = 0,5а / sin(Ф/2). Следовательно, суммарная амплитуда равна
|
|
|
а интенсивность
|
|
(5) |
где Ф - разность фаз электромагнитных колебаний от соседних источников.
Графики
функции (5) в зависимости от Ф/2 имеют
следующий вид :
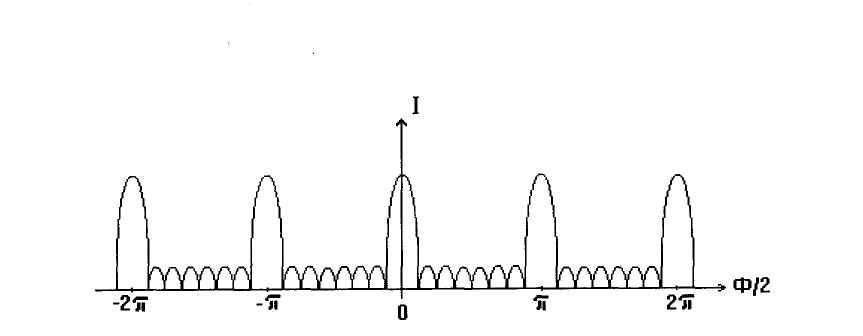
то есть в точках Ф/2 = кπ, где к = 0,1,2,... образуются так называемые главные максимумы, интенсивность света в которых пропорциональна квадрату числа источников. Целое число к называют порядком максимума. Между главными максимумами в точках Ф/2 = ((2k+1)/N) • π/2 образуются побочные максимумы, интенсивность которых почти в 100 раз меньше интенсивности центральных максимумов. Кроме того, как видно из (5), в точках Ф/2 = mπ/N (m =1,2,...,N-1) интенсивность света равна нулю.
Какова разность фаз колебаний от соседних источников в точке наблюдения Р?
Рассмотрим, например, второй и третий источники (рис. 1); по определению
|
|
|
Из рис. 1. видно, что Δ = d sinΘ, тогда
|
|
(6) |
Угол θ однозначно задает положение точки Р на экране, следовательно, на экране будет наблюдаться неравномерное распределение освещенности. Максимум света будет в точках, для которых выполняется условие :
|
|
(7) |