§ 10. Линейное неоднородное уравнение с постоянными коэффициентами

Рассмотрим линейное неоднородное уравнение

, (1)

где и– заданные постоянные коэффициенты.

Нам уже известно, что общее решение такого уравнения складывается из общего решения , соответствующего однородного уравнения

(2)

и какого-нибудь частного решения уравнения (1), т.е.. (3)

Как строить общее решение однородного уравнения (2), мы рассмотрим в предыдущем параграфе. Поэтому теперь вопрос об общем решении уравнения (1) сведен лишь к вопросу о построении хотя бы какого-нибудь частного решенияуравнения (1). Вообще говоря,можно, например, угадать. Но такой способ определенияочень ненадежен. Мы укажем сейчас точные способы, которые всегда приводят к цели.

А. Правая часть уравнения (1) имеет специальный вид

Рассмотрим функцию: , (4)

где – полиномы, а числаm и n – вещественные любые.

По виду этой функции составим «контрольное число» .

Пусть корни характеристического уравнения будут и.

Определим число k следующим образом:

1. , если контрольное число не совпадает ни с одним из корней ;

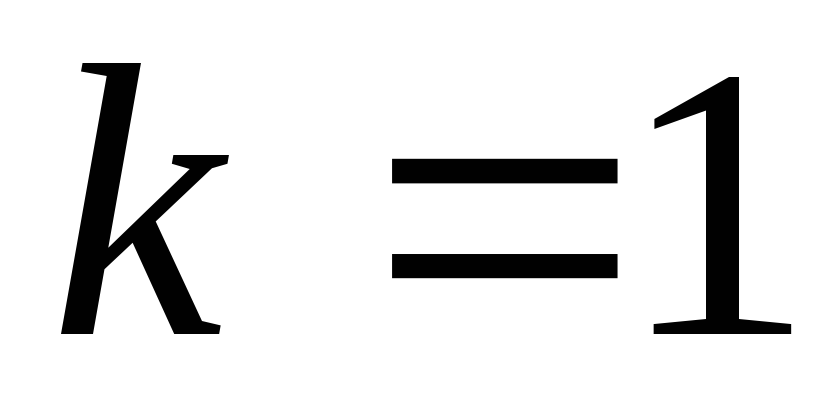2. , если 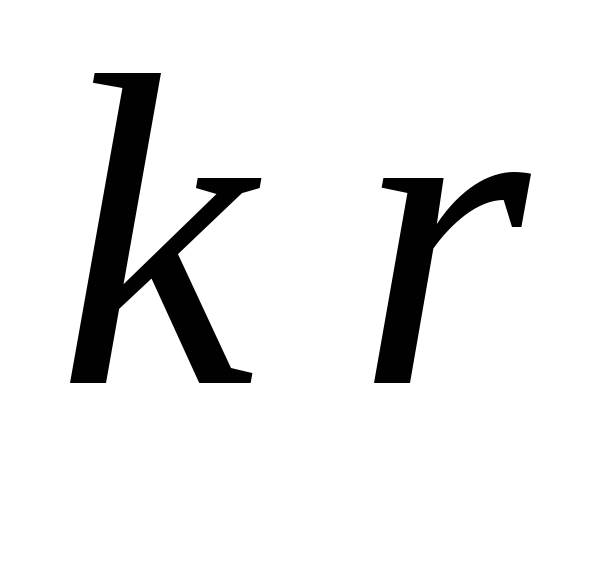совпадает с одним из корней;

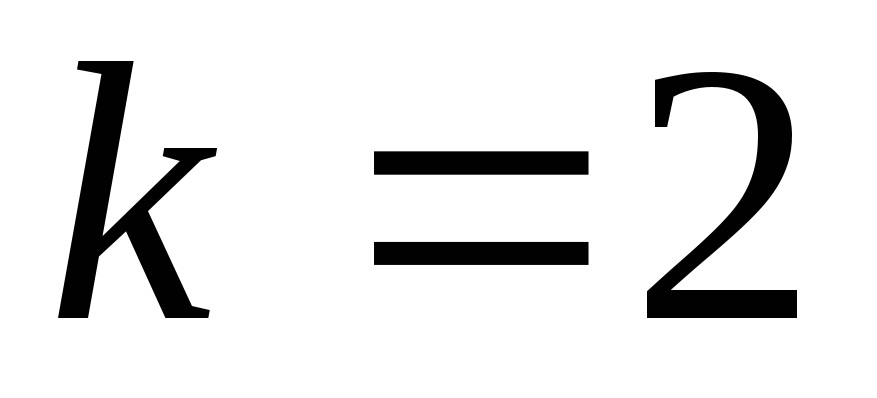3. , если .

Правило. Если правая часть уравнения (1) имеет вид:

(5),

то частное решение следует искать в форме

(6),

где и– полиномы степени, равной наивысшей из степеней полиномови.

Схема нахождения :

1. зная вид , записываютв форме (3), причем полиномы иизаписываются с неопределенными коэффициентами;

2. подставляют в уравнение (1) вместоy, и приравнивают коэффициенты при одинаковых функциях справа и слева. Получают систему уравнений для коэффициентов многочленов . Решая эту систему, находят неизвестные коэффициенты.

3. Найденные коэффициенты подставляют в формулу (3) и находят .

Замечания:

1. Если функция имеет вид: или,то частное решениевсе равно ищется в виде (6).

2. Если , то. В этом случае частное решение ищется в форме:. При этом степеньравна степении.

3. Если , то, аимеет вид.

Пример.

Здесь:

Характеристическое уравнение . Следовательно,.

Поэтому следует искать в виде:

Отсюда Подставляя в уравнениеи, находим:

Отсюда или

.

Следовательно, .

В. Метод вариации произвольных постоянных

В пункте А был изложен метод построения для специального вида. Метод вариации произвольных постоянных применим для функциилюбого вида.

Итак, рассмотрим уравнение (1): , где– любая функция (непрерывная).

Пусть нам известно общее решение однородного уравнения (2)

(7)

где – произвольные постоянные, аи– частные решения уравнения (2).

Будем искать частное решение уравнения (1) в виде , (8)

т.е. в таком же виде, как общее решение (7), но только вместо произвольных постоянных подставим пока неизвестные функции. Найдем их. Поскольку должно быть решением уравнения (1), то функцииисвязаны только одной зависимостью. Для того чтобы их найти, этого недостаточно. Поэтому мы вправе наложить на них еще одно условие по произволу.

Найдем производную .(9)

Потребуем, чтобы имело бы такой же вид, как если быибыли бы постоянными. Отсюда следует, что должно быть

. (10)

Тогда . (11)

Найдем .(12)

Подставляя иопределенные формулами (9), (11) и (12), в уравнение (1), тогда получим:

или .

Но исуть решения однородного уравнения (2), поэтому имеем

(13)

Таким образом, иопределяются из (10) и (13), т.е. из системы уравнений

(14)

Эта неоднородная система линейных алгебраических уравнений относительно ис определителем.

Это определитель Вронского, по доказанному ранее , поэтому система (14) имеет единственное решение. Определение из (14)иинтегрируя их, найдеми, а затем и.

Замечание. Если при интегрировании иввести произвольные постоянные, то сразу получим общий интеграл неоднородного уравнения (1).

Пример.

Соответствующее однородное

Характеристическое уравнение .

Общее решение однородного уравнения

Частное решение заданного уравнения ищем в виде , гдеиопределяются из системы:

Отсюда

Общее решение будет

или .

24