
- •Дифференциальные уравнения
- •§1. Общие понятия
- •§2. Дифференциальные уравнения I порядка
- •Задача Коши.
- •§3. Уравнения с разделяющимися переменными.
- •А. Уравнение с разделенными переменными Уравнением с разделенными переменными называется уравнение вида:
- •§4. Однородные уравнения.
- •§5. Линейные уравнения
- •А. Интегрирование линейного однородного уравнения
- •§6. Уравнение Бернулли
- •§ 7. Теорема существования и единственности решения дифференциального уравнения Условие Липшица
- •Теорема существования и единственности
- •§ 8. Частные случаи уравнений II порядка
- •§ 9. Линейное однородное уравнение с постоянными коэффициентами
- •§ 10. Линейное неоднородное уравнение с постоянными коэффициентами
- •А. Правая часть уравнения (1) имеет специальный вид
- •В. Метод вариации произвольных постоянных
§ 7. Теорема существования и единственности решения дифференциального уравнения Условие Липшица
Р ассмотрим
функцию
ассмотрим
функцию![]() ,
определенную и непрерывную в прямоугольнике
К:
,
определенную и непрерывную в прямоугольнике
К:![]()
Определение.
Если для любого
![]() и любых двух значений
и любых двух значений![]() и
и![]() переменной
переменной![]() :
:
![]() ,
существует такое, не зависящее от х
число
,
существует такое, не зависящее от х
число
![]() ,
что выполнено неравенство:
,
что выполнено неравенство:![]() (1),
то говорят, что функция
(1),
то говорят, что функция![]() в области К удовлетворяет условию
Липшица с постояннойL.
в области К удовлетворяет условию
Липшица с постояннойL.
Замечания:
1.
Если
![]() в области К имеет непрерывную частную
производную
в области К имеет непрерывную частную
производную![]() ,
то всегда найдется такоеL,
что условие (1) будет выполнено.
Действительно, тогда по формуле Лагранжа
,
то всегда найдется такоеL,
что условие (1) будет выполнено.
Действительно, тогда по формуле Лагранжа
![]() (2),
(2),
![]() –лежит
между
–лежит
между
![]() и
и![]() .
.
В
силу непрерывности
![]() в К и замкнутости области К,
в К и замкнутости области К,![]() в К ограничена, т.е.
в К ограничена, т.е.![]() ,
гдеL
– некоторая константа. В этом случае,
в частности, за L
можно принять
,
гдеL
– некоторая константа. В этом случае,
в частности, за L
можно принять
![]() .
.
2.
Условие Липшица (1) более слабое, чем
существование частной производной
![]() ,
так как оно может быть выполнено и в том
случае, когда
,
так как оно может быть выполнено и в том
случае, когда![]() существует не всюду в К.
существует не всюду в К.
Примеры:
Определить, удовлетворяет ли условию Липшица функция
 заданная в прямоугольнике
заданная в прямоугольнике ?
?
Р ешение.
ешение.
![]()
Следовательно,
за L
можно принять
![]() и условие Липшица выполнено. Тот же
результат получим, если используем
замечание 1. Действительно, функция
и условие Липшица выполнено. Тот же
результат получим, если используем
замечание 1. Действительно, функция![]() имеет непрерывную
имеет непрерывную![]() ,
поэтому заL
можно принять
,
поэтому заL
можно принять
![]() .
.
Таким образом, заданная функция удовлетворяет условию Липшица в любом конечном прямоугольнике.
То же самое для функции
 .
.
![]()
Это
значит, что в прямоугольнике K
условие выполнено с
![]() .
.
Здесь константа L не зависит от размеров прямоугольника, следовательно, условие Липшица удовлетворяется на всей плоскости.
То же для функции

![]()
В
то же время
![]() не существует при
не существует при![]() ,
т.к.
,
т.к.
![]() .
.
Теорема существования и единственности
Теорема (Коши)
Пусть
![]() удовлетворяет условиям:
удовлетворяет условиям:
1)
непрерывна в прямоугольнике K:
![]() ,
тогда вK
,
тогда вK
![]() ограничена, то найдется такое
ограничена, то найдется такое![]()
![]() (3)
(3)
удовлетворяет в K условию Липшица
![]() (4)
(4)
Т огда
в интервале:
огда
в интервале:![]() (5)
(5)
дифференциальное
уравнение
![]() (6)
(6)
обладает
единственным решением
![]() ,
таким, что
,
таким, что![]() .
.
Замечания:
Для существования решения достаточно непрерывности
 вK.
вK.Для единственности решения требуется выполнение условия Липшица (4), которое может быть заменено более жестким условием существования в K непрерывной
 .
.При доказательстве теоремы рассматривается задача Коши:
 , (7)
, (7)
которая
заменяется эквивалентным ей интегральным
уравнением
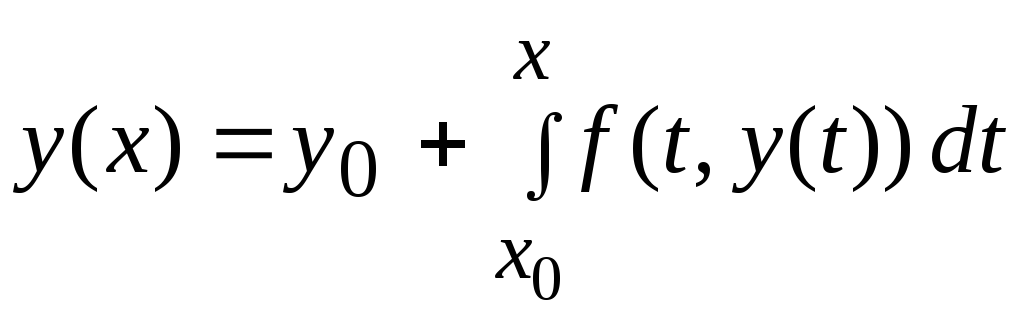 . (8)
. (8)
Затем
к уравнению (8) применяется так называемый
метод последовательных приближений
Пикара. Он состоит в том, что строится
последовательность функций
![]() сходящаяся к решению уравнения (8).
Функции
сходящаяся к решению уравнения (8).
Функции![]() строятся по следующему правилу: за
исходное приближение принимается
строятся по следующему правилу: за
исходное приближение принимается![]() ,
а следующие вычисляются по формуле:
,
а следующие вычисляются по формуле: . (9)
. (9)
Это есть рабочая формула для построения приближенного решения по методу последовательных приближений.
Д
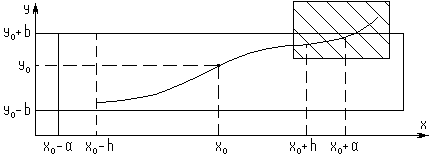 опустим
интегральная кривая построена на
интервале
опустим
интегральная кривая построена на
интервале .
Возьмем конечную точку за центр нового
прямоугольника и продолжим решение
вправо. Поступая так, каждый раз, можно
продолжить решение (интегральную
кривую) до самой границы областиG
задания функции
.
Возьмем конечную точку за центр нового
прямоугольника и продолжим решение
вправо. Поступая так, каждый раз, можно
продолжить решение (интегральную
кривую) до самой границы областиG
задания функции
 (в предположении, чтоG
конечна и замкнута).
(в предположении, чтоG
конечна и замкнута).
Мы
построили интегральную кривую, проходящую
через точку
![]() .
Можно выбрать любую другую точку и опять
получим единственную интегральную
кривую. Таким образом, областьG
как бы состоит из интегральных кривых.
.
Можно выбрать любую другую точку и опять
получим единственную интегральную
кривую. Таким образом, областьG
как бы состоит из интегральных кривых.
Т еорема.
Если
еорема.
Если
![]() определена и непрерывна на всей плоскости
и удовлетворяет условию Липшица во
всякой конечной области этой плоскости,
то всякая интегральная кривая при
возрастании или продолжима до
определена и непрерывна на всей плоскости
и удовлетворяет условию Липшица во
всякой конечной области этой плоскости,
то всякая интегральная кривая при
возрастании или продолжима до![]() или имеет вертикальную асимптоту при
конечном значении
или имеет вертикальную асимптоту при
конечном значении![]() ,
т.е. интегральная кривая не может
окончится где-то внутри области.
,
т.е. интегральная кривая не может
окончится где-то внутри области.
Пример.
![]() .
.
Здесь
![]() удовлетворяет всем условиям теоремы.
Решением задачи Коши
удовлетворяет всем условиям теоремы.
Решением задачи Коши![]() будет
будет![]() .
Решение имеет вертикальные асимптоты
.
Решение имеет вертикальные асимптоты![]() .
.
Те точки области G, в которых функция
 неопределена или перестает быть
непрерывной или не выполняется условие
Липшица, называются особыми точками
уравнения
неопределена или перестает быть
непрерывной или не выполняется условие
Липшица, называются особыми точками
уравнения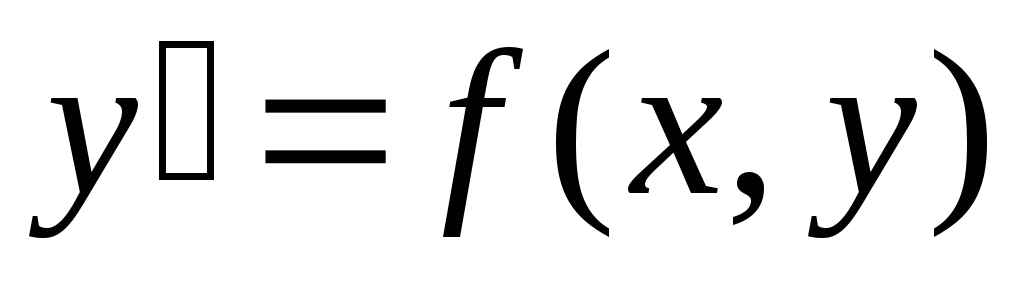 .
Таким образом, особые точки это те
точки, в которых нарушаются условия
теоремы существования и единственности.
Особые точки могут быть изолированными,
а могут составлять и целые области.
.
Таким образом, особые точки это те
точки, в которых нарушаются условия
теоремы существования и единственности.
Особые точки могут быть изолированными,
а могут составлять и целые области.
