
- •1.2. Лекция 2. Скалярное, векторное и смешанное
- •Скалярное произведение
- •Геометрические свойства скалярного произведения
- •Алгебраические свойства скалярного произведения
- •Векторное произведение
- •Смешанное произведение
- •Двойное векторное произведение
- •Решение векторных уравнений
- •Законы физики и векторный язык
Векторное произведение
Ориентация тройки векторов. Упорядоченная тройка некомпланарных векторов называется правой (левой), если из конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки (по часовой стрелке). Начала векторов тройки предполагаются при этом совмещенными. Очевидно, любая тройка некомпланарных векторов является либо правой, либо левой.
Векторное произведение. Векторным произведением вектора a на вектор b называется вектор c , удовлетворяющий трем условиям:
1)
![]() ,
,
![]() ,
,
2)
![]() и
и
![]() ,
,
3) если a
не параллелен
![]() ,
то тройка векторов
,
то тройка векторов
![]() правая. Векторное произведение (рис. 5)
векторовa
и b
обозначают
правая. Векторное произведение (рис. 5)
векторовa
и b
обозначают
![]() или
или![]() .
Мы будем придерживаться первого
обозначения.
.
Мы будем придерживаться первого
обозначения.

Рис. 5. Векторное произведение
Понятие векторного
произведения родилось в механике. Момент
силы F,
приложенной к точке
![]() ,
относительно точки
,
относительно точки![]() равен векторному произведению
равен векторному произведению
![]() .
.
Геометрические свойства векторного произведения. Из определения векторного произведения нетрудно получить следующие свойства:
1.
![]() .
.
2. Модуль векторного произведения равен площади параллелограмма, построенного на векторах, приведенных к общему началу.
Докажем свойство
2). Для площади
![]() параллелограмма имеем
параллелограмма имеем
![]() ,
что и требовалось.
,
что и требовалось.
Алгебраические свойства векторного произведения. К таковым относят следующие свойства:
1)
![]() – антикоммутативность;
– антикоммутативность;
2)
![]() – однородность;
– однородность;
3)
![]() – дистрибутивность;
– дистрибутивность;
4)
![]() – идемпотентность.
– идемпотентность.
Свойства 1, 2, 4 легко следуют из определения. Свойство 3 нуждается в доказательстве; мы получим его после введения базиса.
Получим на векторном
языке выражение для площади параллелограмма
![]() ,
построенного на векторахa
и b,
приведенных к общему началу. С одной
стороны,
,
построенного на векторахa
и b,
приведенных к общему началу. С одной
стороны,
![]() .
С другой -
.
С другой -
![]() .
.
Или
 .
(2.15)
.
(2.15)
Таким образом,
 .
(2.16)
.
(2.16)
Определитель в правой части формулы (2.16) называется определителем Грама пары векторов a,b.
Полученный результат можно переписать в виде
![]() .
.
Докажем известную
со школы теорему синусов.
Рассмотрим треугольник из векторов
таких, что
![]() .
Помножим векторно на
.
Помножим векторно на![]() обе части этого равенства:
обе части этого равенства:
![]() .
.
Так как
![]() ,
то
,
то
![]() .
Отсюда
.
Отсюда
![]() ,
,
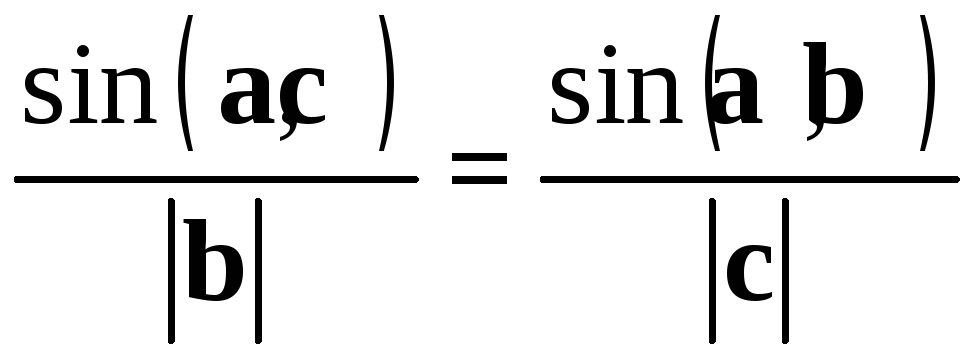 ,
,
что и требовалось.
Смешанное произведение
Смешанное произведение есть тернарная, т.е. трехместная, операция, в отличие, например, от двухместной операции скалярного произведения. Смешанное произведение (и это оправдывает название) определяется через векторное и скалярное произведения.
Смешанным
произведением трех векторов
![]() называется число
называется число
![]() .
.
Смешанное
произведение имеет четкий геометрический
смысл.
Ориентированным объемом параллелепипеда,
построенного на упорядоченной тройке
векторов
![]() ,
приведенных к общему началу, называется
число, обозначаемое
,
приведенных к общему началу, называется
число, обозначаемое
![]() и равное
объему этого параллелепипеда, взятому
со знаком "плюс", если эта тройка
правая, и со знаком "минус" – в
противном случае.
и равное
объему этого параллелепипеда, взятому
со знаком "плюс", если эта тройка
правая, и со знаком "минус" – в
противном случае.
Лемма.
![]() .
.
Доказательство.
Объем параллелепипеда (рис.6) равен
произведению площади его основания
![]() на высоту
на высоту![]() .
.
Поэтому
![]() .
.
Теперь вместо
![]() .
Можно писать
.
Можно писать![]() .
.

Рис. 6. Смешанное произведение
Следствие 1.
![]() .
.
Следствие 2.
Три вектора
![]() компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда![]() .
.
Предложение.
Если вектора
![]() некомпланарные, то и вектора
некомпланарные, то и вектора
![]() некомпланарные.
некомпланарные.
Доказательство. Предположим
![]()
и, например,
![]() .
Умножив обе части равенства скалярно
на
.
Умножив обе части равенства скалярно
на![]() ,
мы получим
,
мы получим![]() ,
что противоречит некомпланарности
векторов базиса.
,
что противоречит некомпланарности
векторов базиса.
