1.7 Лекция 7. Поверхности второго порядка

Уравнение поверхности второго порядка. Цилиндры. Конусы. Эллипсоиды, гиперболоиды и параболлоиды. Канонические уравнения. Приложения в оптике.

Определение 7.1 Поверхностью второго порядка называется множество всех точек пространства, удовлетворяющих уравнению

Уравнение любой поверхности второго порядка невырожденным линейным преобразованием неизвестных можно привести к каноническому виду. Каноническое уравнение не содержит произведений неизвестных , , . Кроме того, если каноническое уравнение содержит квадрат неизвестной, то первая степень этой неизвестной в уравнение не входит.

За исключением вырожденных случаев (плоскости, точки, пустое множество), существует девять типов поверхностей второго порядка:

– эллипсоид,

– однополостный гиперболоид,

– двуполостный гиперболоид,

– конус,

– эллиптический параболоид,

– гиперболический параболоид,

– эллиптический цилиндр,

– гиперболический цилиндр,

– параболический цилиндр.

Каноническое уравнение эллипсоида имеет вид

.

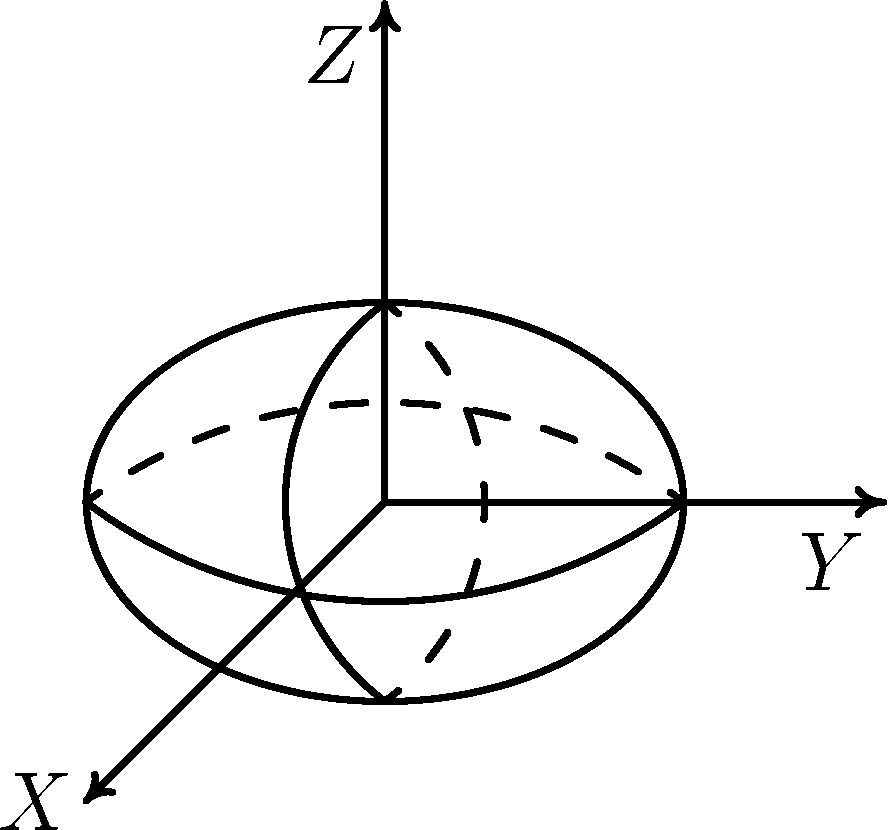
Рис.1. Эллипсоид

Определение 7.2 Положительные числа , , называются полуосями эллипсоида.

Если , или , или , то эллипсоид образован вращением эллипса вокруг одной из координатных осей. При эллипсоид является сферой. Сечения эллипсоида плоскостями , , являются эллипсами

,

вырождающимися в точки при . Аналогичный результат имеем при рассмотрении сечений эллипсоида плоскостями и .

Однополостный гиперболоид имеет каноническое уравнение

.

Рис.2. Однополостной гиперболоид

Горизонтальные плоскости пересекают гиперболоид по эллипсам

при любом значении . Вертикальные плоскости и пересекают однополостный гиперболоид, соответственно, по гиперболам

и .

В зависимости от знака правой части уравнений направление ветвей гипербол изменяется, в случае равенства правой части нулю получим уравнения пересекающихся прямых. При условии однополостный гиперболоид образуется вращением гиперболы относительно оси аппликат. Однополостный гиперболоид является линейчатой поверхностью: через каждую его точку проходят две пересекающиеся прямые, лежащие на гиперболоиде.

Двуполостной гиперболоид имеет каноническое уравнение

.

Заметим, что горизонтальные плоскости пересекают двуполостный гиперболоид лишь при условии . В отличие от однополостного гиперболоида, прямолинейных образующих двуполостный гиперболоид не имеет.

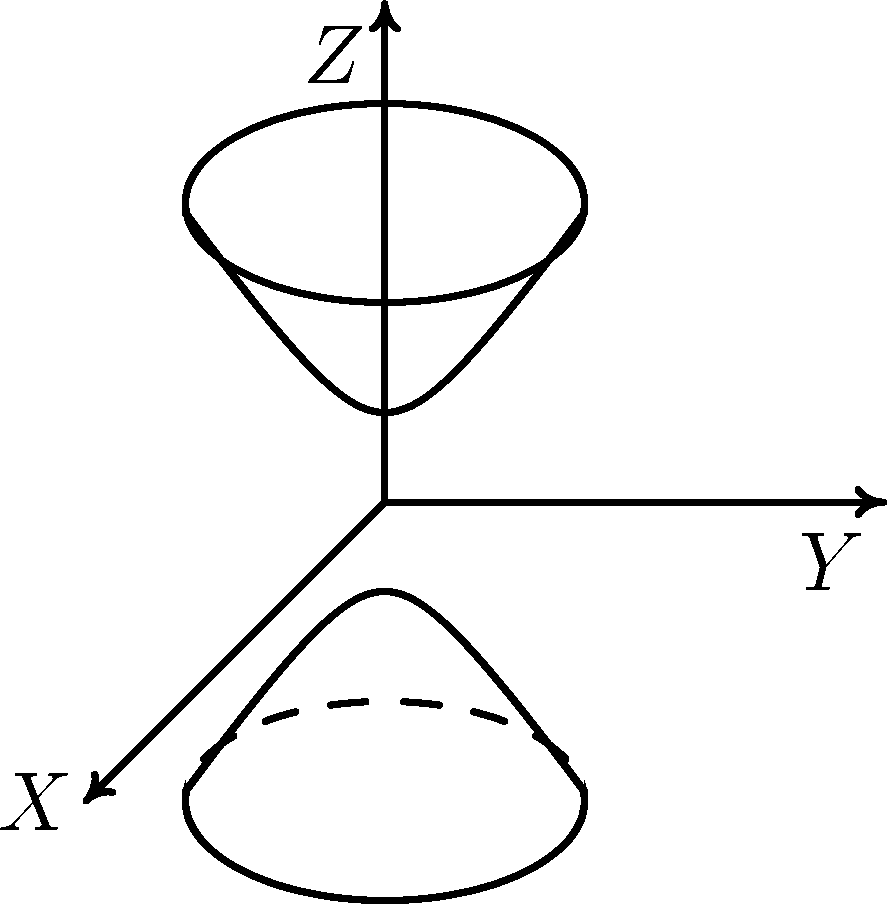
Рис. 3. Двуполостной гиперболоид

Конус имеет каноническое уравнение

и при является конусом вращения, или круговым конусом.

Рис.4. Конус

Координатные плоскости и пересекают конус, соответственно, по прямым

, .

Интересно, что при сечении конуса различными плоскостями получаются все типы невырожденных линий второго порядка: эллипсы, гиперболы и параболы.

Эллиптический параболоид имеет каноническое уравнение

.

Горизонтальные сечения эллиптического параболоида плоскостями – эллипсы, вертикальные сечения – параболы. При условии эллиптический параболоид является поверхностью вращения.

Рис.5. Эллиптический параболоид

Гиперболический параболоид имеет каноническое уравнение

.

Горизонтальные сечения этой поверхности – гиперболы с различным направлением ветвей и пересекающиеся прямые в плоскости XOY. Вертикальные сечения, параллельные координатным плоскостям, – параболы. Как и однополостный гиперболоид, эта поверхность является линейчатой, т.е. имеет прямолинейные образующие.

Рис. 6. Гиперболический параболоид

Канонические уравнения цилиндрических поверхностей содержат только две переменные, и . Следовательно, сечения цилиндрических поверхностей плоскостями одинаковы и не зависят от значения . Цилиндрические поверхности второго порядка задаются следующими каноническими уравнениями:

Рис.7. Эллиптический цилиндр

Каноническое уравнение эллиптического цилиндра

.

Рис.8. Гиперболический цилиндр

Каноническое уравнение гиперболического цилиндра

.

Рис. 9. Параболический цилиндр

Каноническое уравнение параболического цилиндра

.

Вопросы для самопроверки

1. Что называется поверхностью второго порядка?

2. Какие основные типы невырожденных поверхностей второго порядка?

3. Каковы канонические уравнения эллипсоида, одно и двуполостного гиперболоидов?

4. Каковы канонические уравнения конуса, эллиптического и гиперболического параболоидов?

5. Каковы канонические уравнения цилиндрических поверхностей?

47