
Analiticheskaya_geom / 1_3_Vektory_v_koordinatakh_Ortonormirovanny_ba
.doc1.3. Лекция 3. Векторы в координатах.
Ортонормированный базис
Базис и координаты. Координатные столбцы векторов. Линейные операции над векторами в координатной форме. Ортонормированный базис. Направляющие косинусы. Скалярное произведение в ортонормированном базисе. Детерминанты второго и третьего порядков. Векторное и смешанное произведения в правом ортонормированном базисе.
В лекции 2 вместо векторов-сил, векторов-скоростей и т.д. мы рассматривали идеальные объекты – свободные геометрические векторы. Это был первый шаг абстрагирования: от физических объектов к геометрическим. В этой главе мы сделаем второй шаг: от геометрических объектов к алгебраическим. Благодаря этому мы получим возможность считать! Действительно, попробуйте-ка сложить по правилу параллелограмма три некомпланарных вектора или, что несравненно сложнее, решить векторное уравнение. Но плата за эту возможность оказывается довольно высока, что будет ясно с позиций тензорного исчисления.
Базис и координаты
Базисом на прямой называется любой ненулевой вектор на этой прямой.
Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов этой плоскости.
Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов.
Представление вектора в виде линейной комбинации некоторых векторов называют его разложением по этим векторам. Как правило, рассматривают разложение вектора по базису.
Если
![]() базис в пространстве и
базис в пространстве и
![]() ,
,
то числа
![]() ,
,
![]() ,
,![]() называют координатами
вектора
называют координатами
вектора
![]() в базисе
в базисе
![]() .
.
Теорема 3.1.
Пусть
![]() – базис в пространстве.
Тогда любой вектор
– базис в пространстве.
Тогда любой вектор
![]() допускает, притом единственное,
представление вида
допускает, притом единственное,
представление вида
![]() .
(3.1)
.
(3.1)
Доказательство. Докажем единственность представления (3.1). Допустим, существует другое представление:
![]() .
.
Тогда
![]() .
.
Умножим это
равенство скалярно на вектор
![]() .
Получим
.
Получим
![]() .
.
Так как
![]() ,
то
,
то
![]() .
Аналогично заключаем, что
.
Аналогично заключаем, что
![]() ,
,
![]() .
Единственность представления (3.1)
доказана.
.
Единственность представления (3.1)
доказана.
Возможность
представления (3.1)
доказывается
несложным геометрическим построением.
Приведем вектора
![]() ,
,![]() ,
,![]() ,
,![]() к общему началу
к общему началу
![]() .
Для простоты предположим, что вектор
.
Для простоты предположим, что вектор
![]() образует острые углы со всеми векторами
образует острые углы со всеми векторами
![]() ,
,![]() ,
,![]() .
Вообразим себе параллелепипед, выходящие
из точки
.
Вообразим себе параллелепипед, выходящие
из точки
![]() ребра которого суть продолженные вектора
ребра которого суть продолженные вектора
![]() ,
,![]() ,
,![]() ,
а большая диагональ, выходящая из точки
,
а большая диагональ, выходящая из точки
![]() ,
– вектор
,
– вектор
![]() .
Тогда
.
Тогда
![]() равен сумме указанных векторов,
представляющих названные ребра.
равен сумме указанных векторов,
представляющих названные ребра.
Координатные столбцы векторов
Пусть
![]() – базис в пространстве и
– базис в пространстве и
![]() ,
,
![]() .
.
Столбцы
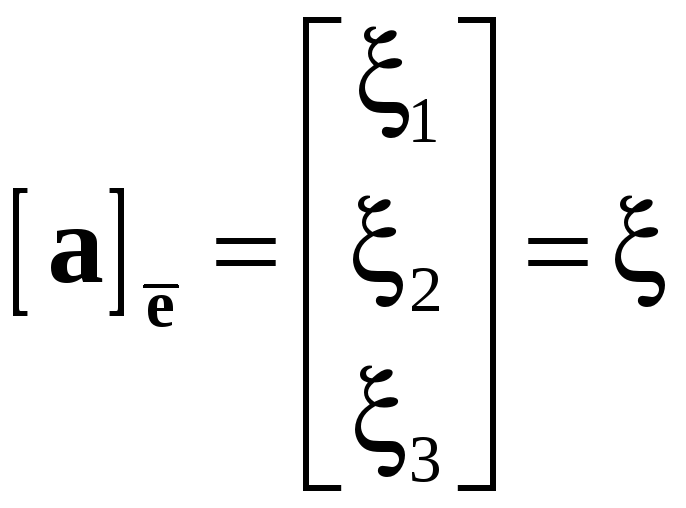 ,
,
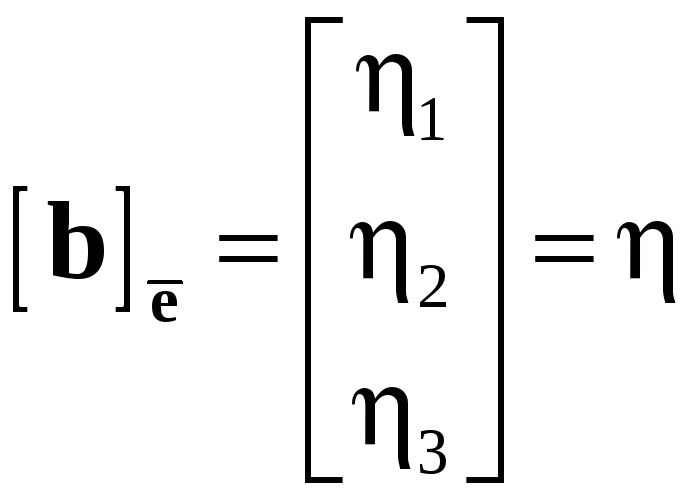
будем называть
координатными
столбцами
векторов
![]() ,
,
![]() в базисе
в базисе
![]() .
Множество всех таких столбцов обозначим
через
.
Множество всех таких столбцов обозначим
через
![]() .
Отображение
.
Отображение
![]() ,
(3.2)
,
(3.2)
как следует из
предыдущей теоремы, устанавливает (при
фиксированном базисе) взаимно однозначное
соответствие между множеством
![]() всех свободных векторов и множеством
всех свободных векторов и множеством
![]() .
Это отображение, оказывается, обладает
чрезвычайно важной особенностью –
является изоморфизмом.
Обсудим это.
.
Это отображение, оказывается, обладает
чрезвычайно важной особенностью –
является изоморфизмом.
Обсудим это.
Из алгебраических свойств линейных операций над векторами следует
![]() .
.
Тогда
 (3.3)
(3.3)
Аналогично проверяется, что
 .
(3.4)
.
(3.4)
Введем на
![]() операции сложения столбцов и умножения
столбцов на числа:
операции сложения столбцов и умножения
столбцов на числа:
 ,
(3.5)
,
(3.5)
 .
(3.6)
.
(3.6)
Теперь (3.3), (3.4) можно переписать в виде
![]() ,
,
![]() .
(3.7)
.
(3.7)
Иными словами,
отображение
![]() удовлетворяет условиям:
удовлетворяет условиям:
![]() ,
,
![]() ,
(3.8)
,
(3.8)
т. е. является изоморфизмом линейных пространств.
Упражнение 3.1. Докажите тождество
![]() .
.
Изоморфизм
![]() позволяет вместо геометрической системы
позволяет вместо геометрической системы
![]() изучать арифметическую систему
изучать арифметическую систему
![]() .
Так, например, (3.5) есть алгебраическое
выражение геометрического правила
параллелограмма сложения векторов.
.
Так, например, (3.5) есть алгебраическое
выражение геометрического правила
параллелограмма сложения векторов.
Ортонормированный базис
Базис
![]() называется ортонормированным,
если
называется ортонормированным,
если

![]() (3.9)
(3.9)
Из определения скалярного произведения следует, что базис ортонормирован тогда и только тогда, когда его вектора имеют единичную длину и попарно ортогональны. Геометрический смысл координат вектора в ортонормированном базисе проясняет следующее
Предложение
3.1. Пусть
![]() – ортонормированный
базис и
– ортонормированный
базис и
![]() .
Тогда
.
Тогда
![]() ,
,
где
![]() ,
т. е.
,
т. е.
![]() есть прямоугольная проекция вектора
есть прямоугольная проекция вектора
![]() на ось вектора
на ось вектора
![]() ,
,
![]() .
.
Доказательство. По определению скалярного произведения
![]() .
.
С другой стороны,
из алгебраических свойств скалярного
произведения и ортонормированности
базиса
![]() следует
следует
![]()
Косинусы
![]() называют направляющими
косинусами
вектора
называют направляющими
косинусами
вектора
![]() .
.
В ортонормированном базисе скалярное произведение имеет очень простой вид.
Теорема 3.2.
Пусть
![]() – ортонормированный
базис и
– ортонормированный
базис и
![]() ,
,
![]() Тогда
Тогда
![]()
Доказательство. Используя алгебраические свойства скалярного произведения, получим
![]() =
=
![]()
![]()
Следствие 3.1.
![]()
Доказательство.
![]()
Следствие 3.2.

Доказательство
следует из определения скалярного
произведения как
![]() и только что полученных координатных
представлений скалярного произведения
и модуля вектора.
и только что полученных координатных
представлений скалярного произведения
и модуля вектора.
Упражнение 3.2. Получите следующую формулу для направляющих косинусов вектора:

![]() .
.
Упражнение 3.3. Докажите тождество для направляющих косинусов вектора
![]() .
.
Вектор, сонаправленный
вектору
![]() и имеющий единичную длину, называется
ортом вектора
и имеющий единичную длину, называется
ортом вектора
![]() и обозначается
и обозначается
![]() .
.
Упражнение
3.4.
Докажите,
что
 и координаты вектора
и координаты вектора
![]() совпадают с направляющими косинусами
вектора
совпадают с направляющими косинусами
вектора
![]() .
.
Предложение
3.2. Если
![]() – правый ортонормированный базис,
то
– правый ортонормированный базис,
то
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Доказательство непосредственно следует из ортонормированности базиса и определений векторного и скалярного произведений.
Обычно используют правый ортонормированный базис.
Теорема 3.3.
Пусть
![]() – правый ортонормированный базис и
– правый ортонормированный базис и
![]() ,
,
![]() Тогда
Тогда
 .
(3.10)
.
(3.10)
Доказательство. Из алгебраических свойств векторного произведения и предложения 3.2 следует
![]()
![]()
![]()
 .
.
Теорема 3.4.
Пусть
![]() – правый ортонормированный базис и
– правый ортонормированный базис и
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
 .
.
Доказательство.
По определению
смешанного произведения
![]() .
Умножая скалярно обе части равенства
(3.10), получим требуемое.
.
Умножая скалярно обе части равенства
(3.10), получим требуемое.
Следствие.
Вектора
![]() ,
,
![]() ,
,
![]() компланарны
тогда и только тогда, когда
компланарны
тогда и только тогда, когда

Вычислив формулу (3.6) из лекции 2 в координатах, получим следующее тождество Лагранжа:
 .
.
Разлагая векторы
![]() ,
,
![]() ,
,
![]() по ортонормированному базису, с помощью
теоремы об умножении определителей
нетрудно получить уже встречавшееся
тождество
по ортонормированному базису, с помощью
теоремы об умножении определителей
нетрудно получить уже встречавшееся
тождество
 .
.
Упражнения
3.1.
Как выглядит множество
![]() точек плоскости, у которых координаты
точек удовлетворяют неравенству
точек плоскости, у которых координаты
точек удовлетворяют неравенству
![]() для некоторого
для некоторого
![]() ?
Как выглядит множество
?
Как выглядит множество
![]() ?
?
3.2.
Найти ортогональную проекцию вектора
![]() на прямую, направление которой определяется
вектором
на прямую, направление которой определяется
вектором
![]() ,
и ортогональную составляющую вектора
,
и ортогональную составляющую вектора
![]() относительно этой прямой. Найти орт
вектора
относительно этой прямой. Найти орт
вектора
![]() и его направляющие косинусы. Сделать
чертеж.
и его направляющие косинусы. Сделать
чертеж.
3.3.
Даны два вектора
![]() и
и
![]() .
Найти вектор
.
Найти вектор
![]() ,
удовлетворяющий системе уравнений
,
удовлетворяющий системе уравнений
![]() ,
,
![]() .
Найти орт вектора
.
Найти орт вектора
![]() и его направляющие косинусы.
и его направляющие косинусы.
3.4.
Векторы
![]() ,
,
![]() и
и
![]() и имеют равные длины и образуют попарно
равные углы. Найти координаты вектора
и имеют равные длины и образуют попарно
равные углы. Найти координаты вектора
![]() ,
если
,
если
![]() ,
,
![]() .
Найти орт вектора
.
Найти орт вектора
![]() и его направляющие косинусы.
и его направляющие косинусы.
3.5.
Даны векторы
![]() ,
,
![]() ,
,
![]() .
Вычислить
.
Вычислить
![]() и
и
![]() .
.
3.6.
Даны вершины треугольника
![]() ,
,
![]() ,
,
![]() .
Вычислить его высоту, опущенную из
вершины
.
Вычислить его высоту, опущенную из
вершины
![]() .
.
3.7.
Раскрыть скобки и упростить
![]() .
.
3.8.
Сила
![]() приложена к точке
приложена к точке
![]() .
Определить момент силы относительно
начала координат, его величину и
направляющие косинусы.
.
Определить момент силы относительно
начала координат, его величину и
направляющие косинусы.
3.9.
Доказать, что площадь выпуклого
многоугольника на плоскости с вершинами
![]() равна половине абсолютной величины
выражения
равна половине абсолютной величины
выражения
 .
.
Вопросы для самопроверки
1. Что такое базис на плоскости и в пространстве?
2. Существует ли
направление в пространстве, составляющее
с осями координат прямоугольной системы,
углы по
![]() градусов?
градусов?
3. Задайте два вектора своими координатами и найдите их скалярное произведение.
4. Задайте детерминанты второго и третьего порядков и вычислите их.
5. Задайте два (три) вектора их координатами и найдите их векторное (смешанное) произведение.
