
Analiticheskaya_geom / 1_1_Vektory_Invariantnaya_teoria
.docРАЗДЕЛ 2 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЛИНЕЙНАЯ АЛГЕБРА
1. МОДУЛЬ I. ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
1.1. Лекция 1. Векторы. Инвариантная теория
Скалярные и векторные величины. Три условия векторности величины. Примеры и контрпримеры. Аксиальные векторы. Формализация: свободные геометрические векторы и операции над ними. Линейные комбинации и линейная зависимость. Коллинеарность и компланарность; их связь с линейной зависимостью.
Вначале будем изучать векторы независимо ни от какой системы координат, т.е. "сами по себе" (термин Иммануила Канта). Иными словами, будем строить инвариантную теорию векторов. Именно такая теория имеет ряд преимуществ при записи физических законов.
Скалярные и векторные величины. Три условия векторности величины. Примеры и контрпримеры. Аксиальные векторы
Сущности, которые при выбранной единице измерения могут быть однозначно заданы числом, называют скалярными величинами. Таковы масса, плотность, время, энергия, температура и т.д. Но в природе есть и более сложные сущности. Например, для задания скорости нужно указать не только ее величину, но и направление. То же можно сказать о силе, ускорении, угловой скорости, повороте... Однако, как будет показано ниже, эти сущности обладают различными алгебраическими свойствами.
Векторными величинами физики договорились называть сущности, которые:
а) однозначно задаются числом (при выбранной единице измерения) и направлением;
б) это направление существует "само по себе", т.е. не зависит ни от каких договоренностей (правило левой руки, правило буравчика, и т.п.);
в) складываются с себе подобными по правилу параллелограмма.
При этом нужно указать, что понимается под сложением двух физических величин, а это не всегда просто.
Самый простой пример векторных величин - силы, приложенные к одной точке.
Обратимся к угловой
скорости. В качестве ее направления
можно взять ось вращения. Но при выборе
направления этой оси остается
неопределенность в
![]() .
Для устранения ее как раз и требуется
договоренность типа "правила
буравчика", а это нарушает условие
б) определения вектора. Условие в)
определения при этом выполняется.
.
Для устранения ее как раз и требуется
договоренность типа "правила
буравчика", а это нарушает условие
б) определения вектора. Условие в)
определения при этом выполняется.
Сущности,
удовлетворяющие условиям а), в), но не
удовлетворяющие условию б), называют
псевдовекторными
величинами или аксиальными
(осевыми)
векторными величинами. Еще сложнее
обстоит дело с поворотами. Под операцией
сложения поворотов естественно понимать
последовательное выполнение поворотов.
Нетрудно указать повороты
![]() ,
,
![]() такие, что
такие, что
![]() ,
т.е. сложение поворотов некоммутативно.
(Возьмите прямоугольный параллелепипед,
например книгу, и поупражняйтесь.) Но
правило параллелограмма коммутативно!
Значит, повороты складываются по иному
правилу. Тем самым для поворотов
нарушается условие в) определения
векторной величины, и они не являются
таковыми.
,
т.е. сложение поворотов некоммутативно.
(Возьмите прямоугольный параллелепипед,
например книгу, и поупражняйтесь.) Но
правило параллелограмма коммутативно!
Значит, повороты складываются по иному
правилу. Тем самым для поворотов
нарушается условие в) определения
векторной величины, и они не являются
таковыми.
Формализация: свободные геометрические векторы. Коллинеарность, компланарность.
Было бы слишком затратно строить отдельно исчисления векторов сил, векторов скоростей и т. д. Несмотря на очевидные различия, у них много общего. Именно эта общность является основанием математической абстракции – введения понятия свободного геометрического вектора.
Направленный
отрезок в пространстве будем называть
свободным
геометрическим вектором.
Два таких вектора считаются равными,
если они могут быть совмещены параллельным
переносом. Очевидно, если вектор
![]() равен вектору
равен вектору
![]() ,
то вектор
,
то вектор
![]() равен вектору
равен вектору
![]() .
Если
.
Если
![]() равен
равен
![]() ,
а
,
а
![]() равен
равен
![]() ,
то
,
то
![]() равен
равен
![]() .
Рассматривают также скользящие
и связанные
векторы. Для них дается другое определение
равенства. В дальнейшем будем рассматривать
только свободные векторы и называть их
просто векторами.
.
Рассматривают также скользящие
и связанные
векторы. Для них дается другое определение
равенства. В дальнейшем будем рассматривать
только свободные векторы и называть их
просто векторами.
Векторы называют коллинеарными, если существует прямая, которой они параллельны. Векторы называют компланарными, если существует плоскость, которой они параллельны. Два вектора всегда компланарны, три – нет. (Проверьте!)
Линейными операциями над векторами называют операции сложения векторов по правилу параллелограмма и умножения векторов на числа, известные из школьного курса. Отметим, что по правилу параллелограмма складываются две силы, приложенные к одной точке, а по известному правилу треугольника - перемещения. (Как обосновываются эти утверждения?) Для свободных векторов эти два правила равносильны, хотя их физические прообразы имеют совершенно разную природу. Это есть достойный удивления факт нашего мира.
Вектор нулевой
длины называется нулевым
вектором и обозначается
![]() .
.
Легко проверить следующие алгебраические свойства линейных операций:
1)
![]() (коммутативность
сложения);
(коммутативность
сложения);
2)
![]() (ассоциативность
сложения);
(ассоциативность
сложения);
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() .
.
Вектор
![]() обозначается
обозначается
![]() .
Разностью
векторов
.
Разностью
векторов
![]() и
и
![]() называется сумма векторов
называется сумма векторов
![]() и
и
![]() .
Она обозначается
.
Она обозначается
![]() .
.
Свойства 1), 2) проиллюстрированы на рис. 1.


Рис.1. Правило параллелограмма. Ассоциативность сложения
Линейные комбинации и линейная зависимость
Выражение вида
![]()
называется линейной
комбинацией векторов
![]() ,
,![]() ,
...,
,
...,
![]() .
Числа
.
Числа![]() ,
,
![]() ,
…,
,
…,
![]() называются ее коэффициентами.
называются ее коэффициентами.
Если вектор
![]() равен линейной комбинации векторов
равен линейной комбинации векторов
![]() ,
,
![]() ,
...,
,
...,![]() ,
то говорят, что вектор
,
то говорят, что вектор
![]() линейно
выражается через
векторы
линейно
выражается через
векторы
![]() ,
,![]() ,
…,
,
…,
![]() .
.
Система векторов
![]() ,
,
![]() ,
...,
,
...,
![]() называется линейно
зависимой, если
существуют числа
называется линейно
зависимой, если
существуют числа
![]() ,
,
![]() ,
…,
,
…,
![]() ,
не все равные
нулю такие, что
,
не все равные
нулю такие, что
![]() .
.
В противном случае система векторов называется линейно независимой.
Предложение 1.1. Система векторов, содержащая не менее двух векторов, линейно зависима тогда и только тогда, когда какой-нибудь вектор этой системы представим в виде линейной комбинации остальных.
Доказательство.
Пусть система векторов
![]() ,
,![]() ,
…,
,
…,
![]() линейно зависима. В соответствии с
определением существуют числа
линейно зависима. В соответствии с
определением существуют числа
![]() ,
,
![]() ,
…,
,
…,
![]() ,
не все равные нулю такие, что
,
не все равные нулю такие, что
![]() .
.
Пусть, например,
![]() .
Тогда
.
Тогда
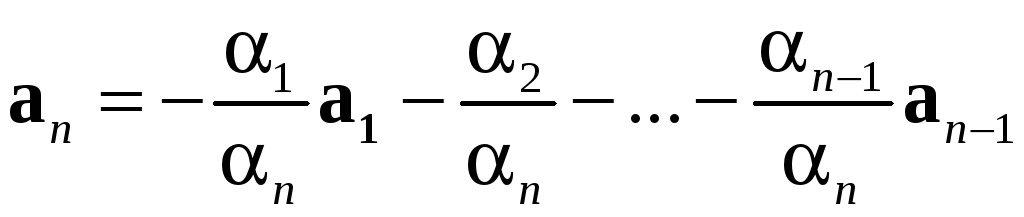 ,
,
т.е. вектор
![]() представлен в виде линейной комбинации
векторов
представлен в виде линейной комбинации
векторов
![]() ,
,![]() ,
…,
,
…,
![]() .
.
Обратно, пусть
какой-нибудь вектор, например
![]() ,
представим в виде линейной комбинации
остальных:
,
представим в виде линейной комбинации
остальных:
![]() .
.
Отсюда
![]() .
.
Так как коэффициент
при
![]() здесь не равен нулю, то векторы линейно
зависимы.
здесь не равен нулю, то векторы линейно
зависимы.
Замечание 1.1. Понятие линейной зависимости является алгебраическим. Геометрические его выражения – коллинеарность в двумерном случае и компланарность – в трехмерном.
Предложение 1.2.
Если при
добавлении вектора
![]() к линейно
независимой системе
к линейно
независимой системе
![]() ,
,![]() ,
…,
,
…,
![]() получаем
линейно зависимую систему, то вектор
получаем
линейно зависимую систему, то вектор
![]() линейно
выражается через векторы
линейно
выражается через векторы
![]() ,
,![]() ,
…,
,
…,
![]() .
.
Доказательство.
Найдутся такие числа
![]() ,
,
![]() ,
…,
,
…,
![]() ,
,![]() ,
не все равные нулю,
что
,
не все равные нулю,
что
![]() .
.
![]()
Тогда именно
![]() .
Действительно, если
.
Действительно, если
![]() ,
то
,
то
![]() и, следовательно, равенство
и, следовательно, равенство
![]() превращается в равенство
превращается в равенство
![]()
и среди чисел
![]() ,
,
![]() ,
…,
,
…,
![]() ,
,![]() найдется отличное от нуля. Тогда система
найдется отличное от нуля. Тогда система
![]() ,
,![]() ,
…,
,
…,
![]() линейно зависима. Противоречие.
линейно зависима. Противоречие.
Следовательно,
![]() и из
и из
![]() получаем
получаем
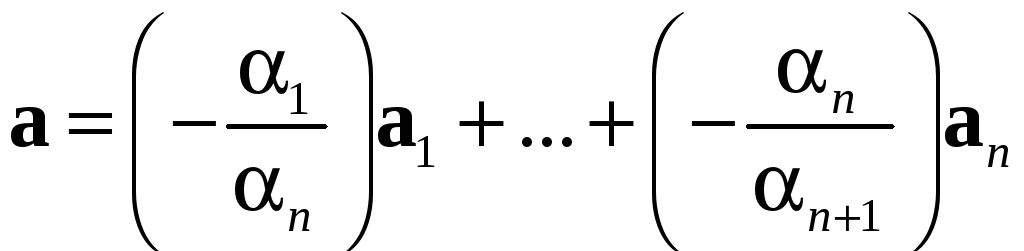 .
.
Предложение доказано.
Матрицы и детерминанты второго и третьего порядков
Для компактности
некоторых записей нам будет удобно
использовать определители второго и
третьего порядков. Введем их определения.
В будущем рассмотрим подробно свойства
определителей
![]() –го
порядка.
–го
порядка.
Матрицей второго порядка называют таблицу чисел
 .
.
Число, равное
![]() ,
называется детерминантом
(или
определителем)
этой матрицы или просто детерминантом
второго порядка. Оно обозначается одним
из символов:
,
называется детерминантом
(или
определителем)
этой матрицы или просто детерминантом
второго порядка. Оно обозначается одним
из символов:
 ,
,
![]() ,
,
![]() .
.
Матрицей третьего порядка называют таблицу чисел
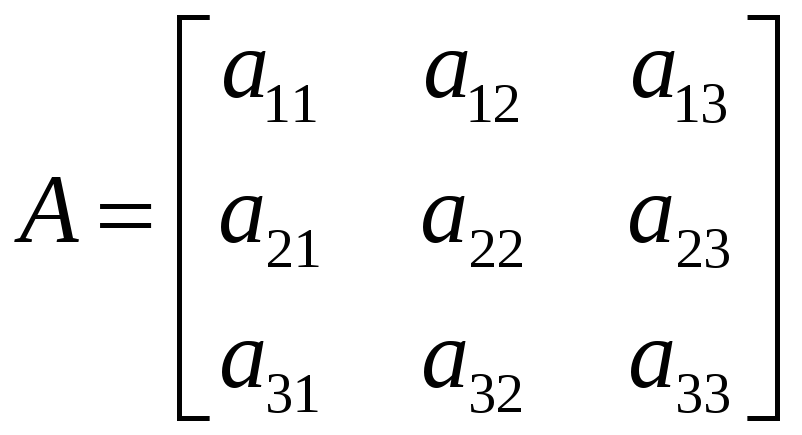 .
.
Числа, составляющие матрицу, называют элементами матрицы. При этом первый индекс элемента матрицы означает номер строки, а второй – номер столбца, на пересечении которых стоит данный элемент. Число
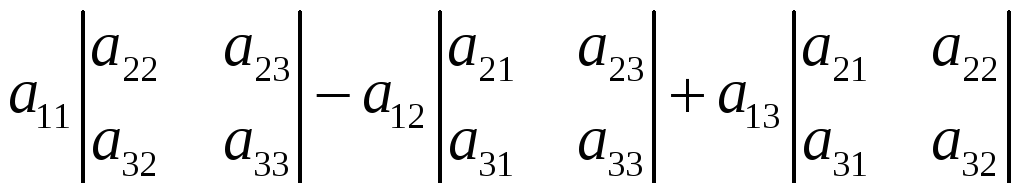
![]()
называется детерминантом этой матрицы (или детерминантом третьего порядка). Оно обозначается одним из символов:
 ,
,
![]() ,
,
![]() .
.
Упражнение
1.1. Доказать:
а) два вектора линейно зависимы тогда и только тогда, когда они коллинеарны;
б) доказать, что три вектора линейно зависимы тогда и только тогда, когда они компланарны;
в) любые четыре вектора линейно зависимы.
1.2.
Докажите, что вектора
![]() ,
,
![]() ,
…,
,
…,
![]() линейно
независимы тогда и только тогда, когда
равенство
линейно
независимы тогда и только тогда, когда
равенство
![]() выполняется
лишь при нулевых коэффициентах
выполняется
лишь при нулевых коэффициентах
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
1.3. Доказать, что радиус-вектор центра правильного многоугольника есть среднее арифметическое радиус-векторов его вершин.
1.4.
В точках пространства, имеющих
радиус-векторы
![]() ,
сосредоточены массы
,
сосредоточены массы
![]() .
Найти радиус-вектор центра тяжести этой
материальной системы.
.
Найти радиус-вектор центра тяжести этой
материальной системы.
1.5. Доказать, что если диагонали четырехугольника в точке пересечения делятся пополам, то этот четырехугольник – параллелограмм.
1.6. Доказать, что средняя линия трапеции параллельна основаниям, а длина средней линии равна полусумме длин оснований (теорема о средней линии трапеции).
1.7. Какому условию должны удовлетворять три вектора, чтобы из них можно было образовать треугольник?
1.8. Можно ли построить треугольник, стороны которого равны и параллельны медианам данного треугольника?
1.9.
Пусть векторы
![]() некомпланарны.
Показать, что четыре точки
некомпланарны.
Показать, что четыре точки
![]() и
и
![]() ,где
,где
![]() ,
лежат в одной
плоскости тогда и только тогда, когда
,
лежат в одной
плоскости тогда и только тогда, когда
![]()
1.10. Даны радиус-векторы вершин треугольника. Доказать, что медианы треугольника пересекаются в одной точке, и найти радиус-вектор этой точки.
1.11. Доказать, что биссектрисы треугольника пересекаются в одной точке.
1.12. Даны радиус-векторы вершин треугольника и длины его сторон. Найти радиус-вектор точки пересечения биссектрис треугольника.
Вопросы для самопроверки
1. Почему повороты не являются векторными величинами?
2. Что такое аксиальный вектор?
3. Сформулируйте различные критерии линейной (не)зависимости.
4. Какова связь коллинеарности и компланарности с линейной зависимостью?
