05. Явления при замыкании тока

Процесс замыкания

Пусть цепь состоит из источника постоянного ЭДС, катушки самоиндукции и омического сопротивления. Полную индуктивность цепи обозначим через , а полное сопротивление – через . При замыкании ключа К ток не сразу достигает предельного значения , определяемого законом Ома, а нарастает постепенно. При этом возрастает также магнитный поток, пронизывающий контур цепи. Возникает электродвижущая сила индукции и соответствующий ей индукционный ток. Этот ток называют экстратоком замыкания. Согласно правилу Ленца направление экстратока замыкания противоположно направлению основного тока.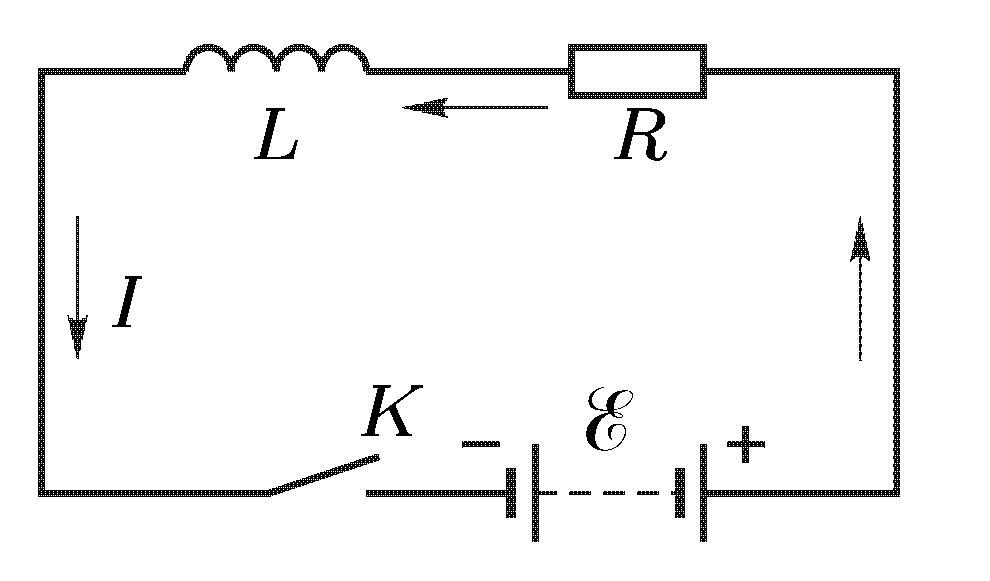

Сила переменного тока не обязательно должна быть одной и той же на всех участках провода, так как в отдельных местах возможно накопление зарядов. Однако мы рассмотрим здесь только такие переменные токи, которые меняются во времени сравнительно медленно. Тогда мгновенные значения токов во всех участках неразветвленной цепи с высокой степенью точности одинаковы, а магнитный поля внутри проводов могут вычисляться по закону Био и Савара, как если бы токи были постоянными. Такие токи называются квазистационарными.

Сила тока определяется выражением

В практических единицах

Дифференциальное уравнение для квазистационарных токов

Если за время изменения тока провода не деформируются, то индуктивность , постоянна и может быть вынесена из-под знака производной

При постоянном значении общее решение этого уравнения имеет вид

Постоянная интегрирования C должна определяться из начального условия: в момент замыкания, т.е. при , то ток равен нулю. Используя это условие, находим . Эта формула применима в любой системе единиц.

Где - постоянная, имеющая размерность времени:

В гауссовской системе единиц:

• - время установления тока

Полный ток I состоит из двух слагаемых, из которых второе, т.е. , определяет силу экстратока замыкания. При экстра ток стремится к нулю, а полный ток I – к своему предельному значению . Таким образом, окончательное значение тока устанавливается постепенно. Быстроту установления определяется временем : по истечении времени сила экстратока убывает в раз.

06. Явления при размыкании тока

Ключ К сначала замкнут. Направление токов показаны сплошными стрелками. Общий ток распределяется между параллельно включенными самоиндукцией и омическим сопротивлением . Если внутреннее сопротивление батареи пренебрежимо мало, то ток в катушке самоиндукции будет равен . После размыкания ключа К замкнутым останется только контур ABCD. Первоначальный ток, существовавший в катушке самоиндукции, обладал определенным запасом магнитной энергии, которая исчезает не сразу. Магнитное поле начнет убывать. Это возбудит электродвижущую силу и индукционный ток в контуре ABCD. Такой ток называется экстратоком размыкания. Экстраток показан пунктирными стрелками. В катушке самоиндукции экстраток течет в том же направлении , что и первоначальный ток, в остальных участках контура ABCD — в противоположном направлении. Если - общее сопротивление контура ABCD, то сила тока определится из дифференциального уравнения

и начального условия: . Это дает , где определяется прежним выражением. Электродвижущая сила индукции равна

Если , то эта величина может значительно превзойти ЭДС батареи. В этом причина электрического пробоя, наблюдающегося иногда при выключении тока в цепях, содержащих большие индуктивности.

Для демонстрации явления можно взять катушку длиной 50-60 см и диаметром 8-10 см сердечником из железных прутьев и обмоткой из нескольких слоев проволоки диаметром около 1 мм. Параллельно катушке присоединена лампочка. Лампочка рассчитана на напряжение, несколько превышающее ЭДС батареи. При замкнутой цепи лампочка горит тускло. При размыкании ключа К она ярко вспыхивает и даже может перегореть, так как ЭДС индукции превосходит в несколько раз ЭДС батареи.

Рассмотрим теперь два витка (или две катушки), по которым текут постоянные токи и . Установим произвольно на этих витках положительные направления обхода. Если в окружающем пространстве нет ферромагнетиков, то магнитные потоки через витки и пропорциональны токам и могут быть представлены в виде

Коэффициенты не зависят от токов, а определяются лишь формой, размерами и взаимным расположением витков. Они называются коэффициентами индуктивности. Если . Поэтому есть индуктивность первого, а - второго витка. Оставшиеся два коэффициента и называются взаимными индуктивностями или коэффициентами взаимной индукции.