
- •О.И.Москвич общая физика Молекулярная физика
- •Предисловие
- •I. Основы молекулярной статистики
- •1.1. Предмет молекулярной физики
- •1.2. Масштабы физических величин в молекулярном мире
- •1.3. Теоретические и экспериментальные методы молекулярной физики
- •1.4. Эволюция молекулярных систем. Порядок и хаос
- •1.5. Принципы организации статистического и термодинамического методов изучения макросистем
- •Статистический метод
- •Термодинамический метод
- •2.1. Классификация моделей молекулярных систем
- •2.2. Идеальные статистические системы
- •Модели идеальных систем
- •2.3. Элементарные сведения из теории вероятностей
- •Случайные события
- •Определения вероятности событий
- •Статистическое или частотное определение вероятности.
- •Теоремы теории вероятностей
- •Условие нормировки вероятности
- •Случайная величина
- •Плотность вероятности
- •2.4. Основные понятия молекулярной статистики
- •Вероятность микроскопического состояния. Статистический ансамбль
- •Статистические постулаты
- •Комментарий к постулату равновероятности
- •Эргодическая гипотеза:
- •Постулат равновероятности доступных микроскопических состояний изолированной системы в состоянии термодинамического
- •Комментарий к эргодической гипотезе
- •Вероятность макроскопического состояния
- •3.1. Вывод закона распределения вероятностей Описание системы
- •Актуальные свойства модели системы
- •Постановка задачи
- •Вывод закона
- •Математические преобразования больших чисел. Введение общепринятых обозначений
- •Формула для вероятности макросостояния. Закон Бернулли, или биномиальное распределение.
- •3.2. Графическое представление биномиального распределения.
- •Основные характеристики биномиального распределении.
- •3.3. Предельные случаи биномиального распределения
- •4.1. Распределение энергии в статической системе
- •Вывод распределения Гиббса
- •4.2. Вывод распределения Максвелла
- •4.3. Плотность вероятности и характерные скорости распределения Максвелла
- •4.4. Распределение Максвелла по компонентам скорости
- •4.5. Экспериментальная проверка распределения Максвелла
- •5.1. Вывод формулы для давления идеального газа
- •5.2. Основное уравнение молекулярно-кинетической теории. Газовые законы
- •5.3. Уравнение эффузии
- •5.4. Измерение давления
- •5.5. Определение и измерение температуры
- •5.6. Построение эмпирической шкалы на основе газового термометра
- •Преимущества газовой шкалы температур
- •Построение газовой шкалы температур
- •Термодинамическая шкала температур
- •6.1. Распределение молекул по энергиям во внешнем потенциальном поле
- •6.2. Формула Больцмана для концентрации молекул в потенциальном поле
- •6.3. Зависимость концентрации молекул газа от координат в однородном гравитационном поле и поле центробежных сил
- •Графическое представление зависимости концентрации молекул от координат
- •6.4. Экспериментальное подтверждение распределения Больцмана: опыты Перрена
- •Получение макромолекул
- •Выделение частиц одинакового размера
- •Измерение диаметра макромолекулы
- •Подсчёт количества частиц на определённой высоте
- •6.5. Барометрическая формула
- •6.6. Закон распределения Максвелла – Больцмана
- •7.1. Формулировка теоремы и её доказательство Формулировка теоремы
- •Актуальные свойства модели статистической системы
- •Доказательство теоремы
- •7.2. Статистические степени свободы
- •7.3. Броуновское движение и его статистическое описание
- •Поступательное броуновское движение
- •Вращательное броуновское движение
- •7.4. Броуновский критерий точности физических измерений
- •7.5. Классическая теория теплоёмкости многоатомных газов. Область её применимости
- •7.6. Классическая теория теплоёмкости твёрдых тел.
- •7.7. Применение квантовых моделей в теории теплоёмкости твёрдых тел
- •Модель Эйнштейна
- •Модель Дебая
- •II. Основы термодинамики
- •8.1. Четыре постулата термодинамики
- •8.2. Нулевое (общее) начало термодинамики
- •Формулировка постулата
- •Свойство транзитивности термодинамического равновесия
- •Информационное содержание постулата
- •Фундаментальное и прикладное значение постулата
- •8.3. Макроскопические процессы
- •8.4. Функция состояния
- •Математические свойства функции состояния
- •8.5. Внутренняя энергия системы. Работа и теплота Внутренняя энергия
- •Макроскопическая работа и теплота
- •8.6. Калорическое и термическое уравнения состояния
- •9.1. Первое начало термодинамики
- •Формулировка постулата
- •Математическая запись постулата
- •Информационное содержание постулата
- •Фундаментальное и прикладное значение постулата
- •9.2. Теплоёмкость
- •Связь между теплоёмкостями и(общий случай)
- •Уравнение Роберта Майера
- •9.3. Политропические процессы в идеальном газе
- •Вывод уравнения политропического процесса в идеальном газе
- •9.4. Тепловые машины и их эффективность.
- •Принципиальная схема работы тепловой машины
- •Показатели эффективности тепловых машин
- •10.1. Цикл Карно
- •Расчёт кпд машины Карно
- •10.2. Теоремы Карно
- •Термодинамическая шкала температур
- •10.3. Метод циклов
- •Задача о нахождении зависимости внутренней энергии макроскопического тела от его объема
- •10.4. Неравенство Клаузиуса. Определение энтропии
- •10.5. Оценка эффективности тепловых машин сверху
- •Примеры оценок эффективности тепловых машин сверху кпд бензинового двигателя внутреннего сгорания
- •Кпд паровой турбины
- •Киэ бытового холодильника
- •Киэ кондиционера воздуха
- •Киэ теплового насоса
- •Тепловое загрязнение окружающей среды
- •11.1. Формулировки второго начала термодинамики
- •Энтропийная формулировка второго начала термодинамики Часть первая
- •Часть вторая
- •Информационное содержание постулата
- •11.2. Закон возрастания энтропии в изолированных системах
- •Демон Максвелла
- •Формулировка парадокса
- •Разрешение парадокса
- •11.3. Область применимости второго начала термодинамики
- •Статистический характер второго начала
- •11.4. Концепция тепловой смерти Вселенной
- •Концепция Клаузиуса
- •Флуктуационная гипотеза Больцмана
- •Несостоятельность концепции тепловой смерти Вселенной
- •11.5. Энтропия и её изменение в различных процессах
- •Постановка задачи
- •Описание системы
- •Актуальные свойства системы и процесса
- •Решение
- •Парадокс Гиббса Описание
- •По разные стороны перегородки находятся различные газы. После устранения перегородки начнется диффузия.
- •По разные стороны перегородки находится один и тот же газ.
- •12.1. Термодинамические функции
- •Свободная энергия
- •Термодинамический потенциал Гиббса
- •12.3. Условия термодинамической устойчивости макроскопических систем. Принцип Ле Шателье-Брауна
- •Принцип Ле Шателье-Брауна
- •Проведение полного термодинамического анализа вещества на полуэмпирической основе
- •12.4. Третье начало термодинамики
- •Формулировка постулата
- •Математическая запись постулата (варианты)
- •Информационное содержание постулата
- •Статус постулата
- •Следствия третьего начала
- •III. Физика реальных макросистем
- •13.1. Твердые тела
- •13.2. Реальные газы и жидкости
- •Потенциал межмолекулярного взаимодействия
- •Природа межмолекулярного взаимодействия
- •Структура жидкостей
- •13.3. Переход из газообразного состояния в жидкое.
- •13.4. Уравнения состояния реального газа
- •13.5. Модель газа Ван-дер-Ваальса. Уравнение Ван-дер-Ваальса
- •14.1. Изотермы газа Ван-дер-Ваальса
- •14.2. Критическое состояние вещества
- •Закон соответственных состояний
- •Свойства вещества в критическом состоянии
- •Анализ применения уравнения Ван-дер-Ваальса для описания свойств реальных газов
- •14.3. Внутренняя энергия газа Ван-дер-Ваальса
- •14.4. Эффект Джоуля-Томсона Основные определения
- •Описание процесса Джоуля-Томсона
- •Сущность эффекта Джоуля-Томсона
- •Расчет дифференциального эффекта Джоуля-Томсона
- •Расчет интегрального эффекта Джоуля-Томсона
- •14.5. Методы получения низких температур
- •Метод противоточного обмена теплотой
- •Метод адиабатического размагничивания
- •15.1. Условие равновесия фаз химически однородного вещества
- •15.2. Классификация фазовых переходов по Эренфесту
- •Фазовые переходы первого рода
- •Фазовые переходы второго рода
- •15.3. Фазовые переходы первого рода. Диаграмма состояний
- •15.4. Уравнение Клапейрона-Клаузиуса
- •Вывод уравнения Клапейрона-Клаузиуса
- •Вывод уравнения Клапейрона-Клаузиуса методом циклов
- •Актуальные свойства процесса
- •Постановка задачи
- •Вывод уравнения
- •15.5. Диаграмма состояний гелия. Сверхтекучесть жидкого гелия.
- •16.1. Релаксационные процессы в молекулярных системах
- •16.2. Стационарные уравнения переноса в газах, жидкостях и твердых телах
- •Уравнение теплопроводности
- •Уравнение самодиффузии
- •Уравнение внутреннего трения
- •16.3. Внутренняя теплопроводность и внешняя теплопередача
- •Стационарное распределение температуры в бесконечной плоско-параллельной пластинке
- •Стационарное распределение температуры между двумя концентрическими бесконечно длинными цилиндрами
- •Стационарное распределение температуры между двумя концентрическими сферами
- •Внешняя теплопередача
- •17.1. Столкновения молекул и их количественные характеристики
- •Эффективное сечение молекул
- •Средняя длина свободного пробега молекулы
- •Кинематические параметры и
- •17.2. Обобщенное уравнение переноса
- •Вывод обобщенного уравнения процесса Описание системы
- •Актуальные свойства модели процесса
- •Постановка задачи
- •Вывод уравнения
- •17.3. Элементарная кинетическая теория теплопроводности,
- •17.4. Явления переноса в ультраразреженных газах
- •Трение и теплопроводность ультраразреженных газов
- •Тепловая и изотермическая эффузия
- •18.1. Атмосфера как открытая система и как открытая книга
- •18.2. Состав и структура атмосферы Земли.
- •18.3. Термофизическая модель атмосферы
- •18.4. Парниковый эффект
- •Сущность парникового эффекта
- •Парниковые газы
- •Проблема глобального потепления
- •Киотский протокол
- •18.5. Инверсия температуры в стратосфере. Озоносфера Земли
- •Мониторинг озонового слоя
- •Монреальский Протокол
- •18.6. Концепция «ядерной зимы»
- •«Ядерная зима» Сценарии ядерной войны
- •Огненные смерчи – суперподъемники
- •Антипарниковый эффект
- •Глобальный характер климатических последствий
- •Список литературы
- •Общая физика. Молекулярная физика
- •660041, Г. Красноярск, пр. Свободный, 79
16.1. Релаксационные процессы в молекулярных системах
В равновесных системах, изучением которых мы занимались до настоящего времени, температура и другие макроскопические параметры были постоянными во всех частях системы. Если это условие нарушено, то система является неравновесной. Наличие градиентов температуры, концентрации частиц, электрического потенциалов приводит к возникновению потоков энергии, вещества или заряда. Подобные процессы являются необратимыми и называются процессами переноса.
Изолированная система, предоставленная
самой себе, будет постепенно переходить
к равновесному состоянию. Как вы помните,
время, в течение которого система
достигает равновесного состояния,
называется временем релаксации и обычно
обозначается буквой
 .
Если отклонение от равновесия происходит
по нескольким параметрам, то времена
релаксации
.
Если отклонение от равновесия происходит
по нескольким параметрам, то времена
релаксации по этим параметрам различаются
между собой. Распределение Максвелла
по скоростям мы вывели и применяли для
идеального газа, однако оно также
справедливо для реальных газов и
жидкостей, лишь бы система находилась
в термодинамическом равновесии. Время,
в течение которого система приходит к
распределению Максвелла, называется
временем релаксации к распределению
Максвелла или временем термализации
по этим параметрам различаются
между собой. Распределение Максвелла
по скоростям мы вывели и применяли для
идеального газа, однако оно также
справедливо для реальных газов и
жидкостей, лишь бы система находилась
в термодинамическом равновесии. Время,
в течение которого система приходит к
распределению Максвелла, называется
временем релаксации к распределению
Максвелла или временем термализации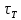 .
.
Неравновесная смесь нескольких газов
придет к распределению Максвелла с
разными для каждой компоненты
 временами термализации
временами термализации .
В отсутствие внешних силовых полей, как
мы знаем, концентрация частиц постоянна
по всему объему, занимаемому системой.
Выведенная из равновесия по этому
параметру макросистема спустя время
релаксации
.
В отсутствие внешних силовых полей, как
мы знаем, концентрация частиц постоянна
по всему объему, занимаемому системой.
Выведенная из равновесия по этому
параметру макросистема спустя время
релаксации вернется к однородному распределению
молекул. Однако это время релаксации
не равно времени термализации той же
системы. Время релаксации для концентрации
частиц во внешнем силовом поле, например,
в поле тяжести, отличается от времени
релаксации для концентрации в отсутствии
консервативных сил. Оценка различных
времен релаксации имеет большое значение.
Процессы с самыми короткими временами
релаксации приводят систему очень
быстро к состоянию равновесия по этим
параметрам и анализ приближения системы
к равновесию по оставшимся параметрам
существенно упрощается.
вернется к однородному распределению
молекул. Однако это время релаксации
не равно времени термализации той же
системы. Время релаксации для концентрации
частиц во внешнем силовом поле, например,
в поле тяжести, отличается от времени
релаксации для концентрации в отсутствии
консервативных сил. Оценка различных
времен релаксации имеет большое значение.
Процессы с самыми короткими временами
релаксации приводят систему очень
быстро к состоянию равновесия по этим
параметрам и анализ приближения системы
к равновесию по оставшимся параметрам
существенно упрощается.
Сравнение времен релаксации предполагает, что размер системы фиксирован, имеется в виду её масса, объем, количество частиц. Время релаксации растет с увеличением размеров системы. Самопроизвольный переход отдельных макроскопических малых частей системы в равновесное состояние осуществляется значительно раньше, чем устанавливается равновесие между этими частями.
В термодинамике неравновесных систем
исходят из представления о локальном
равновесии. Суть его в том, что хотя в
целом состояние системы является
неравновесным, отдельные её малые части
равновесны (квазиравновесны) в том
смысле, что термодинамические параметры
в этих физически малых частях медленно
изменяются во времени и от точки к точке.
Размеры этих равновесных областей в
неравновесной системе выбираются таким
образом, чтобы время
 изменения термодинамических параметров
было намного больше времени
изменения термодинамических параметров
было намного больше времени релаксации в них и намного меньше времени
релаксации всей системы
релаксации в них и намного меньше времени
релаксации всей системы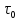

Исходное положение о локальном равновесии позволяет построить последовательную феноменологическую термодинамику необратимых процессов, рассмотрение которой выходит за рамки этого курса.
Строгая молекулярно-кинетическая теория
явлений переноса очень сложна. Она
сводится к приближенным решениям, так
называемого, кинетического уравнения
Больцмана. Уравнение Больцмана – это
нестационарное интегро-дифференциальное
уравнение для функции распределения
 в неравновесном состоянии. Рассмотрением
этого уравнения вы займетесь в курсе
«Статистическая физика», после того,
как существенно усилите свою математическую
подготовку. Мы же ограничимся элементарной
теорией явлений переноса, а именно,
методом средней длины свободного
пробега. Прежде чем обратиться к
микроскопической теории, проанализируем
процессы переноса в рамках феноменологического
похода.
в неравновесном состоянии. Рассмотрением
этого уравнения вы займетесь в курсе
«Статистическая физика», после того,
как существенно усилите свою математическую
подготовку. Мы же ограничимся элементарной
теорией явлений переноса, а именно,
методом средней длины свободного
пробега. Прежде чем обратиться к
микроскопической теории, проанализируем
процессы переноса в рамках феноменологического
похода.
