
- •О.И.Москвич общая физика Молекулярная физика
- •Предисловие
- •I. Основы молекулярной статистики
- •1.1. Предмет молекулярной физики
- •1.2. Масштабы физических величин в молекулярном мире
- •1.3. Теоретические и экспериментальные методы молекулярной физики
- •1.4. Эволюция молекулярных систем. Порядок и хаос
- •1.5. Принципы организации статистического и термодинамического методов изучения макросистем
- •Статистический метод
- •Термодинамический метод
- •2.1. Классификация моделей молекулярных систем
- •2.2. Идеальные статистические системы
- •Модели идеальных систем
- •2.3. Элементарные сведения из теории вероятностей
- •Случайные события
- •Определения вероятности событий
- •Статистическое или частотное определение вероятности.
- •Теоремы теории вероятностей
- •Условие нормировки вероятности
- •Случайная величина
- •Плотность вероятности
- •2.4. Основные понятия молекулярной статистики
- •Вероятность микроскопического состояния. Статистический ансамбль
- •Статистические постулаты
- •Комментарий к постулату равновероятности
- •Эргодическая гипотеза:
- •Постулат равновероятности доступных микроскопических состояний изолированной системы в состоянии термодинамического
- •Комментарий к эргодической гипотезе
- •Вероятность макроскопического состояния
- •3.1. Вывод закона распределения вероятностей Описание системы
- •Актуальные свойства модели системы
- •Постановка задачи
- •Вывод закона
- •Математические преобразования больших чисел. Введение общепринятых обозначений
- •Формула для вероятности макросостояния. Закон Бернулли, или биномиальное распределение.
- •3.2. Графическое представление биномиального распределения.
- •Основные характеристики биномиального распределении.
- •3.3. Предельные случаи биномиального распределения
- •4.1. Распределение энергии в статической системе
- •Вывод распределения Гиббса
- •4.2. Вывод распределения Максвелла
- •4.3. Плотность вероятности и характерные скорости распределения Максвелла
- •4.4. Распределение Максвелла по компонентам скорости
- •4.5. Экспериментальная проверка распределения Максвелла
- •5.1. Вывод формулы для давления идеального газа
- •5.2. Основное уравнение молекулярно-кинетической теории. Газовые законы
- •5.3. Уравнение эффузии
- •5.4. Измерение давления
- •5.5. Определение и измерение температуры
- •5.6. Построение эмпирической шкалы на основе газового термометра
- •Преимущества газовой шкалы температур
- •Построение газовой шкалы температур
- •Термодинамическая шкала температур
- •6.1. Распределение молекул по энергиям во внешнем потенциальном поле
- •6.2. Формула Больцмана для концентрации молекул в потенциальном поле
- •6.3. Зависимость концентрации молекул газа от координат в однородном гравитационном поле и поле центробежных сил
- •Графическое представление зависимости концентрации молекул от координат
- •6.4. Экспериментальное подтверждение распределения Больцмана: опыты Перрена
- •Получение макромолекул
- •Выделение частиц одинакового размера
- •Измерение диаметра макромолекулы
- •Подсчёт количества частиц на определённой высоте
- •6.5. Барометрическая формула
- •6.6. Закон распределения Максвелла – Больцмана
- •7.1. Формулировка теоремы и её доказательство Формулировка теоремы
- •Актуальные свойства модели статистической системы
- •Доказательство теоремы
- •7.2. Статистические степени свободы
- •7.3. Броуновское движение и его статистическое описание
- •Поступательное броуновское движение
- •Вращательное броуновское движение
- •7.4. Броуновский критерий точности физических измерений
- •7.5. Классическая теория теплоёмкости многоатомных газов. Область её применимости
- •7.6. Классическая теория теплоёмкости твёрдых тел.
- •7.7. Применение квантовых моделей в теории теплоёмкости твёрдых тел
- •Модель Эйнштейна
- •Модель Дебая
- •II. Основы термодинамики
- •8.1. Четыре постулата термодинамики
- •8.2. Нулевое (общее) начало термодинамики
- •Формулировка постулата
- •Свойство транзитивности термодинамического равновесия
- •Информационное содержание постулата
- •Фундаментальное и прикладное значение постулата
- •8.3. Макроскопические процессы
- •8.4. Функция состояния
- •Математические свойства функции состояния
- •8.5. Внутренняя энергия системы. Работа и теплота Внутренняя энергия
- •Макроскопическая работа и теплота
- •8.6. Калорическое и термическое уравнения состояния
- •9.1. Первое начало термодинамики
- •Формулировка постулата
- •Математическая запись постулата
- •Информационное содержание постулата
- •Фундаментальное и прикладное значение постулата
- •9.2. Теплоёмкость
- •Связь между теплоёмкостями и(общий случай)
- •Уравнение Роберта Майера
- •9.3. Политропические процессы в идеальном газе
- •Вывод уравнения политропического процесса в идеальном газе
- •9.4. Тепловые машины и их эффективность.
- •Принципиальная схема работы тепловой машины
- •Показатели эффективности тепловых машин
- •10.1. Цикл Карно
- •Расчёт кпд машины Карно
- •10.2. Теоремы Карно
- •Термодинамическая шкала температур
- •10.3. Метод циклов
- •Задача о нахождении зависимости внутренней энергии макроскопического тела от его объема
- •10.4. Неравенство Клаузиуса. Определение энтропии
- •10.5. Оценка эффективности тепловых машин сверху
- •Примеры оценок эффективности тепловых машин сверху кпд бензинового двигателя внутреннего сгорания
- •Кпд паровой турбины
- •Киэ бытового холодильника
- •Киэ кондиционера воздуха
- •Киэ теплового насоса
- •Тепловое загрязнение окружающей среды
- •11.1. Формулировки второго начала термодинамики
- •Энтропийная формулировка второго начала термодинамики Часть первая
- •Часть вторая
- •Информационное содержание постулата
- •11.2. Закон возрастания энтропии в изолированных системах
- •Демон Максвелла
- •Формулировка парадокса
- •Разрешение парадокса
- •11.3. Область применимости второго начала термодинамики
- •Статистический характер второго начала
- •11.4. Концепция тепловой смерти Вселенной
- •Концепция Клаузиуса
- •Флуктуационная гипотеза Больцмана
- •Несостоятельность концепции тепловой смерти Вселенной
- •11.5. Энтропия и её изменение в различных процессах
- •Постановка задачи
- •Описание системы
- •Актуальные свойства системы и процесса
- •Решение
- •Парадокс Гиббса Описание
- •По разные стороны перегородки находятся различные газы. После устранения перегородки начнется диффузия.
- •По разные стороны перегородки находится один и тот же газ.
- •12.1. Термодинамические функции
- •Свободная энергия
- •Термодинамический потенциал Гиббса
- •12.3. Условия термодинамической устойчивости макроскопических систем. Принцип Ле Шателье-Брауна
- •Принцип Ле Шателье-Брауна
- •Проведение полного термодинамического анализа вещества на полуэмпирической основе
- •12.4. Третье начало термодинамики
- •Формулировка постулата
- •Математическая запись постулата (варианты)
- •Информационное содержание постулата
- •Статус постулата
- •Следствия третьего начала
- •III. Физика реальных макросистем
- •13.1. Твердые тела
- •13.2. Реальные газы и жидкости
- •Потенциал межмолекулярного взаимодействия
- •Природа межмолекулярного взаимодействия
- •Структура жидкостей
- •13.3. Переход из газообразного состояния в жидкое.
- •13.4. Уравнения состояния реального газа
- •13.5. Модель газа Ван-дер-Ваальса. Уравнение Ван-дер-Ваальса
- •14.1. Изотермы газа Ван-дер-Ваальса
- •14.2. Критическое состояние вещества
- •Закон соответственных состояний
- •Свойства вещества в критическом состоянии
- •Анализ применения уравнения Ван-дер-Ваальса для описания свойств реальных газов
- •14.3. Внутренняя энергия газа Ван-дер-Ваальса
- •14.4. Эффект Джоуля-Томсона Основные определения
- •Описание процесса Джоуля-Томсона
- •Сущность эффекта Джоуля-Томсона
- •Расчет дифференциального эффекта Джоуля-Томсона
- •Расчет интегрального эффекта Джоуля-Томсона
- •14.5. Методы получения низких температур
- •Метод противоточного обмена теплотой
- •Метод адиабатического размагничивания
- •15.1. Условие равновесия фаз химически однородного вещества
- •15.2. Классификация фазовых переходов по Эренфесту
- •Фазовые переходы первого рода
- •Фазовые переходы второго рода
- •15.3. Фазовые переходы первого рода. Диаграмма состояний
- •15.4. Уравнение Клапейрона-Клаузиуса
- •Вывод уравнения Клапейрона-Клаузиуса
- •Вывод уравнения Клапейрона-Клаузиуса методом циклов
- •Актуальные свойства процесса
- •Постановка задачи
- •Вывод уравнения
- •15.5. Диаграмма состояний гелия. Сверхтекучесть жидкого гелия.
- •16.1. Релаксационные процессы в молекулярных системах
- •16.2. Стационарные уравнения переноса в газах, жидкостях и твердых телах
- •Уравнение теплопроводности
- •Уравнение самодиффузии
- •Уравнение внутреннего трения
- •16.3. Внутренняя теплопроводность и внешняя теплопередача
- •Стационарное распределение температуры в бесконечной плоско-параллельной пластинке
- •Стационарное распределение температуры между двумя концентрическими бесконечно длинными цилиндрами
- •Стационарное распределение температуры между двумя концентрическими сферами
- •Внешняя теплопередача
- •17.1. Столкновения молекул и их количественные характеристики
- •Эффективное сечение молекул
- •Средняя длина свободного пробега молекулы
- •Кинематические параметры и
- •17.2. Обобщенное уравнение переноса
- •Вывод обобщенного уравнения процесса Описание системы
- •Актуальные свойства модели процесса
- •Постановка задачи
- •Вывод уравнения
- •17.3. Элементарная кинетическая теория теплопроводности,
- •17.4. Явления переноса в ультраразреженных газах
- •Трение и теплопроводность ультраразреженных газов
- •Тепловая и изотермическая эффузия
- •18.1. Атмосфера как открытая система и как открытая книга
- •18.2. Состав и структура атмосферы Земли.
- •18.3. Термофизическая модель атмосферы
- •18.4. Парниковый эффект
- •Сущность парникового эффекта
- •Парниковые газы
- •Проблема глобального потепления
- •Киотский протокол
- •18.5. Инверсия температуры в стратосфере. Озоносфера Земли
- •Мониторинг озонового слоя
- •Монреальский Протокол
- •18.6. Концепция «ядерной зимы»
- •«Ядерная зима» Сценарии ядерной войны
- •Огненные смерчи – суперподъемники
- •Антипарниковый эффект
- •Глобальный характер климатических последствий
- •Список литературы
- •Общая физика. Молекулярная физика
- •660041, Г. Красноярск, пр. Свободный, 79
Постановка задачи
Рассчитать изменение энтропии в процессе расширения идеального газа в вакуум в условиях адиабатической оболочки.
Описание системы
В сосуде объёмом
 при температуре
при температуре находится идеальный газ в количестве
находится идеальный газ в количестве молей (рис. 11.5). Если убрать перегородку,
отделяющую объём
молей (рис. 11.5). Если убрать перегородку,
отделяющую объём от объёма
от объёма ,
то начнется процесс расширения газа в
вакуум.
,
то начнется процесс расширения газа в
вакуум.
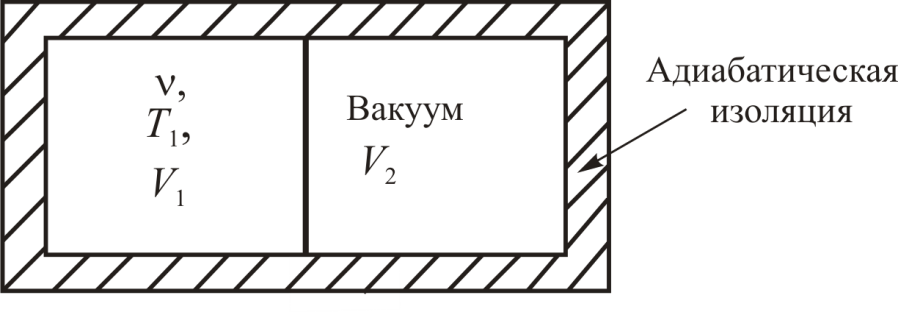
Рис. 11.5.
Актуальные свойства системы и процесса
• Процесс расширения газа в вакуум является необратимым. При быстром расширении давление газа зависит от координат и от времени.
• Газ расширяется в вакуум без совершения
работы. Внешних сил нет, поэтому
 и, следовательно,
и, следовательно, .
.
• Для идеального газа справедливо
уравнение Клапейрона-Менделеева
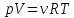 .
.
Решение
Мысленно заменим неравновесный процесс на квазистатический изотермический процесс (рис. 11.6).

Рис. 11.6.
Обратите внимание на то, что в реальном процессе газ работу не совершает, а в фиктивном (воображаемом) процессе газ совершает изотермическую работу против внешних сил за счёт подводимого количества теплоты (изоляции нет!). Газ двигает поршень. Важно, что начальное и конечное состояния в том и другом процессе одинаковы и равновесны.
Для нахождения изменения энтропии
воспользуемся формулой (11.8), тогда при
условии, что
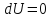 ,
она примет вид
,
она примет вид


Ответ:

Как видно энтропия в процессе расширения идеального газа в вакуум в условиях тепловой изоляции возрастает. Полученная формула (11.11) может быть использована для вычисления изменения энтропии при диффузии идеальных газов и понимания замечательного факта, именуемого парадоксом Гиббса.
Парадокс Гиббса Описание
Изолированная система представляет собой сосуд, разделенный перегородкой на две половины, в каждой из которых находится идеальный газ.
По разные стороны перегородки находятся различные газы. После устранения перегородки начнется диффузия.
По второму началу термодинамики, при взаимной диффузии двух газов энтропия системы увеличивается. Это увеличение нетрудно подсчитать.
Процесс диффузии идеального газа
является необратимым. Мысленно заменим
реальный процесс перемешивания газов
квазистатическим изотермическим
процессом. Действительно, если
первоначально два газа были разделены
перегородкой, находились при одинаковых
давлениях и температурах и занимали
равные объемы
 ,
то после устранения перегородки и
завершения процесса диффузии они займут
объем
,
то после устранения перегородки и
завершения процесса диффузии они займут
объем ,причем температура и давление в смеси
останутся прежними. Найдём изменение
энтропии всей изолированной системы в
целом, если газы по разные стороны
перегородки различные
,причем температура и давление в смеси
останутся прежними. Найдём изменение
энтропии всей изолированной системы в
целом, если газы по разные стороны
перегородки различные

Согласно (11.11)
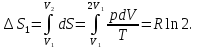
Поэтому

По разные стороны перегородки находится один и тот же газ.
После устранения перегородки начнется самодиффузия
Теперь предположим, что по разные стороны перегородки находится один и тот же газ. После устранения перегородки начнется самодиффузия. С одной стороны, ясно, что устранение перегородки ничего не изменяет в состоянии газа, две части которого объединяются в одну систему. Поэтому в результате устранения перегородки энтропия системы не меняется.
 .
.
Формулировка парадокса
Возрастание энтропии, вызванное смешением разного рода газов при постоянных температурах и давлениях, не зависитoт природы этих газов (пока они разные, подчеркивал Гиббс!), в то время как смешение двух масс одного и того же газа не вызывает возрастания энтропии. Таким образом, при переходе от смеси сколь угодно близких по своим свойствам газов к смеси одинаковых газов изменение энтропии испытывает скачок

В этом скачке энтропии смешения и состоит парадокс Гиббса.
Разрешение парадокса
Парадокс находит своё разрешение в квантовой физике. Число различных типов атомов конечно, поэтому нельзя выполнить предельный переход, в котором бы свойства одного атома переходили в свойства другого.
11.6. Изменение энтропии в процессах самоорганизации открытых систем
В первой лекции нашего курса мы анонсировали «загадку» самоорганизации в открытых системах, находящихся вдали от термодинамического равновесия. Отметим, что возникновение упорядоченной структуры однозначно приводит к уменьшению энтропии в той локальной области пространства, где она формируется. Однако, этот процесс «обязан» сопровождаться компенсацией – возрастанием энтропии в окружающей среде

Если суммарное изменение энтропии оказывается меньше нуля, то процесс самоорганизации не идёт, или если шёл, то прекратится. По этому принципу идут или не идут химические реакции, возникают звёзды, галактики и их скопления, образуются белковые молекулы, живые организмы и вообще все уровни организации живых систем, включая биосферу. Заведите маленького котёнка и вы увидите, что неравенство (11.12) выполняется.
Закон возрастания энтропии в открытой системе нашел свое отражение в трех биогеохимических принципах В.И. Вернадского, основоположника учения о биосфере. Кратко эти принципы можно сформулировать так:
• Биогенная миграция химических элементов в биосфере всегда стремится к максимальному значению.
• Эволюция видов, приводящая к формам жизни, устойчивым в биосфере, идёт в направлении, увеличивающем биогенную миграцию химических элементов.
• В течение всего геологического времени заселение планеты живыми организмами должно быть максимально возможным.
Проанализируйте принципы Вернадского и убедитесь, что они «вырастают» из неравенства (11.12).
Контрольные вопросы
1. Что называется вечным двигателем второго рода?
2. Какие процессы запрещает второе начало термодинамики?
3. Можно ли работу полностью превратить в теплоту (без компенсации)? Приведите пример.
4. Передайте содержание первой части энтропийной формулировки второго начала.
5. Передайте содержание второй части энтропийной формулировки второго начала.
6. Что означает рост энтропии в изолированной системе?
7. Выведите закон возрастания энтропии.
8. В чем заключается парадокс «демона Максвелла» и как он разрешается?
9. Как проявляется статистический характер второго начала термодинамики?
10. Каким образом следует вычислять изменение энтропии для необратимых процессов? Поясните на примере процесса Гей-Люссака.
11. В чем заключается парадокс Гиббса?
12. Как изменяется энтропия в процессах самоорганизации открытых систем? Проанализируйте принципы Вернадского а рамках энтропийного подхода.
ЛЕКЦИЯ 12
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ И УСЛОВИЯ РАВНОВЕСИЯ
Предыдущая лекция была посвящена
изучению различных процессов в
макросистемах с помощью такой функции
состояния как энтропия. Наряду с энтропией
для этих целей можно использовать и
другие, связанные с ней функции состояния.
Функции состояния называются также
термодинамическими функциями или
термодинамическими потенциалами.
Термодинамических функций можно
произвести бесконечное множество. Если
известна одна из них, то любая функция
от этой функции также является
термодинамической функцией, разумеется,
при выполнении условий (8.2) и (8.3). В научной
практике из этого многообразия функций
получили распространение только четыре.
Прежде чем назвать их, запишем равенство,
именуемое основным термодинамическим
тождествомдля обратимых процессов.
Оно объединяет первое начало термодинамики
и определение энтропии для обратимых
процессов. Из (11.1) следует, что и уравнение первого начала обретает
новую содержательную форму
и уравнение первого начала обретает
новую содержательную форму

Во всех обратимых (равновесных) процессах
это равенство тождественно выполняется.
Для неравновесных процессов выполняется
основное неравенство термодинамики:
 .
.
