
- •Теория телетрафика
- •1.1. Теория телетрафика – одна из ветвей теории массового обслуживания
- •1.2. Математические модели систем распределения информации
- •1.3. Основные задачи теории телетрафика
- •1.4. Общие сведения о методах решения задач теории телетрафика
- •1.5. Краткий исторический обзор развития теории телетрафика
- •Контрольные вопросы
- •2.1. Основные понятия
- •2.2. Принципы классификации потоков вызовов
- •2.3. Характеристики потоков вызовов
- •2.4. Простейший поток вызовов
- •2.5. Нестационарный и неординарный пуассоновские потоки
- •2.6. Потоки с простым последействием
- •2.7. Симметричный и примитивный потоки
- •2.8. Поток с повторными вызовами
- •2.9. Поток с ограниченным последействием. Поток Пальма
- •2.10. Просеивание потоков. Потоки Эрланга
- •2.11. Длительность обслуживания
- •2.12. Поток освобождений
- •Контрольные вопросы
- •3.1. Поступающая, обслуженная, потерянная нагрузки
- •3.2. Концентрация нагрузки
- •3.3. Основные параметры и расчет интенсивности нагрузки
- •3.4. Характеристики качества обслуживания потоков вызовов
- •3.5. Пропускная способность коммутационных систем
- •Контрольные вопросы
- •4.1. Обслуживание вызовов симметричного потока с простым последействием
- •4.2. Обслуживание вызовов простейшего потока
- •4.3. Обслуживание вызовов примитивного потока
- •Контрольные вопросы
- •5.1. Обслуживание вызовов простейшего потока при показательном законе распределения длительности занятия
- •5.2. Обслуживание вызовов простейшего потока при постоянной длительности занятия
- •5.3. Область применения систем с ожиданием
- •Контрольные вопросы
- •6.1. Постановка задачи
- •6.2. Предельная величина интенсивности поступающей нагрузки
- •6.3. Уравнения вероятностей состояний системы с повторными вызовами
- •6.4. Основные характеристики качества работы системы с повторными вызовами
- •Контрольные вопросы
- •7.1. Общие сведения
- •7.2. Моделирование случайных величин
- •7.3. Моделирование коммутационных систем на универсальных вычислительных машинах
- •7.4. Точность и достоверность результатов моделирования
- •Контрольные вопросы
- •8.1. Общие сведения
- •8.2. Некоторые характеристики неполнодоступных схем
- •8.3. Выбор структуры ступенчатой неполнодоступной схемы
- •8.4. Выбор структуры равномерной неполнодоступной схемы
- •8.5. Построение цилиндров
- •8.6. Идеально симметричная неполнодоступная схема
- •8.7. Формула Эрланга для идеально симметричной неполнодоступной схемы
- •8.8. Априорные методы определения потерь в неполнодоступных схемах
- •8.9. Инженерный расчет неполнодоступных схем
- •Контрольные вопросы
- •9.1. Общие сведения
- •9.2. Комбинаторный метод. Полнодоступное включение выходов
- •9.3. Потери в двухзвеньевых схемах при отсутствии сжатия и расширения
- •9.4. Потери в двухзвеньевых схемах при наличии сжатия или расширения
- •9.5. Двухзвеньевые неполнодоступные схемы
- •9.6. Метод эффективной доступности
- •9.7. Структура многозвеньевых коммутационных схем
- •9.8. Способы межзвеньевых соединений и методы искания в многозвеньевых схемах
- •9.9. Расчет многозвеньевых коммутационных схем в режиме группового искания. Метод клигс
- •9.10. Метод вероятностных графов
- •9.11. Оптимизация многозвеньевых коммутационных схем
- •Контрольные вопросы
- •10.1. Качество обслуживания на автоматически коммутируемых сетях связи
- •10.2. Расчет нагрузок на входах и выходах ступеней искания коммутационных узлов
- •10.3. Расчет нагрузок, поступающих на регистры и маркеры
- •10.4. Способы распределения нагрузки
- •10.5. Колебания нагрузки. Расчетная интенсивность нагрузки
- •Контрольные вопросы
- •11.1. Общие сведения
- •11.2. Обходные направления и использование метода эквивалентных замен при расчете числа линий в обходных пучках
- •11.3. Динамическое управление. Характер задач, возникающих при управлении потоками
- •11.4. Кроссовая коммутация как управление структурой сети
- •11.5. Метод укрупнения состояний пучков при определении характеристик управляющей информации
- •Контрольные вопросы
- •12.1. Цели и задачи измерений
- •12.2. Принципы измерений параметров нагрузки и потерь
- •12.3. Обработка результатов измерений
- •12.4. Определение объема измерений
- •Контрольные вопросы
- •Список литературы
8.7. Формула Эрланга для идеально симметричной неполнодоступной схемы
Рассмотрим следующую модель:
в выходы одвозвеньевой идеально симметричной неполнодоступной схемы с доступностью d включено линий;
на входы схемы поступает простейший поток вызовов с параметром ;
длительность обслуживания является случайной величиной, распределенной по показательному закону F(t)=1–е–t;
если вызов поступает от источника нагрузочной группы, в которой нет доступа к свободной линии (все d линий заняты), то вызов теряется. Требуется определить вероятность потерь.
Как было указано в гл. 4, для любого однородного транзитивного марковского процесса с конечным числом состояний переходныe вероятностиpji(t) того, что система, находившаяся в состоянииj, за времяt перейдет в состояниеi, имеют предел, не зависящий от начального состоянияj. ЕслиV(t) –число занятых линий в неполнодоступном пучке в момент времениt, тоV(t) является случайным процессом с конечным числом состояний, поскольку число линий в НС конечно.
П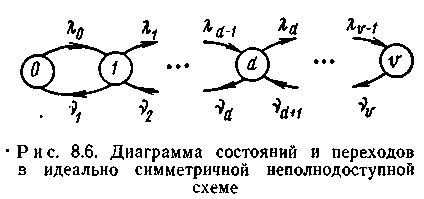 роцессV(t) является марковским, так как
будущее течение его не зависит от
прошлого, если известно настоящее, т.
е. известно V(t0). Кроме того,
этот процесс является однородным,
поскольку переходные вероятностирji(t)
зависят лишь от длины интервалаt=t2–t1 и не зависят
от расположения интервала на оси времени
(т. е. отt2иt1). И,
наконец,V(t) является транзитивным
марковским процессом. Это следует из
того, что возможен переход из любого
состоянияjв любое состояниеi
пучка. Иначе говоря, переходная
вероятностьpji(t) отлична
от нуля. Последнее можно подтвердить
следующими соображениями. Если разбить
интервалt на две части, то вероятность
перехода из состоянияjв нулевое
состояние за первую часть интервала
при условии, что не поступит ни одного
вызова и освободятся всеjзанятых
линий пучка, будет отлична от нуля. Точно
так же вероятность перехода системы из
нулевого состояния в состояниеi (если
произойдетi занятий и ни одного
освобождения) за вторую часть интервала
будет также отлична от нуля. Переходная
вероятностьPji(t) не
меньше произведения вероятностей
переходов из состоянияjв нулевое
состояние и из нулевого состояния в
состояниеi и поэтому отлична от
нуля.
роцессV(t) является марковским, так как
будущее течение его не зависит от
прошлого, если известно настоящее, т.
е. известно V(t0). Кроме того,
этот процесс является однородным,
поскольку переходные вероятностирji(t)
зависят лишь от длины интервалаt=t2–t1 и не зависят
от расположения интервала на оси времени
(т. е. отt2иt1). И,
наконец,V(t) является транзитивным
марковским процессом. Это следует из
того, что возможен переход из любого
состоянияjв любое состояниеi
пучка. Иначе говоря, переходная
вероятностьpji(t) отлична
от нуля. Последнее можно подтвердить
следующими соображениями. Если разбить
интервалt на две части, то вероятность
перехода из состоянияjв нулевое
состояние за первую часть интервала
при условии, что не поступит ни одного
вызова и освободятся всеjзанятых
линий пучка, будет отлична от нуля. Точно
так же вероятность перехода системы из
нулевого состояния в состояниеi (если
произойдетi занятий и ни одного
освобождения) за вторую часть интервала
будет также отлична от нуля. Переходная
вероятностьPji(t) не
меньше произведения вероятностей
переходов из состоянияjв нулевое
состояние и из нулевого состояния в
состояниеi и поэтому отлична от
нуля.
В общем случае неполнодоступная схема, в выходы которой включено линий, имеет 2микросостояний. Для идеально симметричной схемы достаточно рассмотреть только+1 макросостояний аналогично тому, как это имеет место для полнодоступного пучка.
Запишем параметры потоков рождения и гибели (занятий и освобождений линий) для рассматриваемого процесса (рис. 8.6). Так как на входы схемы поступает простейший поток вызовов, то при i<d 0== ... =d-1=. Переход из состоянияd в состояниеd+1 возможен только в том случае, если вызов поступает от источника нагрузочной группы, в которой не занята хотя бы одна изd доступных линий. Если же вызов поступит от источника нагрузочной группы, в которой заняты всеd доступных линий, то вызов теряется. Обозначим черезi условную вероятность потери вызова приi занятых линиях. В идеально симметричной неполнодоступной схеме приi<d i=0, а приid i>0. Тогда вероятность того, что в состоянииiпоступивший вызов займет свободную линию, будет равна 1–i.
Следовательно, для id i,=(1–i). Таким образом,

Параметр потока освобождений
![]()
По аналогии с (4.12) при конечном числе состояний стационарные вероятности состояний определяются следующими выражениями:

Подставляя (8.16) и (8.17) в (8.18) и учитывая, что для i<.d i=0, получим

Для получения выражения для вероятности потерь воспользу-
емся формулой полной вероятности:
![]()
Так как при i<d i=0, то
![]()
Подставляя в (8.20) выражение для рi из (8.19), получим

В
(8.21)
![]() приx<d. Для того чтобы
воспользоваться (8.21), необходимо вычислитьi.
приx<d. Для того чтобы
воспользоваться (8.21), необходимо вычислитьi.
В общем случае для произвольной НС условные вероятности iзависят не только от числаi занятых выходов, но и от интенсивности поступающей нагрузки, структуры НС и алгоритма установления соединения. Для практически используемых НС определение условных вероятностейiпредставляет собой сложную комбинаторную задачу. Определение всехi в данном случае практически невозможно из-за большого числа состояний системы.
Особое место среди НС занимают идеально симметричные неполнодоступные схемы, так как в этих схемах число нагрузочных групп g=Cd и занятиеd фиксированных линий блокирует одну определенную нагрузочную группу (Cdd=l).
Определим для идеально симметричной схемы число нагрузочных групп, блокируемых в состоянии i занятых выходов, еслиid. Очевидно, что число заблокированных групп равно числу способов выбораd выходов изi занятых выходов, т. е.Cdi. Следовательно, условная вероятность того, что приi занятых выходах идеально симметричной НС поступающий вызов попадает в заблокированную группу, равна отношению числа заблокированных групп к общему числу групп. Поэтому условная вероятность блокировкиi будет равна
![]()
Соотношение (8.22) справедливо, если возможные размещения свободных и занятых линий равновероятны, что имеет место в силу симметрии идеальной НС. Подставляя выражение для iв формулу для потерь (8.21), получим

Эта формула называется формулой Эрланга для идеально симметричной неполнодоступной схемы. Иногда ее называют третьей формулой Эрланга и обозначаютB,d(у). Формула (8.23) табулирована [30].
