7.3. Моделирование коммутационных систем на универсальных вычислительных машинах

Моделирование на основе цепи Маркова процесса обслуживания потока вызовов коммутационной системой. При моделировании процесса обслуживания потока вызовов коммутационной системой, как и при моделировании любой системы массового обслуживания, нет необходимости полностью имитировать реальный процесс. Достаточно, чтобы различные состояния искусственного и реального процессов совпадали либо находились во взаимно однозначном соответствии, иными словами, достаточно, чтобы моделируемый искусственный процесс и получаемые при этом характеристики соответствовали в статистическом смысле реальному процессу и исследуемым вероятностным характеристикам.

Ранее было показано, что процесс функционирования любойкоммутационной системы при обслуживании потока с простымпоследействием (в том числе и простейшего потока вызовов) припоказательном распределении длительности занятия является марковским процессом. Поэтому вместо моделирования реальногопроцесса обслуживания потока вызовов коммутационной системойможно моделировать марковский процесс, т. е. моделировать искусственный процесс с вероятностными свойствами реального процесса. При этом модель описывается системой уравнений различных состояний обслуживающей коммутационной системы. Заменамоделирования реального процесса моделированием марковскогопроцесса приводит к существенной экономии в оперативной и постоянной памяти вычислительной машины.

При имитации моделирования реального процесса обслуживающей коммутационной системы марковским процессом требуется учитывать случайные отрезки времени пребывания системы в различных состояниях. Существенное дальнейшее упрощение статистического моделирования обслуживающей коммутационной системы достигается заменой моделирования марковского процесса моделированием цепи Маркова. При этом переход модели из одного состояния в другое происходит в дискретные моменты времени, в каждый из которых реализация случайной величины имитирует либо поступление нового вызова, либо окончание находящегося на обслуживании какого-либо вызова. Между всеми состояниями коммутационной системы и моделируемой цепи Маркова устанавливается взаимно однозначное соответствие. Это означает, что под воздействием поступившего в дискретный момент времени вызова (или окончания соединения) переход моделируемой цепи Маркова из какого-либо определенного состояния в новое соответствует переходу реальной коммутационной системы в такое же новое состояние, если до этого коммутационная система находилась в однозначном состоянии с моделируемой цепью Маркова.

При моделировании цепи Маркова каждое изменение цепи происходит за один цикл работы машины, в течение которого реализуется случайная величина, имитирующая поступление нового вызова или окончание обслуживания какого-либо ранее поступившего вызова, а также происходит переход цепи в другое состояние. Не требуется в явном виде учитывать время пребывания системы в различных состояниях. В результате уменьшаются объемы информации, которые должны храниться в памяти машины, на каждое изменение состояния обслуживающей системы требуется меньшее число операций машины – сокращается время цикла работы машины. Поэтому имеется возможность осуществлять на ЭВМ статистическое моделирование обслуживающих коммутационных параметров, получать значительные по объему статистические характеристики исследуемых систем и одновременно сокращать время моделирования. Для реализации каждого из событий, поступающих в дискретные моменты времени (поступления нового вызова, освобождения какого-либо соединительного пути), необходимо знать вероятности их поступления. С этой целью определим указанные вероятности и способ их реализации при моделировании на ЭВМ цепи Маркова, имитирующей обслуживающую коммутационную систему при достаточно общих предположениях.

Коммутационная система произвольной структуры (рис. 7.3) содержит s групп входов иh групп (направлений) выходов. На каждую группу входов поступает поток с простым последействием.

Параметр потока вызовов – (i, j, k), гдеi – номер группы входов;j– номер выбираемого направления;k – номер состояния коммутационной системы в момент поступления вызова. Параметр потока освобождений соединительного пути междуi-й группой входов иj-м направлением приk-м состоянии системы –(i, j, k). Суммарный параметр потоков вызовова_kи суммарный параметр потоков освобожденийb_k в промежутки времени, в которые коммутационная система находится в состоянииk, составляют

При k-м состоянии цепи Маркова моделируется случайная величина, равномерно распределенная на отрезке [0,a_k+b_k). Если в рассматриваемом цикле работы ЭВМ случайная величинареализуется на участке равномерно распределенного отрезка [0,а_k+b_k), соответствующем

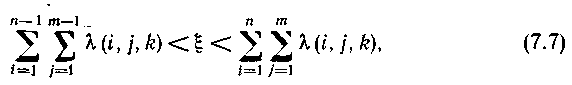
то полагаем, что эта случайная величина определяет поступление вызова на п-ю группу входов и соединение требуется установить вm-м направлении. Еслиреализуется на участке

то величина определяет освобождение соединительного пути междуn-й группой входов ит-й группой выходов. Заметим, что при этом может освободиться любой из установленных соединительных путей между указанными группами входов и выходов.

Статистические характеристики моделирования. Целью моделирования является получение статистических оценок вероятностных характеристик процессов обслуживания коммутационными системами поступающих потоков вызовов при заданных дисциплинах обслуживания. Эти оценки принято называтьстатистическими характеристиками. К таким характеристикам относятся: в системах с потерями – вероятность потерь, вероятности различных состояний коммутационной системы; в системах с ожиданием – распределение времени ожидания начала обслуживания, среднее время ожидания, средняя длина очереди и другие характеристики.

Моделирование исследуемого процесса разбивается на группу п экспериментов (серий), в каждом из которых производится равное числоm испытаний (например, число поступающих вызовов).

Число испытаний в каждом эксперименте выбирается таким, чтобы измеряемые статистические характеристики исследуемых вероятностных величин были бы достаточно представительны. Так, при определении вероятности потерь (ожидаемая величина которых составляет порядка 5%o) необходимо в каждом эксперименте предусмотреть десять и более тысяч испытаний, с тем чтобы число потерянных вызовов достигало нескольких десятков и даже сотен. В конце моделирования исследуемого процесса определяются средние значения, дисперсии и доверительные интервалы измеряемых статистических характеристик.

Перед моделированием первого эксперимента необходимо осуществить нулевую серию моделирования для приведения исследуемой системы в стационарный режим.