Контрольные вопросы

1. В каких единицах измеряются нагрузка и интенсивность нагрузки?

2. Сформулируйте теорему о количественной оценке интенсивности обслуженной нагрузки.

3. Сформулируйте теорему о количественной оценке интенсивности поступающей нагрузки.

4. Дайте определение часа наибольшей нагрузки, поясните способ определения интенсивности нагрузки в ЧНН.

5. Что такое коэффициент концентрации нагрузки?

6. По каким признакам различают категории источников телефонной нагрузки?

7. Каким параметром оценивается уровень удовлетворения потребностей в телефонной связи?

8. Какими результатами может окончиться поступающий на АТС вызов?

9. Какое отношение числа состоявшихся разговоров к числу поступивших на АТС вызовов следует считать удовлетворительным?

10. Какие показатели используются для количественной оценки качества обслуживания с явными потерями и с ожиданием?

11. Дайте простейшую классификацию дисциплин обслуживания поступающих вызовов.

12. От каких параметров зависит пропускная способность коммутационной системы?

13. Почему при фиксированной величине потерь с ростом интенсивности поступающей на пучок линий нагрузки, создаваемой простейшим потоком вызовов, возрастает среднее использование одной линии пучка?

ГЛАВА ЧЕТВЕРТАЯ

Полнодоступный пучок. Система с потерями

4.1. Обслуживание вызовов симметричного потока с простым последействием

Постановка задачи. Исходными данными модели являются: неблокирующая коммутационная система (никаких других ограничений на структуру системы не накладывается – она может быть однозвеньевой или многозвеньевой);

в выходы коммутационной системы включен полнодоступный пучок емкостью (1<) линий (приборов);

вызовы, поступающие на входы коммутационной системы, образуют симметричный поток с простым последействием с параметром _i;

дисциплина обслуживания коммутационной системой поступающего потока вызовов – с потерями;

длительность обслуживания Т коммутационной системой вызова является случайной величиной, распределенной по показательному закону, т. е. функция распределения длительности занятия

где – параметр длительности занятия. Обычно за единицу времени принимается средняя длительность занятия – 1/=1, следовательно, и=1.

Задача формулируется следующим образом. Полнодоступный пучок емкостью  линий, включенных в выходы неблокирующей коммутационной системы с потерями, обслуживает вызовы, образующие симметричный поток с простым последействием с параметром_i. Длительность обслуживания вызова коммутационной системой распределена по показательному закону. Требуется определить вероятности различных состояний полнодоступного пучка в процессе обслуживания поступающих вызовов.

В этой задаче достаточно исследовать макросостояния системы, т. е. состояния, различающиеся числом iодновременно занятых линий в любой момент времени (i= 0, 1, 2,...,), независимо от того, какие именно линии заняты. Это объясняется следующими соображениями.

1. При любом состоянии полнодоступного пучка линий, включенных в выходы неблокирующей коммутационной системы, т. е. при любом числе занятых линий, независимо от того, какие именно линии заняты, любой поступивший вызов может быть обслужен любой из свободных в данный момент линий пучка. Поступивший вызов получает отказ в обслуживании (теряется) только в тех случаях, когда в момент поступления вызова все  линий пучка заняты. Указанное свойство полнодоступного пучка не зависит ни от структуры полнодоступного пучка (прямое или сдвинутое включение линий пучка в объединяемые выходы коммутационной системы), ни от способа искания свободной линии пучка (с исходного положения, в случайном или любом другом порядке) .

2. Пучок линий обслуживает вызовы симметричного потока, параметр которого _i, зависит в любой момент времени только от состояния данного пучка. Параметр_iзадается какой-либо зависимостью лишь от числа занятых (или от числа свободных) линий и не зависит от того, какие именно линии пучка заняты.

Из этих соображений следует, что вероятности занятости фиксированного числа линий не зависят от того, какие именно линии заняты, а зависят только от числа занятых линий. Определим вероятности различных макросостояний системы – вероятности того, что в системе в момент времени t занято точноi линий пучка (i=0, 1, 2,...,)–p_i(t). Помимо того, определим вероятности потерь по времениp_t и по вызовамр_в.

Число занятых линий i в моментt является случайным. Поэтому процесс изменения числа занятых линий во времени является случайным процессом. Если известно, что в моментtзанятоi линий, то последующее течение процесса изменения числа занятых линий в вероятностном смысле зависит только от моментов появления новых вызовов и от моментов окончания занятий линий как вызовами, поступившими до моментаt, так и новыми вызовами.

Моменты появления новых вызовов не зависят от рассматриваемого случайного процесса до момента t, так как параметр_i поступающего на систему симметричного потока вызовов зависит только от числаi занятых линий в рассматриваемый моментt. Также от течения процесса до моментаt не зависят и моменты окончания занятий линий. Последнее следует из показательного распределения длительности занятий, при котором время оставшейся части занятия не зависит от того, сколько времени оно уже продолжается (основное свойство показательного распределения).

Отсюда рассматриваемый случайный процесс обладает следующим свойством: если известно число занятых линий в момент времени t, то процесс изменения состояний системы после моментаt в вероятностном смысле не зависит от течения процесса до этого момента, т. е. рассматриваемый процесс являетсямарковским.

Понятие о марковских процессах. Для марковских процессов, названных в честь выдающегося русского математика А. А. Маркова (1856–1922 гг.), будущее определяется известным настоящим и не зависит от прошлого.

Пусть V(t) –число занятых линий в момент времениt. Если в некоторый моментt в системе занятоi линий (система находится в состоянииi), тоV(t)=i, i= 0, 1, 2,...,. Система имеет конечное число (+1) состояний, и рассматриваемый марковский процесс является процессом с конечным числом состояний. Обозначим черезp_ji(t₁, t₂) вероятность того, что система, находившаяся в моментt₁ в состоянииj, за время [t₁, t₂) перейдет в состояниеi. Рассматриваемый случайный процесс, т. е. процесс поступления вызовов и освобождений, зависит лишь от числа занятых линийjв начальный моментt₁ и от длины отрезка времени [t₁,t₂). Этот процесс не зависит от моментовt₁иt₂. Поэтому и вероятностьp_ji(t₁, t₂) зависит только от длины отрезка времени [t₁, t₂) и значенийjиi. Процессы Маркова, обладающие таким свойством, называютсяоднородными.

Выделим на отрезке времени [t₁, t₂) моментt_(t₁<t_<t₂). Для того чтобы за промежуток времени [t₁, t₂) система перешла из состоянияj, в котором она находилась в моментt₁, в состояниеi в моментt₂, система должна за отрезок времени [t₁, t_) перейти в некоторое состояниеr(0r), а потом за оставшийся отрезок времени [t_, t₂) –из состоянияrв состояниеi. По формуле полной вероятности получаем

Формула (4.1) называется уравнением Колмогорова–Чепмена. В силу свойства процесса Маркова вероятностьp_ri(t_, t₂) является безусловной, не зависящей от процесса, протекающего на отрезке времени [t₁, t_), так как известно, что в моментt_ система находится в состоянииr.

В формуле (4.1) изменим обозначения отрезков времени: [t₁, t₂) обозначим через [0,t+), тогда [t₁, t) будет [0,t) и[t₁, t₂)–[t, t+). При этом (4.1) преобразуется к виду

Для решения задачи обслуживания полнодоступным пучком вызовов симметричного потока удобно воспользоваться частным случаем процесса Маркова – процессом рождения и гибели.

Процесс рождения и гибели – это марковский процесс с непрерывным параметром t, имеющий конечное (0, 1, 2,...,i,..., ) или счетное (0, 1, 2, ...,i, ...)множество состояний, в каждом из которых за бесконечно малый промежуток времени [t, t+)с вероятностью более нуля возможен непосредственный переход системы только в соседнее состояние, иными словами, из состоянияi возможен либо непосредственный переход в состояниеi–1 илиi+1, либо система остается в состоянииi. При этом вероятность того, что за время0 произойдет более одного изменения состояния, равна().

Определение вероятностей состояния полнодоступного пучка.Не ограничивая пока емкости пучка линий (=), определим вероятностир_i(t+) того, что в момент (t+) пучок находится в состоянииi.

Так как симметричный поток является ординарным и параметр его в момент t не зависит от процесса обслуживания вызовов до моментаt, то процесс обслуживания вызовов данного потока полнодоступным пучком линий представляет собой процесс рождения и гибели. Диаграмма состояний и переходов этого процесса приведена на рис. 4.1.

Процесс рождения в рассматриваемой задаче отождествляется с процессом занятий, а процесс гибели – с процессом освобождений линий пучка. Параметры потоков занятий и освобождений обозначены соответственно _i, и_i,i=0, 1, 2,... Согласно процессу рождения и гибели, при0 пучок в момент (t+) может находиться в состоянииi только при наличии следующих условий.

1. В момент t пучок находится в состоянииi–1 (вероятность этого событияp_i-1(t)), и за времяна обслуживание поступит точно один вызов (вероятность данного событияр_в()). Тогда вероятность перехода пучка за промежуток времени [t, t+) из состоянияi–1 в состояниеi составляетp_i-1,i()=р_i-1(t)p_в(). При этом вероятностьр_в() является условной. Она определяется с учетом того, что в моментt пучок находился в состоянииi–1.

2. В момент t пучок находится в состоянииi+1 (вероятность этого событияp_i+1(t)), и за времяосвободится точно одна изi+1 занятых линий (вероятность этого событияp_{ос i+1}()). Вероятность перехода пучка за промежуток времени [t, t+) из состоянияi+l в состояниеi составляетр_i+1,i()=p_i+1(t)p_{ос i+1}(t). Вероятностьр_{ос i+1}() является условной, она определяется с учетом того, что в моментt пучок находился в состоянииi+1.

3. В момент t пучок находится в состоянииi (вероятность этого событияp_i (t)). За времяпучок не изменяет своего состояния, он остается в состоянииi, т. е. на пучок не поступает вызова и в нем не освобождается ни одна из занятых линий [вероятность этого события (1–p_в()–p_{oc i}())]. Вероятность перехода пучка из состоянияi в состояниеi составляетр_ii()=p_i(t)(1–р_в()–p_{oc i}()).

4. За время [t, t+) в пучке происходят два и более переходов в результате поступления двух и более вызовов, либо освобождения двух и более линий, либо поступления одного и более вызовов и одновременно освобождения одной и более линий. Вероятность таких событий составляето().

Условия 1–4 взаимно исключают друг друга, поэтому искомые вероятности р_i(t+), (i=0, 1, 2,..., определяются как сумма приведенных выше четырех вероятностей:

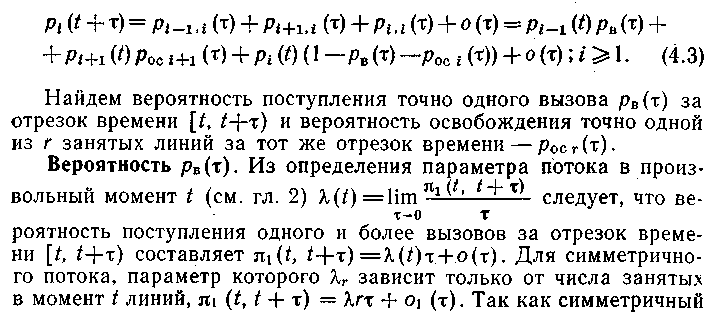
поток является ординарным, то вероятность поступления двух и более вызовов за бесконечно малый отрезок времени [t, t+] составляет₂(t, t+)=o₂(). Отсюдаp_в()=p₁(t, t+)–₂(t, t+)=_ro₁()–o₂(). Учитывая, чтоo₁() ио₂()–бесконечно малые одного порядка, получим

Вероятность p_{ос r}().Вероятность освобождения за время0 одной изrзанятых линий не зависит от характера поступающего потока вызовов. Вероятностьр_{oc r}() зависит только от состоянияr пучка в моментt и от закона распределения длительности обслуживания, который задан показательным. Вероятность освобождения хотя бы одной изrзанятых линий за промежуток временив соответствии с (2.45) равна

Так как в рассматриваемой задаче за единицу времени принята средняя длительность занятия, то =1. Поток освобождений является ординарным. Отсюда вероятность освобождения точно одной изrзанятых линий за отрезок времени [t,t+) при0 равна

Заметим, что вероятности р_в(), определяемые (4.1), так же как и вероятностир_{oc r}(), определяемые (4.6), пропорциональны. Следовательно, вероятности поступления за времялюбых двух и более событий (двух и более вызовов, или двух и более освобождений, или вызова и освобождения и т. д.) есть величины порядкао(). Из этого следует, что вероятностиp_ri(t, t+) перехода системы за отрезок времени [t, t+) из состоянияr в состояниеiпри |r–i|2 равныp_ri(t, t+)=о(), |r–i|2.

Подставим в систему ур-ний (4.3) полученные значения вероятностей р_в() иp_ос(), перенесем из правой части уравнений в левуюp_i(t), просуммируем все бесконечно малые слагаемыео() и разделим обе части уравнений на. В результате получим

Получаем для определения вероятностей p_i(t), i=0, 1, 2,..., систему дифференциальных уравнений

расходится, то вызовы поступают настолько чаще по сравнению с освобождениями занятых линий, что, начиная с некоторого момента времени, окажется невозможным обслуживание коммутационной системой поступающего потока вызовов. Для сходимости ряда необходимо, чтобы параметр потока вызовов _i существенно не отличался от параметра потока освобождений. Это условие выполняется в рассматриваемой задаче обслуживания полнодоступным пучком линий симметричного потока вызовов. Доказано, что при любомt (доказательство не приводится), если ряд сходится, то

В общем случае для процесса рождения и гибели со счетным множеством состояний с параметрами _i, и_i,i=0, 1, 2,..., стационарные вероятности состояний определяются следующими выражениями:

В рассматриваемой задаче обслуживания полнодоступным пучком емкостью  линий симметричного потока вызовов параметр потока вызовов_i и параметр потока освобождений_i=i конечны; число состояний также является величиной конечной, оно равно

При этом, если система находится в состоянии  (все линии заняты), то поступающие вызовы не могут производить новых занятий и, следовательно, дляi параметр потока занятий_i=0. В состоянииi=0 все линии свободны и параметр потока освобождений₀=0. С учетом этого вероятностир₀ ир_i(1i) определяются формулами

Определение вероятностей потерь по времени и потерь по вызовам. Вероятностьp_i можно рассматривать как долю времени (на промежуткеТ), в течение которого в пучке занято точноi линий. В частности, доля времени (на промежуткеТ), в течение которого заняты все линий полнодоступного пучка, равна вероятностиp_. Применительно к полнодоступному пучку линий, включенных в выходы неблокирующей коммутационной системы, вероятность потерь по времениp_t представляет собой долю времени (на промежуткеТ), в течение которого заняты все линий пучка, и определяется соотношением

Определим вероятность потерь по вызовам р_в. Согласно определениюр_в есть отношение интенсивности потерянного_п к интенсивности поступающегопотоков вызовов:p_в=_п/. Здесь

Следовательно,

(в целях идентичности с формулами p_i иp_t в (4.15) индекс суммированияiзаменен наj).