
Матан типовой
.doc
Введение
В третьем семестре студенты должны выполнить 3 контрольные работы по темам: «Кратные интегралы», «Криволинейные и поверхностные интегралы», «Ряды».
Порядковый номер задания соответствует выбранному варианту, номер которого определяет преподаватель. Количество и порядок решения заданий могут меняться по его усмотрению. Необходимые знания, понятия, правила излагаются на практических занятиях по курсу.
Задания, отмеченные одной звездочкой, требуют точного выполнения чертежа на миллиметровой бумаге или применения знаний по начертательной геометрии. Задания, отмеченные двумя звездочками, являются заданиями повышенной сложности и требуют объемных вычислений. И, наконец, задание, отмеченное тремя звездочками, требует применения компьютера.
По просьбе преподавателя задания, отмеченные звездочками, могут быть оформлены в виде рефератов или научных работ студентов.
Контрольная работа 10
Кратные интегралы
1*.Изменить порядок интегрирования:
1. а) ;
б)
;
б)

2. а)
 ; б)
; б)

3. а) ; б)
; б)

4. а)
 ;
б)
;
б)
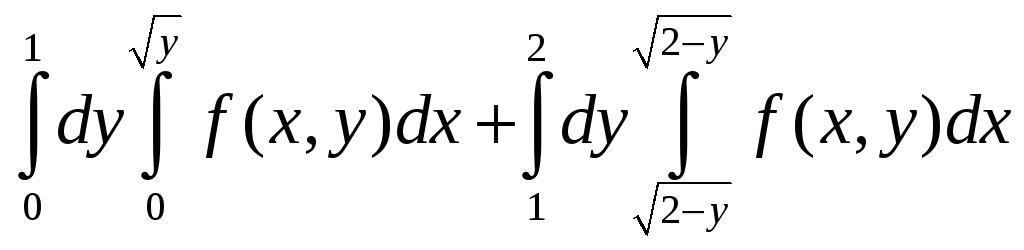
5. а) ;
б)
;
б)

6. а)
 ;
б)
;
б)

7. а)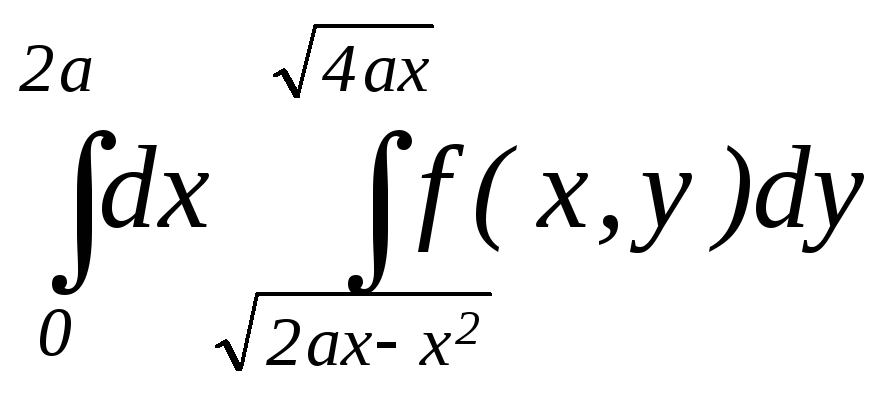 ; б)
; б)
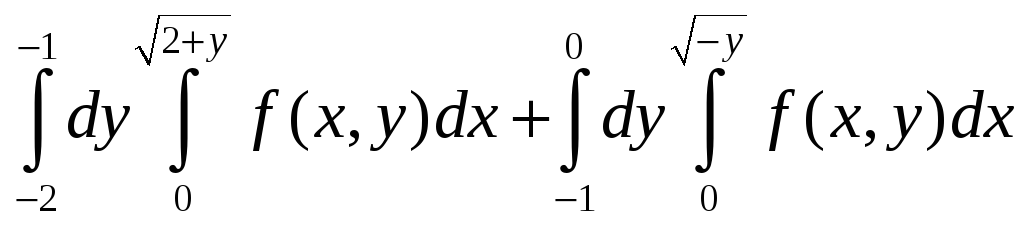
8. а)![]() ;
б)
;
б)
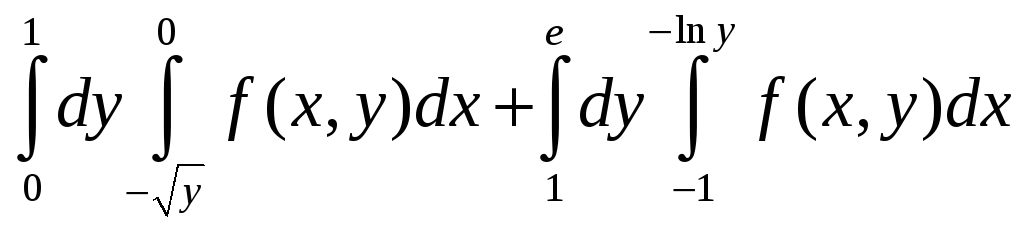
9. а) ;
б)
;
б)

10. а) ;
б)
;
б)

11. а) ;
б)
;
б)

12. а)![]() ;
б)
;
б)

13. а)![]() ;
б)
;
б)

14. а)![]() ;
б)
;
б)

15. а)![]() ;
б)
;
б)

16. а)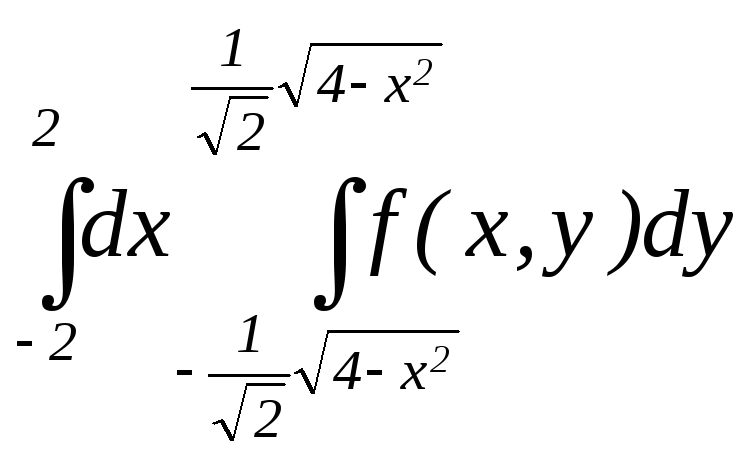 ;
б)
;
б)
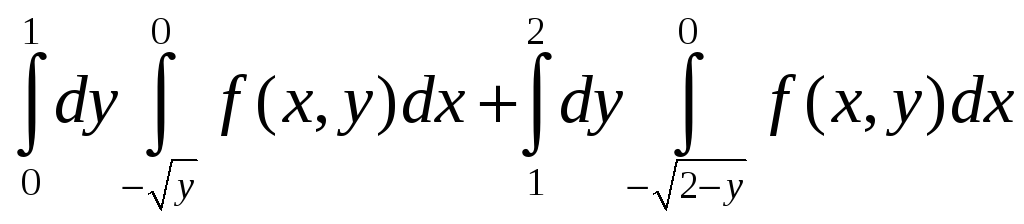
17. а) ;
б)
;
б)

18. а) ;
б)
;
б)

19. а)![]() ;
б)
;
б)

20. а) ;
б)
;
б)

21. а) ;
б)
;
б)

22. а) ;
б)
;
б)

23. а) ;
б)
;
б)
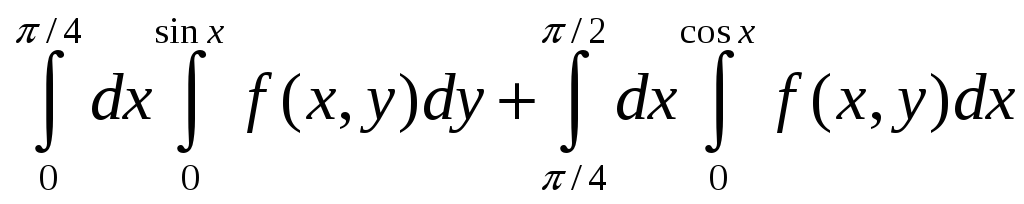
24. а)
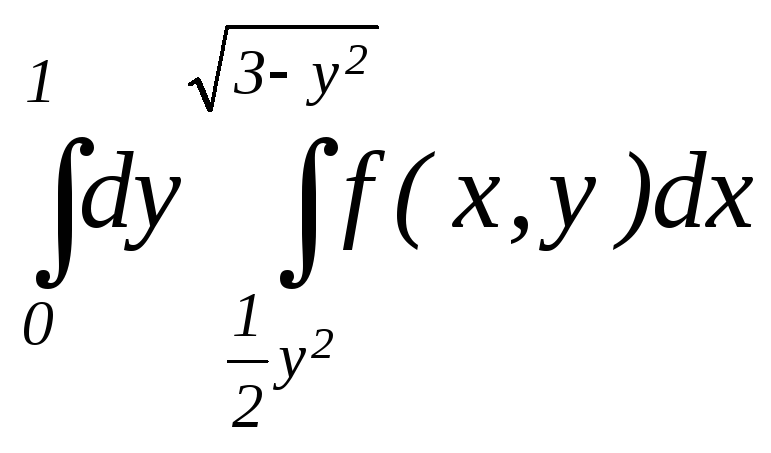 ;
б)
;
б)

25. а) ;
б)
;
б)

26. а) ;
б)
;
б)

27. а)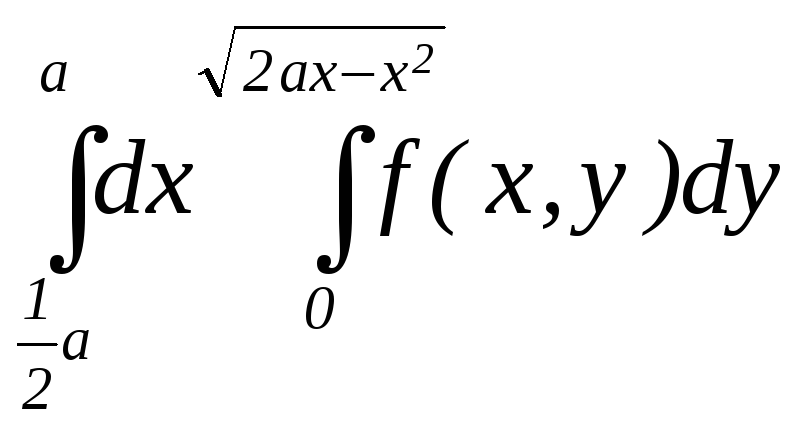 ;
б)
;
б)

28. а)
 ;
б)
;
б)

29. а)![]() ;
б)
;
б)

30. а)
 ;
б)
;
б)

2*.Вычислить двойные интегралы:
1.а)
![]() ,
где D:
x=0,
y=0,
,
где D:
x=0,
y=0,
![]() ;
;
б)
![]() ,
где D:
меньшая часть круга
,
где D:
меньшая часть круга
![]() ,
отсекаемая
,
отсекаемая
прямой y=x
2.а)
![]() ,
где D:
y=4,
y=x2,
,
где D:
y=4,
y=x2,
![]() (x>0);
(x>0);
б)
![]() ,
где D:
,
где D:
![]()
3.а)
![]() ,
где D:
x=2,
y=x,
,
где D:
x=2,
y=x,
![]() ;
;
б)
![]() ,
где D:
,
где D:
![]()
4.а)
![]() ,
где D:
y-x=2,
y=x2
;
,
где D:
y-x=2,
y=x2
;
б)
![]() ,
где D:
верхняя часть области, ограниченная
линией
,
где D:
верхняя часть области, ограниченная
линией
![]() и полярной осью
и полярной осью
5.а)
![]() ,
где D:
,
где D:
![]() ,
y=x,
y=2-x2;
,
y=x,
y=2-x2;
б)
![]() ,
где D:
,
где D:
![]() ,
,
![]() ,
(y>0,
x>0)
,
(y>0,
x>0)
6.а)
![]() ,
где D:
треугольник с вершинами О(0;0),
,
где D:
треугольник с вершинами О(0;0),
А(1;-1), В(1;1);
б)
![]() ,
где D:
,
где D:
![]()
7.а)
![]() ,
где D:
y=1+x2
, y=5;
,
где D:
y=1+x2
, y=5;
б)
![]() ,
где D:
,
где D:
![]() ,
y=x,
,
y=x,
![]()
8.а)
![]() ,
где D:
x=y2
, y=x2;
,
где D:
x=y2
, y=x2;
б)
![]() ,
где D:
,
где D:
![]()
9.а)
![]() ,
где D:
x=0,
y=0,
x=1,
,
где D:
x=0,
y=0,
x=1,
![]() ;
;
б)
![]() ,
где D:
,
где D:
![]()
10.а)
![]() ,
где D:
x=1,
x=3,
y=x,
y=x2;
,
где D:
x=1,
x=3,
y=x,
y=x2;
б)
![]() ,
где D:
,
где D:
![]()
11.а)
![]() ,
где D:
треугольник с вершинами О(0;0), А(1;1),
В(0;1);
,
где D:
треугольник с вершинами О(0;0), А(1;1),
В(0;1);
б)
![]() ,
где D:
,
где D:
![]()
12.а)
![]() ,
где D:
треугольник с вершинами О(0;0), А(1;-1),
В(1;1);
,
где D:
треугольник с вершинами О(0;0), А(1;-1),
В(1;1);
б)
![]() ,
где D:
,
где D:
![]()
13.а)
![]() ,
где D:
y2=x,
x=0,
y=1;
,
где D:
y2=x,
x=0,
y=1;
б)
![]() ,
где D:
полукруг диаметром
,
где D:
полукруг диаметром
![]() с центром в точке
с центром в точке
![]()
14.а)
![]() ,
где D:
треугольник с вершинами О(0;0), А(10;1),
В(1;1);
,
где D:
треугольник с вершинами О(0;0), А(10;1),
В(1;1);
б)
![]() ,
где D:
,
где D:
![]()
15.а)
![]() ,
где D:
x2+(y-1)2=1,
x+y=2,
,
где D:
x2+(y-1)2=1,
x+y=2,
![]() ;
;
б)
![]() ,
где D:
,
где D:
![]() (область, не содержащая полюса)
(область, не содержащая полюса)
16.а)
![]() ,
где D:
x=1,
x=2,
y=x,
y=x2
;
,
где D:
x=1,
x=2,
y=x,
y=x2
;
б)
![]() ,
где D:
,
где D:
![]()
17.а)
![]() ,
где D:
,
где D:
![]() ;
;
б)
![]() ,
где D:
,
где D:
![]()
18.а)
![]() ,
где D:
x=0,
x=,
y=0,
y=1+cosx;
,
где D:
x=0,
x=,
y=0,
y=1+cosx;
б)
![]() ,
где D:
,
где D:
![]()
19.а)
![]() ,
где D:
y=
,
где D:
y=![]() ,
y=-
,
y=-![]() ,
x=0,
x=3cosy;
,
x=0,
x=3cosy;
б)
![]() ,
где D:
,
где D:
![]()
20.а)
![]() ,
где D:
x=0,
x=
,
где D:
x=0,
x=![]() ,
y=1,
y=cosx;
,
y=1,
y=cosx;
б)
![]() ,
где D:
,
где D:
![]()
21.а)
![]() ,
где D:
y2
=2x,
x=1;
,
где D:
y2
=2x,
x=1;
б)
![]() ,
где D:
,
где D:
![]()
22.а)
![]() ,
где D:
y=2-x2
, y=2x-1;
,
где D:
y=2-x2
, y=2x-1;
б)
![]() ,
где D:
,
где D:
![]()
23.а)
![]() ,
где D:
x=0,
x=2,
y=0,
y=a;
,
где D:
x=0,
x=2,
y=0,
y=a;
б)
![]() ,
где D:
,
где D:
![]() .
.
24.а)
![]() ,
где D:
x=0,
x=1,
y=x,
y=2x;
,
где D:
x=0,
x=1,
y=x,
y=2x;
б)
![]() ,
где D:
x=0,
x=1,
y=0,
,
где D:
x=0,
x=1,
y=0,
![]()
25.а)
![]() ,
где D:
x=1,
x=3,
y=x,
y=x3
;
,
где D:
x=1,
x=3,
y=x,
y=x3
;
б)
![]() ,
где D:
,
где D:
![]()
26.а)
![]() ,
где D:
xy=1,
y=
,
где D:
xy=1,
y=![]() ,
x=2;
,
x=2;
б)
![]() ,
где D:
,
где D:
![]()
27.а)
![]() ,
где D:
x=0,
y=0,
4x+4y-=0;
,
где D:
x=0,
y=0,
4x+4y-=0;
б)
![]() ,
где D:
,
где D:
![]()
28.а)
![]() ,
где D:
y=x2
, y2
=x;
,
где D:
y=x2
, y2
=x;
б)
![]() ,
где D:
,
где D:
![]()
29.а)
![]() ,
где D:
x=2,
y=x,
xy=1;
,
где D:
x=2,
y=x,
xy=1;
б)
![]() ,
где D:
,
где D:
![]()
30.а)
![]() ,
где D:
y=1,
y=2,
x=0,
x=lny;
,
где D:
y=1,
y=2,
x=0,
x=lny;
б)
![]() ,
где D:
полукруг диаметром 2 с центром в точке
С(1;0).
,
где D:
полукруг диаметром 2 с центром в точке
С(1;0).
3*. Вычислить тройные интегралы:
1.а)
![]() ,
где V:
x=0,
y=0,
z=0,
x+y=1,
x2+z2=1
;
,
где V:
x=0,
y=0,
z=0,
x+y=1,
x2+z2=1
;
б)
![]() ,
где V:
z=x2+y2,
z=4
,
где V:
z=x2+y2,
z=4
2.а)
![]() ,
где V:
x2+y2+z2=1,
,
где V:
x2+y2+z2=1,
![]() ;
;
б)
![]() ,
где V:
x2+z2=1,
y=0,
y=1
,
где V:
x2+z2=1,
y=0,
y=1
3.а)
![]() ,
где V:
x=1,
x=3,
y=0,
y=2,
z=2,
z=5;
,
где V:
x=1,
x=3,
y=0,
y=2,
z=2,
z=5;
б)
![]() ,
где V:
3z=x2+y2,
z=3
,
где V:
3z=x2+y2,
z=3
4.а)
![]() ,
где V:
x=0,
y=0,
z=0,
x+y+z=1;
,
где V:
x=0,
y=0,
z=0,
x+y+z=1;
б)
![]() ,
где V:
2z=x2+y2,
z=2
,
где V:
2z=x2+y2,
z=2
5.а)
![]() ,
где V:
x=0,
y=1,
z=0,
y=3,
x+2z=3;
,
где V:
x=0,
y=1,
z=0,
y=3,
x+2z=3;
б)
![]() ,
где V:
x2+y2-2x=0,
z=0,
z=5
,
где V:
x2+y2-2x=0,
z=0,
z=5
6.а)
![]() ,
где V:
,
где V:
![]() ,
y=x,
y=2x
;
,
y=x,
y=2x
;
б)
![]() ,
где V:
x2+y2-z2
=0, z=2
,
где V:
x2+y2-z2
=0, z=2
7.а)
![]() ,
где V:
,
где V:![]() ;
;
б)
![]() ,
где V:
x2+y2-z2
=0, z=6-x2-y2,
z>0
,
где V:
x2+y2-z2
=0, z=6-x2-y2,
z>0
8.а)
![]() ,
где V:
x=0,
y=0,
z=0,
x=1,
y=1,
x+y+z=2;
,
где V:
x=0,
y=0,
z=0,
x=1,
y=1,
x+y+z=2;
б)
![]() ,
где V:
x2+y2=2x,
y=0, z=0, z=a, (a>0)
,
где V:
x2+y2=2x,
y=0, z=0, z=a, (a>0)
9.а)
![]() ,
где V:
x=0,
y=0,
z=0,
x=2,
y=2,
x+y+z=4;
,
где V:
x=0,
y=0,
z=0,
x=2,
y=2,
x+y+z=4;
б)
![]() ,
где V:
z=6-x2-y2,
x2+y2=z2,
z>0
,
где V:
z=6-x2-y2,
x2+y2=z2,
z>0
10.а)
![]() ,
где V:
x=0,
y=0,
x=1,
y=1,
z=0,
x+y+z=2;
,
где V:
x=0,
y=0,
x=1,
y=1,
z=0,
x+y+z=2;
б)
![]() ,
где V:
z=x2+y2,
z=4
,
где V:
z=x2+y2,
z=4
11.а)
![]() ,
где V:
x=0,
z=0,
y=1,
y=3,
x+2z=3;
,
где V:
x=0,
z=0,
y=1,
y=3,
x+2z=3;
б)
![]() ,
где V:
z2
=x2+y2,
z=1
,
где V:
z2
=x2+y2,
z=1
12.а)
![]() ,
где V:
x=0,
y=0,
z=0,
y=1,
x+z=1;
,
где V:
x=0,
y=0,
z=0,
y=1,
x+z=1;
б)
![]() ,
где V:
x2+y2=1,
z=0,
z=5
,
где V:
x2+y2=1,
z=0,
z=5
13.а)
![]() ,
где V:
x=0,
y=0,
z=0,
y=2,
x+z=3;
,
где V:
x=0,
y=0,
z=0,
y=2,
x+z=3;
б)
![]() ,
где V:
,
где V:
![]() ,
,
![]()
14.а)
![]() ,
где V:
x=1,
x=3,
y=0,
y=2,
z=2,
z=5;
,
где V:
x=1,
x=3,
y=0,
y=2,
z=2,
z=5;
б)
![]() ,
где V:
x2+y2=1,
2x+3z=6,
z=0
,
где V:
x2+y2=1,
2x+3z=6,
z=0
15.а)
![]() ,
где V:
x=1,
y=1,
z=0,
,
где V:
x=1,
y=1,
z=0,
![]() ;
;
б)
![]() ,
где V:
,
где V:
![]() ,
,
![]() ,
,
![]()
16.а)
![]() ,
где V:
x=0,
y=0,
z=3,
z=6,
x+y=1;
,
где V:
x=0,
y=0,
z=3,
z=6,
x+y=1;
б)
![]() ,
где V:
x2+y2+z2=1
,
где V:
x2+y2+z2=1
17.а)
![]() ,
где V:
x=0,
y=0,
z=0,
z=5,
x+y=1;
,
где V:
x=0,
y=0,
z=0,
z=5,
x+y=1;
б)
![]() ,
где V:
x2+y2=R2,
x2+y2+z2=R2,
z>0
,
где V:
x2+y2=R2,
x2+y2+z2=R2,
z>0
18.а)
![]() ,
где V:
x=0,
y=0,
z=0,
x+y=3,
x+y+z=5
;
,
где V:
x=0,
y=0,
z=0,
x+y=3,
x+y+z=5
;
б)
![]() ,
где V:
x2+z2=2y,
y=2
,
где V:
x2+z2=2y,
y=2
19.а)
![]() ,
где V:
x=0,
y=0,
z=0,
x=2,
z=2-y;
,
где V:
x=0,
y=0,
z=0,
x=2,
z=2-y;
б)
![]() ,
где V:
x2+y2=2x,
z=0, z=a (a>0)
,
где V:
x2+y2=2x,
z=0, z=a (a>0)
20.а)
![]() ,
где V:
,
где V:
![]() ;
;
б)
![]() ,
где
V:
x=0, z=0, x=1, z=a, x2+y2=1
,
где
V:
x=0, z=0, x=1, z=a, x2+y2=1
21.а)
![]() ,
где V:
x=0, y=0, z=0, y=a, x+z=a;
,
где V:
x=0, y=0, z=0, y=a, x+z=a;
б)
![]() ,
где V:
,
где V:
![]() ,
z=1
,
z=1
22.а)
![]() ,
где V:
x=0.5,
y=x,
y=2x,
z=0,
,
где V:
x=0.5,
y=x,
y=2x,
z=0,
![]() ;
;
б)
![]() ,
где V:
x2+y2=2x,
z=0,
z=1,
y=0
,
где V:
x2+y2=2x,
z=0,
z=1,
y=0
23.а)
![]() ,
где V:
x=0,
y=0,
z=0,
x+y+z=1;
,
где V:
x=0,
y=0,
z=0,
x+y+z=1;
б)
![]() ,
где V:
x2+y2=2x,
z=0,
z=3,
y=0
,
где V:
x2+y2=2x,
z=0,
z=3,
y=0
24.а)
![]() ,
где V:
x=0,
y=0,
z=0,
x+y+z=2;
,
где V:
x=0,
y=0,
z=0,
x+y+z=2;
б)
![]() ,
где V:
x2+y2=z2,
x2+y2+z2
=2Rz
,
где V:
x2+y2=z2,
x2+y2+z2
=2Rz
25.а)
![]() ,
где V:
,
где V:
![]() ;
;
б)
![]() ,
где V:
x2+y2-z2
=0, z=2
,
где V:
x2+y2-z2
=0, z=2
26.а)
![]() ,
где V:
x=0,
y=1,
z=0,
y=3,
x+2z=3;
,
где V:
x=0,
y=1,
z=0,
y=3,
x+2z=3;
б)
![]() ,
где V:
z=6-x2-y2,
x2+y2=z2
,
где V:
z=6-x2-y2,
x2+y2=z2
27.а)
![]() ,
где V:
x=0, y=0, z=0, y=a, x+z=b (a>0, b>0);
,
где V:
x=0, y=0, z=0, y=a, x+z=b (a>0, b>0);
б)
![]() ,
где V:
x2+y2+z2=4,
y=0,
2x2=x2+y2,
,
где V:
x2+y2+z2=4,
y=0,
2x2=x2+y2,
![]()
28.а)
![]() ,
где V:
x=0,
y=0,
z=0,
z=3,
x+y=1;
,
где V:
x=0,
y=0,
z=0,
z=3,
x+y=1;
б)
![]() ,
где V:
x2+y2=hz,
z=h.
,
где V:
x2+y2=hz,
z=h.
29.а)
![]() ,
где V:
x2+y2-z2
=1,
,
где V:
x2+y2-z2
=1,
![]() ;
;
б)
![]() ,
где V:
x2+y2=2z,
z=2.
,
где V:
x2+y2=2z,
z=2.
30.а)
![]() ,
где V:
,
где V:
![]() ;
;
б)
![]() ,
где V:
x2+z2=1,
y=0,
y=1.
,
где V:
x2+z2=1,
y=0,
y=1.
4*.С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями:
1.y=2-x, y2=4x+4 2. x=y2-2y, x+y=0
3.![]() (лемниската Бернулли) 4. y=4-x2,
y=0
(лемниската Бернулли) 4. y=4-x2,
y=0
5.
![]() (четырехлепестковая роза) 6.
(четырехлепестковая роза) 6.
![]() (трехлепестковая
роза)
(трехлепестковая
роза)
7.
![]() (кардиоида) 8. y2=4+x,
x+3y=0
(кардиоида) 8. y2=4+x,
x+3y=0
9.![]() (
четырехлепестковая роза) 10. xy=4,
y=x, x=4
(
четырехлепестковая роза) 10. xy=4,
y=x, x=4
11.
x2+y2=2x,
x2+y2=4x,
y=x,
![]() 12. y2=10x+25,
y2=-6x+9
12. y2=10x+25,
y2=-6x+9
