5. Корректировка полученных значений индексов оценки ситуации на основе полученных результатов

Полученные значения индексов на основе теоретических расчётов оценки ситуации по каждому из видов происшествий или событий должны периодически подвергаться проверке на соответствие. Должна рассматриваться ситуация, что теоретически рассчитанная величина индекса оценки ситуации для j-го вида транспортного происшествия соответствует его фактическому значению. Иными словами, правильно ли определена граница принятия первоочередных мер по предупреждению транспортных происшествий. В качестве альтернативы рассматривается ситуация, когда теоретически определённая величина индекса оценки ситуации дляj-го вида транспортного происшествияне соответствует фактическому, в результате транспортное происшествие j-го вида возникает до получения данных о необходимости принятия предупредительных мер. При этом требующей корректировки может считаться ситуация, когда фактическая величина индекса оценки ситуации, требующая принятия неотложных мер, меньше расчетной. В этой связи основанием для выполнения проверки правильности выполненного расчёта должно являться возникновение транспортных происшествий, исключая случаи, вызываемые природными явлениями катастрофического характера (землетрясения, ураганы, смерчи, наводнения, сходы лавин и т.п.), вандализмом и действиями террористического характера, а также являющиеся следствием особенностей физиологической природы человеческого организма, как указано во введении. При этом для выполнения проверки необходимо накопление данных по нескольким (не менее 4-5 случаев) транспортным происшествиям или событиям определённого вида, имевшим место по вине конкретного хозяйства.

Поскольку на первоначальном этапе было выдвинуто предположение о нормальном распределении случайной величины , то для проведения проверочного расчёта необходимо построить фактическое распределение случайной величины ,основываясь на практических данных о фактически имевших место транспортных происшествиях. Для этого выполняется расчет величин индексов оценки ситуации для каждого из произошедших транспортных происшествий порядком, описанным в пункте 4 настоящего документа. В итоге формируется выборка случайной величины , полученная эмпирическим путём. Для проверки правильности определения величины индекса оценки ситуации, требующей принятия первоочередных мер необходимо при заданном уровне значимости  последовательно проверить две гипотезы:

• о равенстве дисперсий двух нормально распределённых генеральных совокупностей (теоретически определённых и величин, полученных эмпирическим путём );

• о равенстве математических ожиданий двух нормально распределённых генеральных совокупностей (теоретически определённых и величин, полученных эмпирическим путём);

Для проверки представленных гипотез предлагается установить уровень достоверности равный 1-=0,9. В том случае, если обе гипотезы будут подтверждены при заданном уровне достоверности, нет необходимости для корректировки величины .

5.1. Проверка гипотезы о равенстве двух дисперсий нормально распределённых генеральных совокупностей

Для проверки данной гипотезы необходимо использовать критерий Фишера-Снедекора. Первоначально выдвигается основная гипотеза о равенстве дисперсий D() и D() случайных величин. Для этого для каждой из сформированных выборок случайных величин и определяются значения исправленных выборочных дисперсий по формуле:

(5.1)

где - текущее значение случайной величины;

- математическое ожидание случайной величины. В нашем случае математическое ожидание для дискретной случайной величины численно равно среднему арифметическому;

- коэффициент приведения выборочной дисперсии к несмещённому (нормальному) виду.

Далее определяется отношение полученных значений исправленных выборочных дисперсий для случайных величин и . По умолчанию для анализа рассматривается отношение большей дисперсии случайной величины к меньшей:

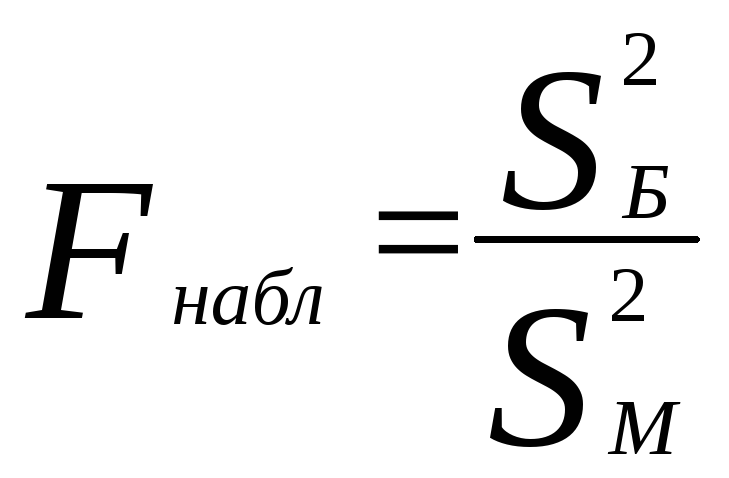(5.2)

где - наблюдаемое значение критерия;

- большая из исправленных выборочных дисперсий;

- меньшая из исправленных выборочных дисперсий.

Далее на основании специальных таблиц определяется критическая точка распределения Фишера-Снедекора по заданному уровню значимости =0,1 и степеням свободы k₁(случайной величины, имеющей большее значение исправленной выборочной дисперсии) и k₂ (случайной величины, имеющей большее значение исправленной выборочной дисперсии).

Значение степеней свободы k₁ определяется на единицу меньше длины выборок случайной величины, имеющей большее значение исправленной выборочной дисперсии. Аналогично, значение степеней свободы k₂ определяется на единицу меньше длины выборки случайной величины, имеющей меньшее значение исправленной выборочной дисперсии.

В том случае, если расчетное значение критерия больше критического<,нет оснований отвергать гипотезу о равенстве случайных величин. В противном случае > гипотеза о равенстве дисперсий отвергается.