МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-2»

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ

34

Под редакцией

доц. Т.В. ЗАХАРОВОЙ

Рекомендовано редакционно-издательским советом университета

в качестве методических указанийдля студентов специальностей

ИУИТ, ИСУТЭ, ИЭФ, ИТТОП, ИКБ, вечернего факультета

МОСКВА 2009

УДК 53:004

C-23

Физика. Методические указания к лабораторным работам 32, 132, 33, 133, 34, 42, 142 / Под ред. доц. Т.В. Захаровой.–М.: МИИТ, 2009.–84 с.

Методические указания соответствуют программе и учебным планам по курсу общей физики, в них представлены: краткая теория, задания к трём лабораторным работам по физике и методика их выполнения.

Авторы:	С.Г. Стоюхин– работы 32, 132
	Н.А. Гринчар, Т.В.Захарова– работы 33, 133
	Т.В. Захарова– работа 34
	А.В. Пауткина– работы 42, 142

©Московский государственный

университет путей сообщения

(МИИТ), 2009

Работа 34

Исследование дисперсии оптического стекла

Цель работы: определение показателя преломления оптического стекла для различных длин волн и построение кривой дисперсии.

Приборы и принадлежности: оптическая скамья, источник света в кожухе (лампа на парах ртути и неона), диафрагма в виде щели на кожухе источника света, коллиматор, гониометрический столик, зрительная труба, призма.

Введение

Дисперсией света называют явление зависимости показателя преломления среды (вещества) n от характеристик распространяющихся в нем электромагнитных волн светового диапазона: длины волны n  n(λ) или частоты n  n(ν). В вакууме λ  c/ν, где с – скорость света, λ – длина волны. В среде электромагнитные волны распространяются с фазовой скоростью , для них λ  /ν.

Показатель преломления среды определяется по формуле

n  , (1)

Величина дисперсии определяется параметрами

D_  илиD_  .

Дисперсия наблюдается практически во всех прозрачных средах, кроме вакуума, где скорость распространения электромагнитных волн любой длины одинакова. Дисперсия называется нормальной, если показатель преломления вещества монотонно возрастает с увеличением частоты ν (то есть убывает с увеличением λ) и аномальной в противном случае, когда показатель преломления с увеличением ν монотонно убывает (то есть n с увеличением λ растёт). Вдали от полос поглощения света веществом наблюдается нормальная дисперсия, а в пределах полос поглощения – аномальная. При использовании в экспериментах оптического стекла, прозрачного во всем спектральном диапазоне, дисперсия является нормальной.

Согласно теории Максвелла взаимодействие электрического и магнитного полей электромагнитной волны с веществом характеризуется параметрами среды  и  (диэлектрической и магнитной проницаемостями соответственно). Зависимости от этих параметров скорости распространения света в веществе выражается соотношением   , где₀, ₀ электрическая и магнитная постоянные, причём скорость света в вакууме с  . Учитывая соотношение (1), для показателя преломления можно записать:

n  . (2)

Таким образом, дисперсия должна обуславливаться совокупностью явлений, которые определяют зависимости от длины волны характеристик среды  и . Оптически прозрачные среды (к которым относится стекло) не магнитны (  1), поэтому в них дисперсия определятся только диэлектрическими свойствами данных сред:

n²    1  , (3)

где  - диэлектрическая восприимчивость среды.

Классическая электронная теория дисперсии учитывает молекулярное строение вещества и рассматривает молекулы как динамические системы, обладающие собственными частотами. Она дает объяснение явления на основе взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества (электронами, ионами) и совершающими вынужденные колебания в переменном электромагнитном поле волны [1  3]. Каждая молекула (или атом) вещества рассматривается как система линейных гармонических осцилляторов: заряженных частиц с разными эффективными зарядами q_i и массами m_i. Осцилляторы под действием электрического поля световой волны совершают вынужденные затухающие колебания с циклическими частотами _0і, и, таким образом, вносят вклад в поляризацию вещества. Дисперсия является следствием зависимости поляризации молекул (атомов) вещества от частоты.

В упрощённой модели рассматриваются незатухающие колебания только внешних, наиболее слабо связанных с ядром электронов, называемых оптическими. Предполагается, что диэлектрик состоит из атомов, на каждый атом приходится лишь один оптический электрон, и имеется лишь одна собственная циклическая частота свободных незатухающих колебаний ₀. В результате смещения электрона (заряд е), совершающего колебания в электрическом поле с напряженностью E, которая меняется по гармоническому закону E(t)  E₀ cost, атом приобретает электрический дипольный момент

e. (4)

Запишем формулу для поляризованности , которая, согласно определению, является векторной величиной, равной сумме дипольных моментов атомов единичного объема вещества:

. (5)

Для большого класса диэлектриков линейно зависит от напряжённости электрического поля. Если диэлектрик изотропный,

 ₀, (6)

причём   n₀, где  – поляризуемость атома, n₀ – концентрация поляризованных атомов. Из формул (3) – (6) следует, что

n²    1    1   1  . (7)

Дифференциальное уравнение вынужденных колебаний таких осцилляторов без учёта сопротивления (обусловленного поглощением энергии падающей волны) имеет вид

 ₀²r  , (8)

Его решением является гармоническая функция, описывающая смещение электрона в электрическом поле волны: r  r₀cost, где

r₀  . (9)

Подставив (9) в (7), получим зависимость показателя преломления среды n от циклической частоты ω:

n²  1  . (10)

Если в веществе имеются различные заряды q_i с массами m_i, совершающие вынужденные колебания с различными собственными частотами _0i, то

n²  1  . (11)

И

ω

з формулы (11) следует, что показатель преломленияn является функцией от  и должен характеризоваться «резонансным» поведением при совпадении собственных частот колебаний осцилляторов с вынуждающей частотой колебаний электрического поля электромагнитной волны.

Согласно формуле (11), при   _0i показатель преломления должен принимать значения n  ±∞. Однако на практике следует учитывать сопротивление среды колебаниям осцилляторов, а это приводит к тому, что реальная дисперсионная кривая n  n() приобретает вид, показанный на рис. 1 (на этом же рисунке приведена зависимость от частоты  коэффициента поглощения , который при резонансе принимает максимальное значение). В результате на резонансных частотах _0i оказывается не бесконечно большим, а лишь не слишком отличающимся от единицы.

В небольшом диапазоне значений  вблизи из резонансных частот наблюдается аномальная дисперсия: показатель преломления с ростом частоты уменьшается. В то же время в областях частот, далёких от _0i, с ростом  показатель преломления увеличивается, то есть наблюдается нормальная дисперсия. Таким образом, нормальная дисперсия света наблюдается вдали от полос (линий) поглощения света, аномальная дисперсия – в их пределах. Так как каждое вещество имеет присущие именно ему состав и структуру, для него будет наблюдаться набор характерных именно для этого вещества собственных циклических частот ₀₁, ₀₂, ₀₃… _0N. Выявление таких частот дает информацию о структуре молекул данного вещества.

Падающая на диэлектрик первичная световая волна возбуждает высокочастотные колебания молекул-диполей, которые излучают вторичную волну, распространяющуюся в среде с той же частотой, что и первичная волна, но с фазовой скоростью, характерной именно для этой среды. Вторичная волна также поглощается и переизлучается, возникает «третичная» волна, и т. д.: по мере распространения света в среде процесс повторяется снова и снова. Вследствие неодинаковости скоростей распространения волн между первичной и каждой из следующих волн возникает разность фаз. В итоге световая волна, распространяющаяся внутри диэлектрика (в данной работе – в стеклянной призме), а также на выходе из него является результатом наложения первичной и всех последующих излучаемых волн. Процесс поглощения-переизлучения занимает некоторое время, поэтому скорость распространения света в среде оказывается меньше, чем в вакууме, и при этом она зависит от характеристик колеблющихся диполей-осцилляторов,

Методы обнаружения явления дисперсии – любые методы, применяемые для определения показателя преломления (основанные на преломлении света в призмах, полном внутреннем отражении, на явлении интерференции). В данной работе измерение показателя преломления производится для оптического стекла, из которого изготовлена призма.

Спектральная призма и её характеристики

П

Рис.1

ростейшим оптическим прибором, удобным для изучения явления дисперсии, является трехгранная призма (рис. 2). Так как величина показателя преломления материала призмы зависит от, то лучи света разных длин волн падающего на призму светового пучка неодинаково преломляются уже на передней грани призмы. Это приводит к тому, что параллельный пучок белого света при своём проникновении в стекло сразу превращается в ряд цветных пучков, расходящихся веером, и на задней грани призмы наблюдается спектр.

Как правило, призма устанавливается в параллельных пучках лучей, поэтому для характеристики ее дисперсионных с

Рис.2

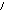
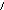
войств достаточно рассмотреть ход только одного из лучей падающего светового пучка.

Преломление луча в плоскости главного сечения призмы показано на рис. 2. Проходя через призму, световой луч отклоняется к её основанию и разлагается на монохроматические составляющие, при этом пучки с меньшей длиной световой волны отклоняется больше вследствие явления дисперсии.

Для оптической призмы существует связь между углом отклонения лучей от их первоначального направления , показателем преломления стекла n, углом падения лучей на переднюю грань призмы ₁ и двухгранным преломляющим углом призмы А. Используя эту зависимость, получим формулу для определения показателя преломления вещества призмы. Для этого обозначим углы падения луча на грани призмы через ₁ и ₂, а углы преломления луча на этих гранях – через ₁ и ₂. Из геометрических соображений для угла отклонения луча можно записать   ₁  ₂  A.

Для заданного преломляющего угла A угол отклонения оказывается минимальным (  _min), если ход лучей в призме симметричен, то есть если выполняются условия: ₁  ₂ и ₁  ₂  (при этом луч в призме распространяется параллельно основанию). Тогда _min  2₁  A, причём ₁  иsin₁  sin. Подставляя полученные значения ₁ и sin₁ в формулу

n  ,

получаем

n  . (11)

Так как значение показателя преломления зависит от длины волны, то выполнение условия получения минимального угла отклонения для разных длин волн требует различного положения призмы по отношению к падающему пучку лучей. При данном угле падения ₁ существует только одно значение n, удовлетворяющее соотношению (11). Исходя из вышесказанного, для расчёта показателя преломления материала призмы следует измерить угол А при её вершине, а также определить δ_min – минимальные значения угла между подающим на призму и вышедшим из неё лучами света разных длин волн.