физика_1 / 35а

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-2»

Л. М. Касименко, Р. И. Куница

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНОЙ РАБОТЕ 35а

МОСКВА  2009

Работа 35а

ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА

ПО СПЕКТРУ ВОДОРОДА

Цель работы. Изучение спектра водорода.

Приборы и принадлежности: Монохроматор, газосветные трубки с водородом, неоном.

Введение

Спектр испускания возникает при переходе атома из более возбуждённого состояния в менее возбуждённое. Величина испущенного кванта энергии определяется разностью энергетических уровней начального и конечного состояний.

В простейшем случае (атом водорода) сказанное можно проиллюстрировать небольшим расчётом с использованием постулатов Бора и второго закона Ньютона (сила кулоновского притяжения ядром электрона сообщает ему нормальное ускорение).

Постулаты Бора

Первый постулат

Существуют стационарные состоянии, находясь в которых, атом не излучает и не поглощает энергию.

Стационарными являются такие состояния, для которых выполняется условие:

mr  n_iħ (n_i  1, 2, 3,…),

где m – масса электрона,  – скорость электрона, r – радиус его орбиты, ħ  h/(2)  1,0310^34 Дж/с – постоянная Планка.

Второй постулат

При переходе атома из состояния с энергией W_j в состояние с энергией W_i испускается или поглощается один фотон частотой _Ф, энергия которого рассчитывается по формуле

E_Ф  h_Ф  W_j  W_i.

Если W_i  W_j, происходит излучение фотона, если W_i  W_j, – поглощение фотона.

Для атома водорода уравнения, описывающие поведение электрона, имеют вид:

mr  n_iħ, (1)

 . (2)

Решая систему, можно получить значения r и  на соответствующей орбите.

Полная энергия электрона:

W  W_К  W_П    . (3)

Подставив r и  из уравнений (1) – (2) в уравнение (3), получим:

W  .

Отсюда:

_Ф  .

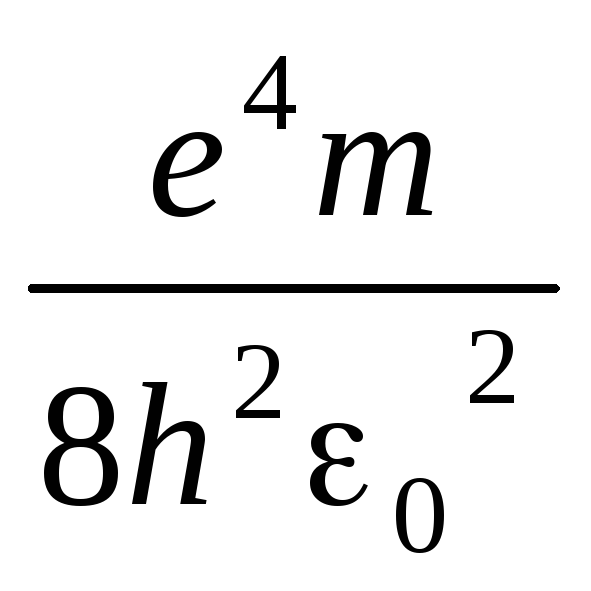
Множитель обозначается буквой R и называется постоянной Ридберга; R  3,2910¹⁵ c^1.

Линейчатые спектры обусловлены испусканием электромагнитного излучения свободными или слабо связанными атомами. Одним из источников такого излучения является возбужденный газ или пар. В данной работе используются газосветные трубки, наполненные водородом и неоном.

Установлено, что спектральные линии атомарного водорода обнаруживают несложные закономерности. Частоты соответствующих линий могут быть определены по формуле

ν  R (4)

где ν – частота, ν  c/, с – скорость света в вакууме, λ – длина волны, R  постоянная Ридберга(R  3,29  10¹⁵ c^1), n_i и n_j – целые числа, причем n_j может принимать значения

(n_i  1),(n_i  2),(n_i  3), ....

Рассмотрим переход атома из различных возбужденных состояний на один и тот же энергетический уровень, определяемый квантовым числом n_i. Совокупность спектральных линий, отвечающая таким переходам, образует серию. В свою очередь, квантовое число n_j определяет энергетический уровень, с которого имел место данный переход, то есть линию в серии.

Различным сериям в спектре атома водорода: (Лаймана, Бальмера, Пашена, Брэккета, Пфунда) отвечают соответственно значения n_i  1, 2, 3, 4, 5.

Рассмотрим, как определить частоты спектральных линий атома водорода, принадлежащих серии Бальмера, для которой n_i  2, n_j  3, 4, 5...,

ν  R (5)

Если приписать n_j значения соответственно 3, 4, 5, 6, то из уравнения (5) получим значения частот спектральных линий, лежащих в видимой области и обозначаемых в спектроскопии H_ H_ H_j, H_. По мере увеличения n_j разность частот соседних линий уменьшается, и при n_j →  сами частоты стремятся к пределу

_ГР  R

где _ГР – частота, соответствующая границе серии Бальмера. У каждой серии есть своя граница, соответствующая ей частота определяется соотношением:

_ГР  R

Рассмотрим физический смысл _ГР. Согласно Бору, при переходе атома с более высокого j-го энергетического уровня на менее высокий i-й уровень излучается квант энергии

hν  E_j  E_i. (6)

Соответственно, чтобы перевести электрон с уровня i на уровень j, необходимо сообщить ему такую же энергию.

Частота ν _ГР определяет энергию (Е  h_ГР), которую надо сообщить электрону, чтобы удалить его с уровня, определяемого числом и, в пространство за пределы атома, где его полная энергия должна быть равна нулю.

Описанный процесс называется процессом ионизации, а Е h_ГР является энергией ионизации атома в данном состоянии.

Эта величина связана с потенциалом ионизации простым соотношением:   h_ГР/e , где e – элементарный заряд, равный 1,610^19 Кл.

Процесс обратный ионизации: захват электрона атомом будет сопровождаться излучением света.

Поскольку электрон, отделенный от атома, может обладать произвольной некоторой кинетической энергией W_К , то при его захвате ионом должна освобождаться энергия (h_ГР  W_К).

Следовательно, согласно второму постулату Бора в этом случае будет испускаться электромагнитное излучение с частотой

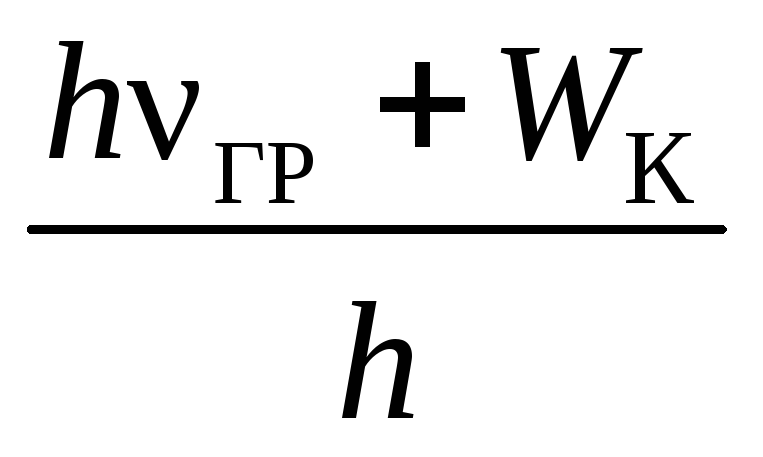
ν   _ГР  .

Таким образом, возможно излучение с частотой, большей нежели частота границы серии, на любую величину W_К/h.

Это означает, что к границе серии со стороны высоких частот прилегает сплошной спектр. Излучение спектров испускания позволяет исследовать строение атома.

Порядок выполнения работы

1. Проградуировать монохроматор по спектру неона (см. лабораторную работу 35). Построить на миллиметровой бумаге градуировочную кривую, то есть график зависимости длины волны от деления на барабане монохроматора.

2. Получить спектр водорода от газосветной трубки. Определить длины волн _i четырех видимых линий спектра водорода по градуировочной кривой.

3. Вычислить частоты, соответствующие данным спектральным линиям по формуле

_i  c/_i

записать значения частоты в таблицу.

4. Рассчитать значения R, используя формулу (5) и полученные в упражнении 3 значения частот (n_j принять равным соответственно 3, 4, 5, 6), записать найденные значения в таблицу.

5. По четырем найдённым из эксперимента значениям R_i определить среднее значение постоянной Ридберга:

R_СР  .

6. Оценить точность измерения, сравнив экспериментально найденное R_СР с теоретическим (R_ТЕОР  3,2910¹⁵ c^1). Относительную ошибку определить по формуле:

100 %.

7. Используя найденные значения частот, по соотношению (6) рассчитать в электрон-вольтах разность энергий между уровнями, соответствующими наблюдаемым переходам для n_j  3, 4, 5, 6 при n  2, учитывая, что h  6,6310^34 Джс – постоянная Планка; с  310⁸ м/с – скорость света в вакууме;1 эВ  1,610^19 Дж.

Таблица

Спектральные линии	nj			R	RСР	Разность энергий между уровнями, эВ
Красная
Голубая
Синяя
Фиолетовая

Приложения (выполняются в рамках УИРС)

Цель приложений – дать возможность студентам расширить круг знаний, получаемых на лекциях. Ознакомление с представленным материалом позволит более осмысленно подойти к выполнению и защите лабораторной работы.

Проанализируем, как действует правило отбора при осуществлении переходов, обусловливающих серию Бальмера, подлежащую изучению в этой работе (рис. 1.).

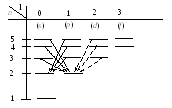
Рис. 1

Серия Бальмера отвечает переходам, заканчивающимся на уровне n  2. Для орбитального квантового числа l имеется правило отбора: ∆l  1. В L-слое (n  2) имеются два электронных состояния 2s и 2p.

В состояние 2s возможны переходы только из np состояния, где n  3, 4, 5… (на рис. 1 переходы указаны сплошными стрелками): np → 2s.

В состояние 2p возможны переходы из ns и nd состояний, где n  3, 4, 5… (на рис. 1 переходы указаны пунктирными стрелками): ns → 2p, nd → 2p.

Совокупность линий, обусловленных указанными переходами, образует серию Бальмера.

Контрольные вопросы

1. Сформулируйте постулаты Бора.

2. Рассчитайте по теории Бора радиус первой орбиты атома водорода.

3. Рассчитайте энергию атома водорода по теории Бора в основном состоянии (n  1).

4. Что определяют в формуле (4) квантовые числа n_i и n_j?

5. Объясните закономерности в спектре атома водорода.

6. Что называется серией?

7. Что такое граница серии?

8. Что называется потенциалом ионизации? Как он определяется?

Список литературы

1. Курс физики: Учеб. пособие для студ. вузов. / А.А. Детлаф, Б.М. Яворский. 7-е изд., стер. – М.: Издат. центр «Академия», 2008. – 720 с.

2. Курс физики: Учеб. для вузов / Т.И. Трофимова. – 7-е изд., стер. – М.: Высшая шк., 2003. – 542 с.

3. Курс общей физики. Кн. 5. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц: Учеб. пособие для втузов. / И.В.Савельев. – М.: ООО «Издательство Астрель». – 2002. – 368 с.