Московский государственный университет

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-2»

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ 31

МОСКВА  2008

Работа 31

ИЗУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

В ДВУХПРОВОДНОЙ ЛИНИИ (СИСТЕМА ЛЕХЕРА)

Цель работы: изучение распределения электромагнитного поля в двухпроводной линии, влияние сопротивления нагрузки на это распределение и определение частоты колебаний электромагнитного поля.

Введение

Электромагнитные волны в двухпроводной линии

бесконечной длины

Если в некоторой области свободного пространства возбудить переменное электрическое поле, то, согласно теории Максвелла, в этой области возникает переменное магнитное поле, в свою очередь порождающее переменное вихревое электрическое поле, и т.д. Эти взаимосвязанные электрические и магнитные поля образуют единое электромагнитное поле, распространяющееся, как это следует из теории Максвелла, со скоростью :

  (1)

где c   310⁸ м/с, ₀ и ₀ – диэлектрическая и магнитная постоянные;  и  –диэлектрическая и магнитная проницаемости среды; n  c/  – показатель преломления среды.

От способа возбуждения электромагнитных волн зависит форма волнового фронта и волновых поверхностей. В простейшем случае, когда волновой фронт – плоскость, и волна распространяется в одном направлении, совпадающем, например, с положительным направлением оси OX выбранной системы координат в однородной, электронейтральной и непроводящей среде, ее можно описать системой уравнений

, (2)

где   2f – угловая (циклическая) частота; f – частота колебаний; k  – волновое число;  – длина волны; x – координата точки, в которой в момент времени t определяется поле.

Уравнения вида (2) называются уравнениями бегущей электромагнитной волны. В этой волне векторы ,иобразуют правую тройку векторов (рис. 1а). Распределение электрических и магнитных полей для фиксированного момента времени в распространяющейся плоской электромагнитной волне приведено на рис. 1б.

В теории электромагнитного поля доказывается, что структура плоской волны не изменится, если в свободном пространстве, в котором она распространяется, поместить две идеально проводящие плоскости, параллельные друг другу и направлению распространения волны и перпендикулярные вектору . Поле между плоскостями останется таким же поперечным, как и в свободном пространстве (рис. 2а). Произведем деформацию этих плоскостей так, как показано на рис. 2б и в, т. е. перпендикулярени, аперпендикулярени. В результате плоскости обратятся в бесконечные цилиндры, а поперечный характер электромагнитного поля при этом сохраняется.

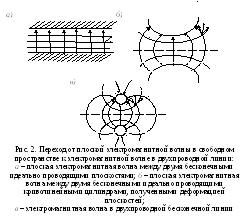
Система двух параллельных проводящих цилиндров образует двухпроводную линию. Электромагнитные волны, возбуждаемые в двухпроводной линии, совпадающей с осью OХ, будут иметь и, лежащие в плоскостиYZ, причем в любой точке этой плоскости векторы ,иобразуют правую тройку векторов. В проводах линии возникают переменные токи проводимости, которые замыкают линии токов смещения, совпадающих с линиямиэлектромагнитного поля, существующего в пространстве вне проводов. Токи проводимости в длинных линиях зависят не только от времени, но и от координат точек линии. Величина тока проводимости в проводниках линии и величина напряжения между проводниками линии в каком-либо сечении могут быть заданы уравнениями, описывающими возникающие в линии волны тока и напряжения, аналогичными формулам (2).

Электромагнитная волна, существующая в двухпроводной линии, так же, как и плоская электромагнитная волна в свободном пространстве, переносит энергию. Величиной, характеризующей плотность потока энергии, переносимой электромагнитной волной, служит вектор Умова-Пойнтинга :

(3)

Для электромагнитной волны в бесконечной двухпроводной линии можно ввести отношение разности потенциалов между проводами линии к величине тока в проводах линии. Это отношение называется волновым сопротивлением линии :

 , (4)

где L₀ и C₀ – индуктивность и емкость отрезка двухпроводной линии единичной длины; U_max и L_max – амплитуды напряжения и тока в линии.