Фгб оу впо

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ»

Кафедра «Физика»

С.М. Кокин, И.А. Лямзова

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО И ФИЗИЧЕСКОГО МАЯТНИКОВ

Методические указания к лабораторной работе № 64 по физике

МОСКВА  2012

ФГБ ОУ ВПО

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ»

Кафедра «Физика»

С.М. Кокин, И.А. Лямзова

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО И ФИЗИЧЕСКОГО

МАЯТНИКОВ

Рекомендовано редакционно-издательским советом университета в качестве методических указаний для студентов ИУИТ, ИПСС и ИТТСУ

МОСКВА 2012

УДК 530.1 (076)

К-55

Кокин С.М., Лямзова И.А. Определение ускорения свободного падения с помощью математического и физического маятников. Методические указания к лабораторной работе № 64 по физике. – М.: МИИТ, 2012. – 16 с.

Методические указания к лабораторной работе № 64 соответствуют программе и учебным планам по курсу общей физики (раздел «Колебания и волны»).

Методические указания предназначены для студентов ИУИТ, ИПСС и ИТТСУ.

© ФГБ ОУ ВПО

«Московский государственный

университет путей сообщения»,

2012

Работа 64

Определение ускорения свободного падения с помощью математического и физического маятников

Цель работы. Изучение свободных незатухающих гармонических колебаний на примере математического и физического маятников; измерение ускорения свободного падения.

Приборы и принадлежности: лабораторный стенд с математическим и физическим маятниками, оптоэлектронный датчик, подключённый к компьютеру, измерительная линейка.

Введение

В настоящей работе свободные незатухающие гармонические колебания изучаются на примере математического и физического маятников¹.

Математический маятник – это материальная точка, подвешенная не невесомой нерастяжимой нити, совершающая малые колебания под действием силы тяжести около положения равновесия. В настоящей работе роль материальной точки исполняет металлический шарик, размеры которого много меньше длины нити (возможное удлинение нити при движении шарика также пренебрежимо мало по сравнению с её длиной). Масса нити намного меньше массы шарика.

Физический маятник – твёрдое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести. В настоящей работе используется оборотный физический маятник, способный колебаться относительно одной из двух осей (в зависимости от способа подвеса).

Процессы, происходящие с выведенными из состояния равновесия математическим и физическим маятниками, опишем с помощью основного закона динамики вращательного движения. Для этого рассмотрим моменты всех сил, действующих на маятники.

На математический маятник (рис. 1а) действуют: сила тяжести и сила натяжения нити , однако вращающий момент создаёт только

сила тяжести. На физический маятник (рис. 1б) также действуют две силы: и сила реакции опоры , но вращающий момент тоже создаёт только сила тяжести².

Таким образом, учитывая, что масса и размеры маятников в процессе колебаний не меняются, формулы основного закона динамики вращательного движения для обоих маятников можно записать в одинаковом виде:

I, (1)

где – момент силы тяжести,I – момент инерции маятника относительно оси вращения (она проходит через точку подвеса: относительно неё и происходят колебания), – угловое ускорение маятника.

Радиус-вектором, соединяющим ось вращения с точкой приложения силы тяжести, в случае математического маятника является вектор , по величине равный длине нити, а в случае физического маятника – вектор , длина которого равна расстоянию от оси вращения до центра тяжести маятника. Если учесть, что момент инерции математического маятника (материальной точки) относительно этой же оси, согласно определению, вычисляется, какI  ml_М², то (см. рис. 1):

• для математического маятника

[]  ml_М², (2)

где │[]│  l_Мmgsin;

• для физического маятника

[]  I, (3)

где │[]│  dmgsin.

Вектор углового ускорения направлен туда же, куда и вектор момента силы тяжести , то есть, как и всеаксиальные вектора, вдоль оси вращения (на рис. 1а – вдоль оси X, на рис. 1б – на нас). Углу отклонения соответствует вектор , такой, что ││ , он всегда направлен в сторону, противоположную и , так как момент силы тяжести всегда стремится уменьшить угол отклонения маятника. Учитывая антипараллельность векторов и , формулы (2) и (3) можно переписать для их проекций:

• для математического маятника: l_Мmg  ml_М², или, с учётом того, что, по определению,   ,

 0; (4)

• для физического маятника dmg  I, или, с учётом того, что, по определению,   ,

 0. (5)

Очевидно, что полученные дифференциальные уравнения имеют решение одного и того же вида, описывающее собственные незатухающие колебания. Для этого достаточно обозначить множитель, стоящий перед вторым слагаемым, символом ₀², и тогда (в этом можно убедиться простой подстановкой) решение приобретает вид:

  Asin(₀t  ), (6)

где A – максимальное значение угла  отклонения (амплитуда), которое должно быть достаточно малым (A  5  8), ₀t   – фаза колебания (измеряется в радианах),  – начальная фаза (фаза в момент времени t  0), ₀ – циклическая частота колебаний, измеряется в радианах в секунду (₀  2, где  – линейная частота колебаний, которая измеряется в герцах, 1 Гц  1 с^1). Согласно формуле (4) для математического маятника

₀  , (7)

а для физического маятника, согласно формуле (5),

₀  , (8)

Но поскольку циклическая частота связана с периодом колебаний соотношением

  , (9)

то это означает, что период колебаний математического маятника

T_М  2, (10)

а период колебаний физического маятника

T_Ф  2. (11)

Формулы (10) и (11), позволяют вычислить значение ускорения свободного падения g, если известны T_М и l или T_Ф, m, d, I:

g  , (12)

или

g  , (13)

Н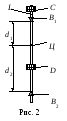о если измерить параметры математического маятникаT_М и l на практике достаточно легко, то воспользоваться для определения ускорения свободного падения формулой (13) совсем не так просто, поскольку для этого необходимо знать достаточно точные значения момента инерции I и массы m физического маятника, а также положение его центра тяжести (расстояние d). Однако существует устройство, называемое оборотным физическим маятником, при использовании которого задача определения g сводится к измерению всего лишь двух параметров: периода колебаний T_ОБ и некоторого расстояния l_ОБ между элементами конструкции этого маятника.

Оборотный маятник устроен следующим образом (рис. 2). На стержне L закрепляются два груза C и D. Маятник снабжён двумя призмами B₁ и B₂, изготовленными из твёрдого материала и расположенными по обе стороны от центра тяжести (точки Ц) системы. При подвешивании маятника с опорой на вершину одной или другой призмы, он приобретает возможность совершать колебания.

Положение грузов C и D регулируется таким образом, чтобы период колебаний маятника при установке на одной призме равнялся периоду его колебаний на другой призме.

Выведем формулу для расчёта периода колебаний оборотного маятника. Согласно теореме Штейнера момент инерции I тела относительно произвольной оси равен сумме момента инерции I₀ этого тела относительно оси, параллельной данной и проходящей через его центр масс и произведения m массы тела на квадрат расстояния d между этими осями:

I  I₀  md². (14)

Если маятник, изображённый на рис. 2, подвесить на призме B₁, то, согласно формулам (11) и (14)³, период его малых колебаний окажется равным

T₁  2. (15)

При подвешивании на призме B₂ период колебаний описывается формулой

T₂  2. (16)

Но поскольку грузы расположены так, что T₁  T₂, то