Равновесие и остойчивость тел, погруженных в жидкость

1. Закон Архимеда

Определим силу давления жидкости на погруженное тело А объемом W (рис. 12). Представим себе, что в жидкости выделен объем точно такой же, как и тело А. Этот объем жидкости находится в равновесии под действием только двух сил:

1) силы давления жидкости p на поверхность выделенного объема 2) силы тяжести жидкости, равной ρWg и направленной вертикально вниз.

Рис.12

Следовательно, сила Р по вели­чине равна силе тяжести выделенного объема жидкости, направлена в обрат­ную сторону, т.е. вертикально вверх, и приложена в центре D объема (рис.12), т.е. в той же точке, в ко­торой приложена сила тяжести выде­ленного объема жидкости. Точка D называется центром водоизмещения.

Таким образом, сила давления жидкости на погружен­ное в нее тело приложена в центре водоизмещения, напра­влена вертикально вверх и равна силе тяжести, жидкости в объеме, вытесняемом телом (закон Архимеда);

Сила Р называется архимедовой силой, W - объемным водоизмещением, а про­изведение ρW - водоизмещением.

2. Равновесие и остойчивость тел, полностью погруженных в жидкость. Условия равновесия

Если сила тяжести G тела А (рис. 12) больше архиме­довой силы Р, то равнодействующая этих двух сил (Р и G) направлена вниз и заставляет тело опускаться на дно. Таким образом, если Р < G, тело тонет.

Если сила тяжести G тела А меньше архимедовой силы Р, то равнодействующая этих двух сил (Р и G) на­правлена вверх и заставляет тело подняться на поверх­ность. При выходе части тела из жидкости сила давления на оставшуюся погруженную часть тела соответственно уменьшается, благодаря чему уменьшается и величина направленной вверх равнодействующей, заставляющей тело всплывать; в результате при некотором частич­ном погружении тела устанавливается равновесие и тело оказывается плавающим на поверхности жид­кости. Таким образом, если Р > G, тело всплывает на по­верхность жидкости.

Для того чтобы тело А (рис. 12) не опускалось на дно и не всплывало, необходимо, чтобы Р = G.

Архимедова сила Р = ρWg, а сила тяжести тела G =m g; следовательно, для равновесия тела должно быть ρWg = mg. Сокращая на g, получаем

(28)

т. е. для равновесия необходимо, чтобы водоизмещение равнялось массе т плавающего тела.

Это условие будет достаточным лишь в том случае, когда С - центр тяжести тела и D - центр водоизмеще­ния совпадают. В общем случае центр тяжести С и центр водоизмещения D могут и не совпадать (рис. 13). Тогда тело, несмотря на выполнение условия , в равно­весии может и не находиться (рис. 13б), так как имеется пара, вращающая тело. Как видно из рис. 13а, враще­ние прекратится, когда прямая, проходящая через центр тяжести С и центр водоизмещения D, так называемая ось плавания, станет вертикальной.

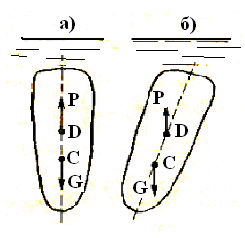
Рис.13.

Итак, имеются два условия равновесия тел, полностью погруженных в жидкость:

1. ;

2. ось плавания должна быть вертикальна.

Условия остойчивости

Рассмотрим условия остойчивости, т. е. способности плавающего тела возвращаться в первоначальное положе­ние равновесия после прекращения действия силы, вызвав­шей крен.

Возможны три случая:

1) центр тяжести С лежит ниже центра водоизмещения D (рис. 13, а);

1. центр тяжести С находится выше центра водоизмещения D (рис. 14, а);

Рис.14

3) центр тяжести С совпадает с центром водо­измещения D (рис.15, а).

В первом случае равно­весие остойчивое, так как при крене возникает пара (рис. 13, б), стремящаяся вернуть тело в первона­чальное положение равно­весия.

Во втором случае рав­новесие неостойчивое, так как при крене возникает пара (рис. 14, б), стремящаяся еще более отклонить тело от положения равновесия.

В третьем случае равновесие безразличное, так как тело будет находиться в равновесии при любом положении (рис. 15б).

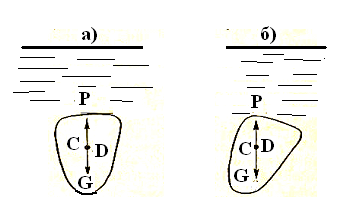
Рис.15.

ГЛАВА ЧЕТВЕРТАЯ